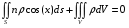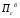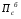Проектирование хим. предприятий. Навчальний посібник до вивчення курсу основи проектування хімічних виробництв
 Скачать 6.93 Mb. Скачать 6.93 Mb.
|
|
Глава 7 УРАВНЕНИЯ МАТЕРИАЛЬНОГО БАЛАНСА ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА 7.1. СТЕХИОМЕТРИЧЕСКИЕ РАСЧЕТЫ Все количественные соотношения при расчете химических процессов основаны на стехиометрии реакций. Количество вещества при таких расчетах удобнее выражать в молях, или производных единицах (кмоль, ммоль, и т.д.). Моль является одной из основных единиц СИ. Один моль любого вещества соответствует его количеству, численно равному молекулярной массе. Поэтому молекулярную массу в этом случае следует считать величиной размерной с единицами: г/моль, кг/кмоль, кг/моль. Так, например, молекулярная масса азота 28 г/моль, 28 кг/кмоль, но 0,028 кг/моль. Массовые и мольные количества вещества связаны известными соотношениями NА = mА/МА; mА = NА МА, где NА - количество компонента А, моль; mA - масса этого компонента, кг; МА - молекулярная масса компонента А, кг/моль. При непрерывных процессах поток вещества А можно выражать его моль- ным количеством в единицу времени WA = NA/τ, где WA — мольный поток компонента А, моль/с; τ — время, с. Для простой реакции, протекающей практически необратимо, обычно стехиомет рическое уравнение записывается в виде vAА + vBВ = vRR + vSS. Однако удобнее записывать стехиометрическое уравнение в виде алгебраическо го, принимая при этом, что стехиометрические коэффициенты реагентов отрицательны, а продуктов реакции положительны: Тогда для каждой простой реакции можно записать следующие равенства: 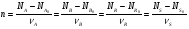 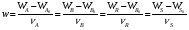 Индекс «0» относится к начальному количеству компонента. Эти равенства дают основание получить следующие уравнения материального баланса по компоненту для простой реакции: 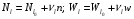 Пример 7.1. Реакция гидрирования фенола до циклогексанола протекает по урав- нению С6Н5ОН + ЗН2 = С6Н11ОН, или А + ЗВ = R. Вычислить количество образовавшегося продукта, если начальное количество компонента А было 235 кг, а конечное - 18,8 кг Решение: Запишем реакцию в виде R - А - ЗВ = 0. Молекулярные массы компонентов: МА = 94 кг/кмоль, МВ = 2 кг/кмоль и МR = 100 кг/кмоль. Тогда мольные количества фенола в начале и в конце реакции будут: NA0 = 235/94 = 2,5; NA0 = 18,8/94 =0,2; n = (0,2 - 2,5)/(-1) = 2,3. Количество образовавшегося циклогексанола будет равно NR = 0 +1∙2,3 = 2,3 кмоль или mR = 100∙2,3 = 230 кг. Определение стехиометрически независимых реакций в их системе при материальных и тепловых расчётах реакционных аппаратов необходимо для исключения реакций, являющихся суммой или разностью некоторых из них. Такую оценку наиболее просто можно осуществить по критерию Грама. Чтобы не проводить излишних расчетов, следует оценить, является ли система стехиометрически зависимой. Для этих целей необходимо: - транспонировать исходную матрицу системы реакций; - умножить исходную матрицу на транспонированную; - вычислить определитель полученной квадратной матрицы. Если этот определитель равен нулю, то система реакций стехиометрически зависима. Пример 7.2. Имеем систему реакций: FеО + Н2 = Fе + Н2O; Fе2О3+ 3Н2 = 2Fе + 3Н2O; FеО + Fе2O3 + 4Н2 = 3Fе + 4Н2O. Эта система стехиометрически зависима, так как третья реакция является суммой двух других. Составим матрицу
Определитель равен нулю. При отбрасывании третьей реакции определитель равен 28, т.е. две первых реакции стехиометрически независимы.  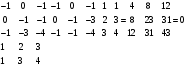 Для удаления стехиометрически зависимых реакций в системе необходимо составить матрицу системы. Допустим для системы реакций: 4NН3 + 5О2 = 4NО + 6Н2O; 4NH3+ 3О2 = 6Н2O + 2N2; 4NН3 + 6Н2O = 5N2+ 6Н2O; O2 + 2NO = 2NO2; 2NO = O2 + N2; 2O2 + N2 = 2NO2, можно составить матрицу:
По сути, к данной матрице следует применить преобразование Гаусса. Заменим вторую и третью строку их разностями с первой и умножим на 2, разделим на 5 третью строку, которую вычтем из второй. Затем умножим четвертую и пятую строку на 2 и вычтем их из второй:
Умножим пятую строку на - 2 и вычтем ее из второй, а также вычтем из второй строки шестую. Умножив затем шестую строку на 2 и вычитая ее из четвертой, получим окончательно
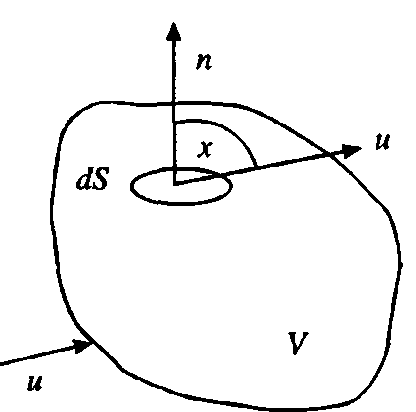
Отсюда видно, что третья, пятая и шестая реакции являются стехиометрически зависимыми. Окончательно система примет вид, если для простоты расчетов подставить вместо полученной четвертой реакции ее разность со второй 4NH3 + 5O2 = 4NO + 6Н2O; 2NO = N2 + O2; 2NО + О2 = 2NO2 Одновременно с числом стехиометрически независимых реакций определяется равное ему число ключевых веществ, по которым можно составить материальный баланс реакций. В простой реакции основное вещество одно. В сложных реакциях выбор независимых реакций и основных веществ взаимосвязан и определяется тем, чтобы в каждой независимой реакции участвовало хотя бы одно основное вещество и, кроме того, выбранные основные вещества участвовали бы в одной или в некотором минимуме реакций. Так, в предыдущем примере в качестве основных можно выбрать аммиак, азот и диоксид азота. Для каждой из независимых реакций можно записать: 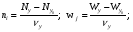 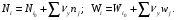 Здесь i - индекс, соответствующий веществу, j - индекс, соответствующий номеру реакции. 7.2. ОБЩЕЕ УРАВНЕНИЕ БАЛАНСА МАССЫ В расчетах процессов химической технологии обычно используется система координат Эйлера, т.е. система координат, фиксированная относительно некоторого неподвижного объема пространства, через который протекает материальная среда. Такой объем называют контрольным, а поверхность, ограничивающую контрольный объем, именуют контрольной. Выделим на контрольной поверхности S элементарную площадку dS и восста новим к ней нормаль n (см. рис. 7.1).
расход вещества через контрольную поверхность, а второй - скорость накопления вещества в контрольном объёме. Для химических аппаратов можно полагать, что вектор скорости потока перпендикулярен контрольной поверхности в точках входа и выхода и параллелен ей в остальных точках, поэтому это уравнение можно проинтегрировать: 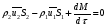 Два первых слагаемых в уравнении есть разность потоков на выходе и входе в аппарат, а третье - скорость накопления вещества в аппарате. Средняя скорость потока 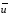 определяется выражением (по теореме о среднем) определяется выражением (по теореме о среднем)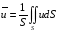 Если определить массовый расход как 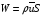 , то предпоследнее уравнение при- , то предпоследнее уравнение при-мет вид 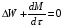 Для стационарного процесса 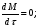 ∆W = 0; W1 = W2; ∆W = 0; W1 = W2;Все эти уравнения являются балансом массы по всему веществу, проходящему че- рез контрольный объем. Уравнение баланса массы по компоненту в такой же фор- ме можно записать так: 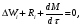 где Ri - скорость образования или расходования компонента i за счет химической реакции. Последнее уравнение получено в предположении отсутствия диффузионных потоков. Его можно записать для каждого компонента системы. В сумме они дадут уравнение баланса массы по всему веществу, так как 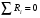 . .Таким образом, для n-компонентной системы можно составить n уравнений, причем одно уравнение общего баланса массы и (n - 1) уравнение балансов массы по компонентам смеси. При отсутствии химических реакций уравнение общего баланса массы можно записать в мольных расходах: 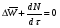 При наличии химического взаимодействия уравнение в мольных расходах по ком- поненту примет вид 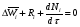 где Ni — число молей компонента. Суммирование последнего уравнения по всем компонентам дает 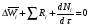 В обшем случае сумма скоростей превращения компонентов 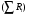 не всегда равна нулю, так как число молей в процессе реакции может изменяться. Рассмотрим пример применения уравнения материального баланса к нестационарному процессу не всегда равна нулю, так как число молей в процессе реакции может изменяться. Рассмотрим пример применения уравнения материального баланса к нестационарному процессуПример 7.3. При упрощенном способе производства Н3РO4 в хорошо перемешива- емую емкость, где реагирует 4000 кг/ч взвешенного в воде Са3(РO4)2, подается стехиометрическое количество 94%-ной серной кислоты. Вместе с фосфоритной мукой подается вода в количестве, достаточном для получения при стационарном ходе процесса 40%-ной фосфорной кислоты. Образующиеся раствор фосфорной кислоты и гипс (СаSO4∙2Н2O) равномерно удаляются из смесителя так что общая масса в нем остается постоянной. Какова будет концентрация раствора фосфорной кислоты в емкости по истечении 1 часа работы, если процесс начался, когда в емкости находилось 4000 кг 20%-ной фосфорной кислоты? Решение: Запишем уравнение реакции и проведем стехиометрические расчеты в предположении полного превращения фосфорита: Са3(РO4)2 + 3Н2SO4 + 6Н2O = 2Н3РO4 + 3(СаSO4∙2Н2О). Или в буквенном выражении: - А - 3С - 6В + 2F + 3G = 0. Молекулярные массы компонентов реакции в кг/кмоль: MA = 310,18; MC = 98,07; МB = 18,02; МF = 98,00; МG = 172,17. Определим коэффициент расхода по фосфориту 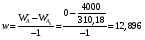 Тогда расходы компонентов будут равны (кг/ч): WC0=WC – w (-3) MC = 0- 12,896 ∙ (-3) 98,07 = 3794,1; WB0= 0 - 12,896 ∙ (-6) 18, 02 = 1394, 3; WF = WF0 + 2МF = 0 + 12,896 ∙2 ∙98, 00 = 2527, 6; WC = 0+ 12,896 ∙3 ∙172, 17 = 6660, 92. Определим количество воды, подаваемой с фосфоритной мукой. Составим баланс по воде 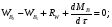 По условию задачи dMB/dτ = 0. Расход воды, уходяшей с фосфорной кислотой 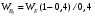 = 2527,6 ∙(1 - 0,4)/0,4= 3791,4 кг/ч. = 2527,6 ∙(1 - 0,4)/0,4= 3791,4 кг/ч. Расход воды, приносимой с серной кислотой 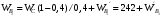 ,кг/ч. ,кг/ч. Скорость образования воды по химической реакции RW =WB0 = 1394, 3 кг/ч. Тогда расход воды, подаваемой с фосфоритной мукой 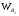 = 3791,4 + 1394,3 - 242 = 4943,7 кг/ч. = 3791,4 + 1394,3 - 242 = 4943,7 кг/ч. Составим баланс по фосфорной кислоте: 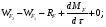 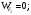 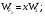 RF = WF = 2527, 6 кг/ч RF = WF = 2527, 6 кг/ч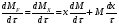 где х - концентрация фосфорной кислоты на выходе из емкости и в самой емкости; М - общее количество реакционной смеси, кг. 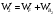 = 2527,6 + 3791,4 = 6319 кг/ч. = 2527,6 + 3791,4 = 6319 кг/ч.Для определения общего количества реакционной смеси (М) составим уравнение баланса по всему веществу: 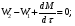 W2 = W1; dM/dτ = 0; dM = 0; M = M0 W2 = W1; dM/dτ = 0; dM = 0; M = M0где М0 — начальное количество вещества в емкости; М0 = 4000 кг. Тогда 6319х - 2527,6 + 4000 (dx/dτ) = 0. После разделения переменных 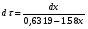 Проинтегрируем полученное уравнение в пределах от 0 до τ и от 0,2 до х. После преобразований получим х=0,4 - 0,2ехр(-1,580τ). За время 1 час концентрация фосфорной кислоты станет равной х = 0,4 - 0,2ехр(-1,580) = 0,3588 или 35,88%. Проверка физического смысла полученного решения дает: при τ → ∞ х → 0,4. 7.3. ПРАКТИЧЕСКИЙ МАТЕРИАЛЬНЫЙ БАЛАНС Практический материальный баланс учитывает составы исходного сырья и готовой продукции, избыток одного из компонентов сырья, степень превращения реагентов, потери сырья и готового продукта и т.д. Исходными данными для составления такого баланса являются: - технологическая схема, отражающая вид и последовательность стадий производства; - годовая производительность по данному продукту или данному спектру продуктов; - производственная рецептура загрузки компонентов на каждой технологической стадии; - потери сырья и готового продукта на каждой технологической стадии производства. В зависимости от характера требований материальный баланс периодичес ких процессов может составляться в трех вариантах: во-первых, исходя из суточной производительности вещества; во-вторых, на единицу массы готового продукта (чаще всего на 1 т); в-третьих, на количество готового продукта, полученного за один цикл работы. В этом случае наиболее целесообразен суточный материальный баланс. Для непрерывных процессов материальный баланс составляется с учетом выработки в единицу времени (т/год, т/сут, т/ч, кг/ч, кг/мин, кг/с и т.д.). В любом случае баланс делится на две основные части - общий материальный баланс и пооперационный (постадийный) материальный баланс. При общем балансе материальные расчеты связаны с определением расхо дов всех видов сырья. В большинстве случаев такие расчеты завершаются определением расходных коэффициентов всех компонентов процесса на единицу массы готового продукта (например, на 1 т) и сравнением их с расходными коэффициентами аналогичного существующего производства. Первым этапом будет определение рабочего времени в цехе. Его величина зависит от характера производства. Для периодических процессов Д = 365 - (Р + В), где Д - количество рабочих дней в году; Р - количество дней в году, отведенных на все виды ремонта; В - количество праздничных и выходных дней в году. Для непрерывных процессов Д = 365 - Р. В этом случае величина Р включает в себя и время на все виды ремонтов, и время периодических остановок на чистку оборудования, замену катализатора и т. п. Далее необходимо определить производительность по готовому продукту. Вначале рассчитывается производительность без учета потерь 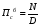 где 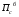 - суточная производительность по готовому продукту без учета потерь, т/сут; N - годовой выход готового продукта, т. - суточная производительность по готовому продукту без учета потерь, т/сут; N - годовой выход готового продукта, т.Производительность с учетом потерь продукта по стадиям 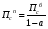 где а - общая доля потерь продукта на всех стадиях процесса. Общая величина потерь по всем стадиям 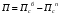 Определяя доли потерь по стадиям как аi можем найти их количество из соотно- шения 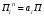 При этом 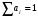 Далее определяется расход каждого вида сырья с учетом потерь, исходя из рецептуры загрузки компонентов реакционной смеси. При этом предварительно рассчитывается рецептура в процентах на содержание каждого компонента, полагая за 100% всю реакционную смесь. Потери реакционной смеси на каждой стадии в равной степени относятся к каждому из компонентов, если нет отгона одного из продуктов, выделения его в осадок и др. К полученным расходам сырьевых компонентов добавляются их возмож- ные потери до получения реакционной смеси при транспортировке, загрузке и т.д. Окончательно производят расчет расходных коэффициентов сырьевых ком- понентов на тонну готового продукта. Результаты расчета расходных коэффициентов оформляются в виде таблицы (см. таблицу 7.1) Таблица 7.1. Пример представления расходных коэффициентов
Кроме расходных коэффициентов сырья рассчитываются аналогичные величины, характеризующие расход воды, пара, топлива, электроэнергии и т.д. Естественно, чем меньше расходные коэффициенты, тем экономичнее технологический процесс. Особое значение имеют расходные коэффициенты по сырью, так как для большин- ства химических производств львиная доля себестоимости продуктов приходится на эту статью. Постадийный материальный баланс составляется в виде таблиц на каждой стадии, исходя из результатов расчета общего материального баланса. Пример 7.4. Составить материальный баланс реактора каталитического окисления метанола в формальдегид. Производительность реактора по формальдегиду 10 000 т/год. Степень превращения метанола в формальдегид - 0,7; общая степень превращения метанола (с учетом побочных реакций) - 0,8. Содержание метанола в спирто-воздушной смеси - 40% по объему. Мольные соотношения побочных продуктов на выходе из реактора НСООН : СО2: СО : СН4 = 1,8 : 1,6 : 0,1 : 0,3. Аппарат работает 341 день в году с учетом времени ППР (планово-предупреди- тельных ремонтов) и простоев. Решение: Формальдегид получается в результате окисления паров метанола кислородом воздуха при температуре 550 - 600 °С на серебряном катализаторе, где протекают следующие реакции:
Возможная реакция Н2 + 1/2О2 = Н2О стехиометрически зависима, так как она в сумме с реакцией (2) дает реакцию (1), поэтому ее нужно из балансовых расчетов исключить. На реакцию подается лишь около 80% воздуха от мольного соотношения метанол : кислород = 2 : 1 и процесс проводится с неполным сгоранием водорода, образую- щегося по реакции (3). Отходящие газы содержат 20 - 21% формальдегида, 36 - 38% азота и примеси в ви- де СО, СО2, СН4, СН3ОН, НСООН и др. Вся эта смесь после охлаждения в котле-утилизаторе и холодильнике до 60 °С подается в поглотительную башню, оро- шаемую водой. Полученный раствор формалина содержит 10 - 12% метанола, который в данном случае является желательной примесью, так как препятствует по- лимеризации формальдегида. Молекулярные массы: формалина - 30; метанола - 32; кислорода - 16. Производительность реактора по формальдегиду 10 000∙1000/341/24 = 1222 кг/ч или 1222/30 = 40,73 кмоль/ч. Так как по реакциям (1) и (2) на образование 1 моля формальдегида расходуется 1 моль метанола, то, при 70% степени превращения метанола в формальдегид, имеем расход метанола: 40,7/0,7 = 58,143 кмоль/ч или 58,143 ∙32= 1860,6 кг/ч. Определим объемные расходы исходных веществ при нормальных условиях. Метанол - 58,143 ∙22,4= 1302,4 м3/ч. Спирто-воздушная смесь - 1302,4/0,4 = 3256 м3/ч. Воздух - 3256 – 1302,4 = 1953,6 м3/ч, в нем: кислорода – 1953,6 ∙0,21 = 410,26 м3/ч или 410,26 ∙32/22,4 = 586 кг/ч; азота – 1953,6 ∙0,79 = 1543 м3/ч или 1543 ∙28/22,4 = 1929 кг/ч. Определим расход метанола, пошедшего на образование побочных продуктов по реакциям (3) - (6). При общей степени превращения метанола 80% имеем расход метанола по побочным реакциям 58,143 ∙(0,8 - 0,7) = 5,81 кмоль/ч. Не прореагировало метанола 58,143∙ 0,2 = 11,63 кмоль/ч или 11,63∙32 = 372 кг/ч. Сумма долей побочных продуктов 1,8+ 1,6 + 0,1 + 0,3 = 3,8. Тогда расходы побочных продуктов в отходящих газах будут равны: Уксусная кислота (НСООН) - 5,8∙1,8/3,8 = 2,75 кмоль/ч или 2,75∙46 = 126,5 кг/ч. Диоксид углерода (СО2) - 5,8∙1,6/3,8 = 2,45 кмоль/ч или 2,45∙44 = 108,0 кг/ч. Оксид углерода (СО) - 5,8∙0,1/3,8 = 0,158 кмоль/ч или 0,158∙28 = 4,3 кг/ч. Метан (СН4) - 5,8∙0,3/3,8 = 0,459 кмоль/ч или 0,459∙16 = 7,3 кг/ч. Для определения расходов водяного пара и водорода составим баланс по кислороду и водороду. В реактор поступает кислорода: с воздухом - 586 кг/ч; в составе метанола – 1860,6∙16/32 = 930 кг/ч. Всего: 586 + 930 = 1516 кг/ч. Расходуется кислорода: на образование формальдегида -1220∙16/30 = 650 кг/ч; на образование НСООН - 126,5∙32/46 = 88 кг/ч; на образование СО2 - 108∙32/44 = 78,6 кг/ч; на образование СО - 4,3∙16/28 = 2,45 кг/ч; в составе не прореагировавшего метанола - 372 16/32 = 186 кг/ч. Всего: 1005 кг/ч. Остальное количество кислорода, равное 1516 -1005 = 509 кг/ч, пошло на образование воды по реакциям (1), (4), (5) и (6). В результате расход воды равен - 509∙18/16 = 572 кг/ч. В реактор поступает водорода - 1860∙4/32 = 233 кг/ч. Водород расходуется: на образование СН2О - 1220∙22/30 = 81,5 кг/ч; на образование НСООН - 126,5 2/46 = 5,5 кг/ч; на образование СН4 - 7,3∙4/16 = 1,82 кг/ч; на образование Н2О - 572 2/18 = 63,6 кг/ч; в составе не прореагировавшего газа - 372∙4/32 = 46,5 кг/ч. Всего: 198,9 кг/ч. Количество водорода в свободном состоянии: 233 - 198,9 = 34,1 кг/ч. Результаты расчета сведены в табл. 7.2 материального баланса. Таблица 7.2. Материальный баланс процесса получения формальдегида
7.4. ФИЗИКО-ХИМИЧЕСКИЕ ОСНОВЫ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА Основная цель выполнения этого раздела - дать обоснование норм технологического режима в реакторе (концентраций, температуры, давления, степени превращения и т.д.). Для обоснования норм технологического режима привлекаются данные по термодинамике, а также сведения по механизму и кинетике основных и побочных реакций. Термодинамические данные используются для определения области значения параметров, в которой процесс протекает, а также для расчета степеней превращения исходных веществ, если процесс происходит в равновесных условиях. Кинетические данные (константы скоростей химических реакций, константы равновесия, энергии активации реакций) необходимы как при определении норм технологического режима, так и при расчете размеров реакторов. Следует напомнить, что нормы технологического режима определяются как кинетическими, так и технико-экономическими показателями. Так, повышение температуры ведет к увеличению скорости процесса и к повышению производительности единицы объема реактора, но с ростом температуры может, например, уменьшаться селективность процесса, т.е. увеличиваются затраты сырья. Кроме того, верхний предел температуры может определяться и термической устойчивостью перерабатываемых и получаемых веществ, а также свойствами энергоносителей и катализаторов. Давление в аппарате определяется не только исходя из конструкционных зависимостей для скорости процесса или константы равновесия, но и исходя из затрат на создание давления или вакуума, требований техники безопасности и т.п. Например, назначение в аппарате давления меньше атмосферного нецелесообразно там, где перерабатываются огне- или взрывоопасные вещества при температурах выше температур самовоспламенения. Подача воздуха в эти реакторы через фланцевые соединения или при появлении трещин в конструкционном материале за счет эрозии, коррозии и т.п. приводят к взрыву. Целесообразно в этом случае вместо вакуума работать при давлении выше атмосферного или применять инертные разбавители для снижения парциальных давлений перерабатываемых веществ. В аппаратах величина рабочего давления может определяться также гидравлическим сопротивлением в целом. Часто незначительное повышение давления позволяет использовать такие дешевые хладагенты, как промышленная оборотная вода или воздух вместо значительно более дорогого рассола. Назначение степени превращения сырья, а, следовательно, и величина времени контакта определяется, в основном, зависимостью селективности от степени превращения, поэтому стремление к полному превращению сырья может привести иногда к неоправданному увеличению реакционного объема. Концентрации реагентов определяются стремлением достичь не только высоких скоростей процесса, но также обеспечением высокой селективности с учетом кинетических порядков основной и побочных реакций. Выбираемые концентрации могут определяться величинами вязкости растворов, стремлением обеспечить требуемые режимы теплообмена и т.д. Иногда целесообразно для поддержания высоких скоростей процесса и больших степеней превращения поддерживать в реакторе избыток одного из реагентов. Обычно выбирают для этого реагент дешевый и легко выделяемый в дальнейшем на стадии очистки. Такой прием при назначении норм технологического режима позволяет добиться более полного использования дорогого и дефицитного сырья за счет рационального соотношения реагентов в реакторе. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||