Проектирование хим. предприятий. Навчальний посібник до вивчення курсу основи проектування хімічних виробництв
 Скачать 6.93 Mb. Скачать 6.93 Mb.
|
|
Глава 9 ТЕПЛОВОЙ РАСЧЕТ ОСНОВНОГО ОБОРУДОВАНИЯ 9.1. ОБЩЕЕ УРАВНЕНИЕ БАЛАНСА ЭНЕРГИИ Уравнение баланса энергии в интегральной форме может быть получено из первого закона термодинамики 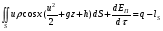 где первое слагаемое в скобках - кинетическая энергия движения жидкости, второе - потенциальная энергия положения, третье -энтальпия жидкости, Дж/кг; Еп - полная энергия в контрольном объеме, Дж; q - тепловой поток через контрольную поверхность, Вт; lS - мощность на преодоление внешних сил, в основном сил трения, Вт; u - скорость потока, м/с; ρ - плотность среды, кг/м3; х - угол между нормалью и контрольной поверхностью; g - ускорение силы тяжести, м/с2; z - геометрический напор, м; h - удельная энтальпия, Дж/кг; S - контрольная поверхность; τ - время, с. Для химических процессов кинетическая и потенциальная энергии, а также мощность на преодоление внешних сил пренебрежимо малы по сравнению с энтальпией, поэтому можно записать 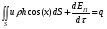 Это уравнение, по сути, является уравнением теплового баланса. Для простого контрольного объема, ограниченного контрольными поверхностями, перпендикулярными вектору потока жидкости, интегрирование последнего уравнения дает 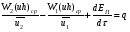 Первые два слагаемых в этом уравнении получены следующим образом. Если принять плотность постоянной, а соs(х) = ±1, то 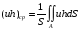 , тогда , тогда 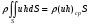 Так как 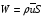 то получаем то получаем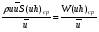 Если скорость незначительно меняется в обоих сечениях, а поток жидкости стационарен в гидродинамическом отношении, то уравнение баланса тепла можно записать следующим образом: 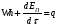 Если система стационарна и в тепловом отношении, то: 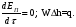 Если в системе не происходит фазовых превращений и химических реакций, то можно от энтальпий перейти к теплоемкостям и тогда 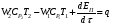 Рассмотрим пример применения уравнений теплового баланса в нестационарных условиях. Пример 9.1. Два резервуара объемом по 3м3 каждый заполнены водой при температуре 25 °С. Оба имеют мешалки, обеспечивающие практически полное перемешивание. В определенный момент времени в первый резервуар начинают подавать 9000 кг/ч воды при температуре 90°С. Вода, выходящая из первого резервуара, поступает во второй. Определить температуру воды во втором резервуаре через 0,5ч после начала подачи горячей воды. Резервуары считать теп- лоизолированными. Решение: Составим схему тепловых потоков (рис. 9.1) и тепловой баланс для первого резервуара. 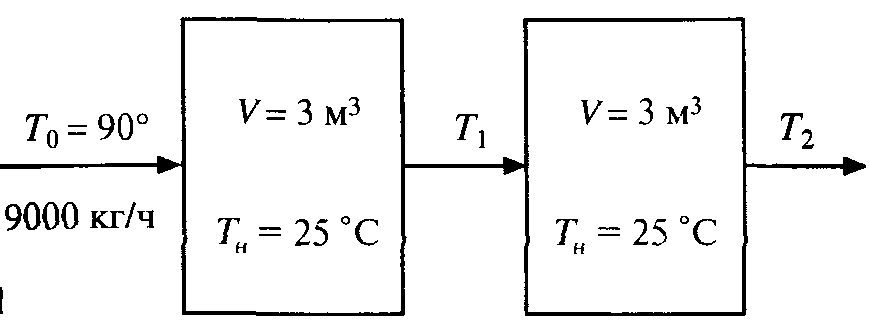 Рис.9.1 Схема тепловых потоков к примеру 9.1 При отсутствии теплообмена q = 0 и при условиях W = W1 = W2; Ср = Ср1 = Ср2; dЕп = VρСPdТ1, уравнение теплового баланса примет вид WCP(T0 – T1)dτ = VρCPdT1 После интегрирования от 0 до τ и от 25°С до Т1, получим Т1 = 90 - 65ехр(-3τ) Составим аналогичным образом тепловой баланс второй емкости WCP(T1 – T2)dτ=VρCPdT2 откуда 9000(T1 - Т2) dτ = 3∙1000 dT2 или 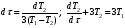 Получено линейное дифференциальное уравнение первого порядка. Его можно проинтегрировать известным способом аналитически. Тогда имеем Т2 = ехр(-3τ)(90 ехр(3τ) - 195τ+ С) Начальные условия: при τ=0 Т2 = 25 °С. Произвольная постоянная С = - 65. Окончательно решение примет вид Т2 = 90 - 65 (3τ +1) ехр(-3τ); T2 = 90 - 65(3∙0,5 + 1)ехр(-3∙0,5) = 53,740С. 9.2. ПРАКТИЧЕСКИЙ ТЕПЛОВОЙ БАЛАНС Практический тепловой баланс в общем случае определяется простым уравнением 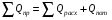 где Qпр - физическое тепло, вносимое в аппарат реагентами, материалом аппарата (для периодических процессов), тепло фазовых переходов, тепло реакции и т.д.; Qрасх - физическое тепло, уносимое из аппарата продуктами реакции; Qпот - тепло, теряемое в окружающую среду. При неизвестных размерах аппарата точное определение величин тепла, теряемого в окружающую среду, невозможно. В этом случае принимают Qпот равным 3-5% от максимального значения суммы вносимого или уносимого тепла. Если геометрические размеры аппарата известны, то можно оценить потери тепла по уравнению теплоотдачи 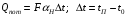 где Qпот - поток потерянного тепла, Вт; F - наружная поверхность теплообмена аппарата, м2; αн - наружный коэффициент теплоотдачи. Вт/(м2∙К); tП - температура наружной поверхности аппарата, 0С; t0 - температура окружающей среды, 0С. Температура наружной поверхности аппарата либо определяется из санитар- ных условий (<50°С), либо задается условиями работы аппарата. Температура ок- ружающей среды выбирается минимальной для данного помещения или района (при установке оборудования на открытом воздухе). Наружный коэффициент теп- лоотдачи рассчитывается по двум составляющим: αн= αк + αл где αк - коэффициент теплоотдачи конвекцией; αл - коэффициент теплоотдачи лучеиспусканием. Конвективный коэффициент теплоотдачи зависит от места установки оборудования и от его положения в пространстве. Горизонтальные трубопроводы и оборудование внутри помещений: при ∆t∙d3 > 9,8∙10 -2 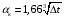 при 9,8∙10-2 ≥ ∆t∙d3>6,5∙10-6 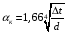 где d - наружный диаметр аппарата. Для вертикальных аппаратов и трубопроводов внутри помещения: 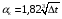 . .При установке оборудования на открытом воздухе: для плоских стенок αк = (5,95 + 1,5∙t0/100)(w0,6/l0,2) где w - скорость ветра, м/с; l - длина стенки по направлению ветра, м; для аппаратов αк = (5,1 + 0,3∙t0/100)(w0,6/d0,4) для горизонтальных трубопроводов αк = 3,9(w0,6/d0,4) Коэффициент теплоотдачи лучеиспусканием (температура в К) 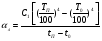 где С1 - степень черноты поверхности аппарата или трубопровода. В случае расчета теплоизоляции аппарата или трубопровода, величина Q будет допустимой потерей тепла в окружающую среду. Тогда толщину слоя теплоизоляции можно рассчитать по формуле 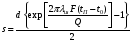 где λиз - коэффициент теплопроводности материала изоляции. Пример 9.2. Определить температуру реакционной смеси процесса окисления метанола до формальдегида на входе в реактор, полагая температуру на выходе из реакционной зоны, равной 800 °С. Результаты материальных расчетов взять из примера 8.3. Теплоемкости компонентов реакции принять средними при температуре 650 °С. Решение: Определим теплоемкости компонентов процесса. Из справочника выпишем стандартные энтальпии образования и температурные зависимости теплоемкостей всех веществ, участвующих в процессе (табл.9.1). Таблица 9.1. Энтальпии образования и температурные зависимости теплоемкости
Для всех реакций процесса рассчитаем энтальпию реакции, кДж/моль реакция (1) - 115,9 - 241,84 + 201,2 + 0,5 0 = -156,54; реакция (2) - 115,9 - 0 + 201,2 = 85,3; реакция (3) - 110,5 -2 0 + 201,2 = 126,35, реакция (4) - 74,85 - 241,84 + 201,2 = -115,49; реакция (5) - 376,7 - 241,84 + 115,9 = -502,64; реакция (6) - 393,51 - 241,84+ 115,9 + 1,5 0 = 519,45. Тогда уравнения реакций с термохимическим правилом знаков (тепловой эффект в кДж/моль) примут вид: СН3ОН + 0,5О2 = СН2О + Н2О + 156,54; (1) СН3ОН = СН2О + Н2 - 85,3; (2) СН3ОН = СО + 2Н2 - 126,35, (3) СН3ОН + Н2 = СН4 + Н2О + 115,49; (4) СН3ОН + О2 = НСООН + Н2О + 502,64; (5) СН3ОН + 1,5О2 = СО2 + 2Н2О - 519,45. (6) На основании материального баланса рассчитаем мольный расход метанола по каждой из реакций системы, а затем и количество выделяемого или поглощаемого тепла (см. табл. 9.2), откуда тепловой эффект процесса будет равен 604,8 кВт. Составим тепловой баланс процесса окисления метанола, предварительно рассчитав теплоемкости компонентов при заданной температуре 650 °С по уравнениям Ср =а + bТ + с'(1/T2); Ср=а + bТ + сТ2. Таблица 9.2. К расчету суммарного теплового эффекта процесса
Данные расчета занесены в табл. 9.3. Таблица 9.3. Средние теплоемкости компонентов реакции
Физическое тепло, вносимое компонентами в реактор, кВт: с метанолом 1860∙2,44∙t/3600 = 1,2607∙t; с кислородом 586∙1,05∙t/3600 = 0,1709∙t; с азотом 1920∙1,12∙t/3600 = 0,5973∙t. Всего на входе в реактор - 2,0289 Физическое тепло, уносимое компонентами из реакционной зоны, кВт: с формальдегидом 1220∙1,82∙800/3600 = 493,4; с метанолом 372∙2,44∙800/3600 = 201,7; с водяным паром 572∙2,13∙800/3600 = 207,7; с уксусной кислотой 126,5∙1,7∙800/3600 = 47,8; с диоксидом углерода 108∙1,13∙800/3600 = 27,1; с оксидом углерода 4,3∙1,13∙800/3600 = 1,1; с метаном 7,3∙4,05∙800/3600 = 6,6; с водородом 34,1∙14,5∙800/3600 = 109,9; с азотом 1920∙1,12∙800/3600 = 477,9; Всего на выходе - 1573,2. Примем потери тепла в количестве 5% от его расхода. Составим уравнение теплового баланса, из которого определим температуру на входе в реактор: 2,0289∙t + 604,8 = 1573,2 + 0,05∙1573,2. t= (1,05∙1573,2 - 604,8)/2,0289 = 516 °С. Занесем результаты расчета в табл. 9.4. Таблица 9.4. Тепловой баланс процесса получения формальдегида
Пример 9.3. Произвести тепловой расчет и составить тепловой баланс колонны синтеза аммиака в соответствии с исходными данными: температура в зоне реакции t = 500 °С; количество газовой смеси на входе в колонну V1 = 119025 нм3/ч; температура газовой смеси на входе t1 = 35 °С; количество газовой смеси на выходе из колонны V2 - 102329 нм3/ч; температура газовой смеси на выходе t2 - 110 °С. Состав газовой смеси, % (по объему): На входе На выходе Водород 74,1 62,06 Азот 24,7 20,7 Аммиак 1,2 17,24 Количество образующегося аммиака GNНз = 12500 кг/ч. Рабочее давление в аппарате Pр = 30 МПа. Температура воды: на входе 200 °С; на выходе 374 °С. Решение: Составим уравнение теплового баланса 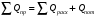 Приход тепла в колонну синтеза аммиака ( 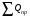 ). ).1) С газовой смесью Q1 = G1Cp1t1 где G1 - количество поступающей газовой смеси, кмоль/ч; Сρ1 - ее мольная теплоемкость, Сρ1 = 31,0 кДж/(кмоль∙К). Откуда Q1 = 30,0∙35∙119025/ 22,4 3600 = 1550 кВт. 2) Тепловой эффект реакции синтеза аммиака при высоком давлении. Определяется по уравнению qp = 38332 + (2,281∙10-5 + 3,519∙10-2/T + 19240/T3)∙30 000 000 + + 22,38∙T +1,057∙10-3∙T2 - 7,087∙10-6∙T3 где qр - тепловой эффект реакции, кДж/кмоль; Ризб - избыточное давление в реакторе, Па; Т - температура, К. В данном случае Т= 273 + 500 = 773 К; Р = 30∙106 Па. Откуда qp = 38332 + (2,281∙10-5 + 3,519∙10-2/773 + 19240/7733)∙30 000 000 + + 22,38∙773 +1,057∙10-3∙7732 - 7,087∙10-6∙7733 = 53000 кДж/кмоль. Общее количество тепла, выделяющееся при синтезе аммиака, будет равно Qp =qp∙GNH3/MNH3 = 53000∙12500/17,03∙3600 = 10 806 кВт 3) С охлаждающей водой на входе QB1 = i'W, где i' - энтальпия воды на входе при температуре 200 °С, равная 853 кДж/кг; W - расход охлаждающей воды, кг/с. QB1 = 853W Общий приход тепла в колонну синтеза аммиака 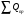 = 1550 + 10806 + 853W = 12356 + 853W, кВт. = 1550 + 10806 + 853W = 12356 + 853W, кВт.Расход тепла в колонне синтеза аммиака. 1) Расход тепла, уносимого с газовым потоком, равен Qp = G2Cp2t2 где G2 - количество уходящей газовой смеси, кмоль/ч; Ср2 - ее мольная теп лоемкость, Ср2 = 33,1 кДж/(кмоль∙К). Q2 = 33,1∙110∙(102329/(22,4∙3600) = 4620 кВт. 2) Тепло, уносимое охлаждающей водой, Qв2 =i"W, где i" - энтальпия воды на выходе при температуре 374 °С; i" = 2100 кДж/кг QB2 = 2100W. 3) Потери тепла в окружающую среду можно принять равными 5% от тепла, вносимого в колонну синтеза аммиака Qпот = 0,05(12356 + 853 W) кВт. Общий расход тепла Qрас = 4620 + 2100W + 0,05 (12356 + 853W) = 5247 + 2143W кВт. Уравнение теплового баланса 12356 + 853W = 5238 + 2143 W. Pасход охлаждающей воды будет равен W = 7118/1290 = 5,518 кг/с Составим таблицу теплового баланса (табл. 9.5). Таблица 9.5. Тепловой баланс колонны синтеза аммиака
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
