Проектирование хим. предприятий. Навчальний посібник до вивчення курсу основи проектування хімічних виробництв

• Название: Навчальний посібник до вивчення курсу основи проектування хімічних виробництв
• Анкор: Проектирование хим. предприятий.docx
• Дата: 22.12.2017
• Размер: 6.93 Mb.
• Имя файла: Проектирование хим. предприятий.docx
• Тип: Навчальний посібник; #12469
• страница: 18 из 27

Глава 10 ГИДРАВЛИЧЕСКИЕ РАСЧЕТЫ

10.1. РАСЧЕТ ДИАМЕТРА ТРУБОПРОВОДА

Внутренний диаметр трубопровода определяют из уравнения расхода (уравнения неразрывности):

Q = wS = (πd²w)/4; d = (4Q/πw)^0,5

G = ρwS = (πd²ρw)/4; d = (4G/πρw)^0,5

где d - внутренний диаметр трубопровода, м; w - скорость жидкости, м/с;

ρ - плотность жидкости, кг/м³; G - массовый расход жидкости, кг/с; Q - объемный расход жидкости, м³/с; S - площадь поперечного сечения потока, м².

Таким образом, при заданном расходе внутренний диаметр трубопровода обратно пропорционален квадратному корню из скорости жидкости.

Для протяженных трубопроводов такая зависимость требует технико-экономичес-

кого расчета, потому что с увеличением скорости жидкости уменьшается диаметр трубы, а с ним и капитальные затраты на изготовление и монтаж трубопровода. Однако при этом возрастают гидравлические сопротивления в трубопроводе и увеличиваются эксплуатационные затраты на перекачку жидкости. Оптимальный диаметр будет находиться в области равенства указанных затрат.

Для трубопроводов небольшой протяженности близкий к оптимальному диаметр можно определить по практически установленной скорости, представленной в табл. 10.1.

Таблица 10.1. Рекомендуемые оптимальные скорости

движения жидкости

Характер движения	Скорость жидкости, м/с
Жидкости, перемещаемые самотеком:
вязкие	0,1-0,5
маловязкие	0,5-1,0
Жидкости, перемещаемые насосом:	0,8-2,0
на всасывании
на нагнетании	1,5-3,0
Газы:	2,0-4,0
при естественной тяге
при небольшом давлении (0,1 МПа)	5,0-20,0
при повышенном давлении (>0,1 МПа)	15,0-25,0
Пары перегретые	30,0-50,0
Пары, насыщенные при абсолютном давлении, МПа:
более 0,1	15,0-25,0
0,05-0,1	20,0-40,0
0,02-0,05	40,0-60,0
0,005-0,02	60,0-75,0

После определения расчетного диаметра трубопровода необходимо выбрать его рабочий диаметр, исходя из материала трубы, способа ее изготовления и ряда стандартных диаметров для данного вида труб.

10.2. РАСЧЕТ ГИДРАВЛИЧЕСКИХ СОПРОТИВЛЕНИЙ

В ТРУБОПРОВОДЕ

Расчет гидравлических сопротивлений проводится для определения затрат энергии на перемещение жидкости с дальнейшим подбором насосов или комп-

рессоров. При движении жидкости по трубопроводу гидравлические сопротивления складываются из сопротивления трения и местных сопротивлений, возникающих за счет изменения скорости потока по величине и направлению.

Суммарные потери давления и напора определяются по уравнениям:



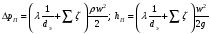
где ∆р_п - перепад давлений, Па; h_п - потери напора, м; d_э - эквивалентный диаметр, м; l - длина трубопровода, м; λ - коэффициент трения; g - ускорение силы тяжести, м/с²; ζ - коэффициент местных сопротивлений.

Эквивалентный диаметр для труб круглого сечения равен их диаметру, а для труб некруглого сечения определяется формулой

d_э = 4S/П

где П - смоченный периметр.

Коэффициент трения X в общем случае зависит от режима течения жидкости и шероховатости стенки трубы. При изотермическом ламинарном движении жидкости (Rе < 2300) коэффициент трения не зависит от шероховатости стенок трубы и определяется только числом Рейнольдса, которое рассчитывается по известной формуле

Rе = wd_эρ/μ

где μ - динамический коэффициент вязкости, Па∙с.

Коэффициент трения рассчитывается по уравнению

λ = А/Rе,

где А зависит от вида сечения канала и выбирается по табл. 10.2.

Таблица 10.2. Зависимость эквивалентного диаметра трубы от формы сечения

Форма сечения	dэ	А
Круг диаметром d	d	64
Квадрат со стороной а	а	57
Равносторонний треугольник со стороной а	0,58а	53
Кольцо шириной а	2а	96
Прямоугольник со сторонами а и b:
а/b0	2а	96
а/b =0,1	1,81a	85
а/b=0,25	1,6а	73
а/b= 0,5	1,3а	62
Эллипс (а - малая, b - большая полуоси):
а/b = 0,1	1,55а	78
а/b = 0,3	1,4а	73
а/b =0,5	1,3а	68

При изотермическом ламинарном течении жидкостей и газов по трубам потери давления на трение могут быть рассчитаны также по формуле Гагена – Пуазейля:

∆р_тр = 32wμρ/d²

При неизотермическом ламинарном течении жидкости, когда протекающая по трубе жидкость нагревается или охлаждается (температура стенки трубы отличается от температуры жидкости), коэффициент трения, полученный при изотермическом течении, умножается на поправочный коэффициент «х», который вычисляется по уравнению;



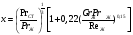
Здесь индексы «ж» и «ст» отвечают числам подобия, вычисленным по физическим свойствам жидкости при температурах жидкости и стенки.

Числа Прандтля и Грасгофа вычисляются по формулам:

,

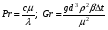где с - теплоемкость жидкости, Дж/(кг∙К); β - коэффициент ее объемного расшире-

ния, 1/К; ∆t - разность температур между стенкой и жидкостью, К.

При изотермическом турбулентном течении жидкости в гидравлически гладких трубах (стеклянных, медных, свинцовых)

λ = 0,3165/Re^0,25

Эта формула действительна при условии Rе < 100000.

Для гидравлически шероховатых труб коэффициент трения можно определить по графикам на рис. 10.1, где он зависит от числа Рейнольдса и шероховатости стенки трубы.



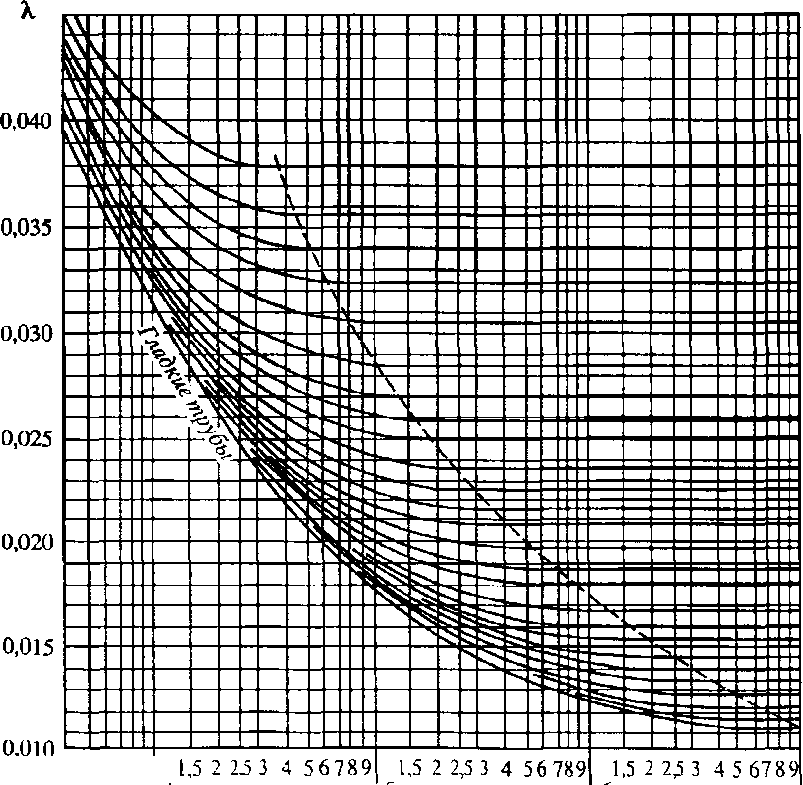
10⁴ 10⁵ 10⁶ 10⁷ Re

Рис. 10.1. Зависимость коэффициента трения от числа Рейнольдса и степени шероховатости трубы

Относительная шероховатость равна отношению абсолютной шероховатости «е» к эквивалентному диаметру трубы d_э. Ориентировочные средние значения абсолютной шероховатости можно определить по табл. 10.3.

Формула для расчета коэффициента трения в шероховатых трубах имеет вид



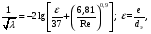
где е - абсолютная шероховатость трубопровода (см. табл. 10.3); ε - относительная шероховатость. При неизотермическом турбулентном течении жидкости коэффициент трения, рассчитанный для изотермического течения, умножается на поправочный множитель «х»:

x = (Pr_СТ/Pr_ж)^1/3

Таблица 10.3. Зависимость абсолютной шероховатости от типа трубы

Тип труб	Шероховатость «е», мм
Стальные, новые	0,06-0,1
Стальные, при незначительной коррозии	0,2
Стальные, старые, заржавленные	>0,67
Чугунные, новые	0,25-1,0
Чугунные, бывшие в эксплуатации	1,4
Алюминиевые	0,0015-0,06
Из латуни, меди, свинца, стеклянные	0,0015-0,01
Нефтепроводы, паропроводы	0,2
Воздуховоды сжатого воздуха	0,8

Для газов величина х ≈ 1, поэтому неизотермичность потока можно не учитывать.

Коэффициенты местных сопротивлений зависят от вида местного сопротивления и режима движения жидкости. Значения коэффициентов местных сопротивлений можно найти в справочной литературе.

10.3. ГИДРАВЛИЧЕСКОЕ СОПРОТИВЛЕНИЕ КОЖУХОТРУБЧАТЫХ ТЕПЛООБМЕННИКОВ

Для трубного пространства, а также для межтрубного пространства теплообменника без поперечных перегородок



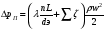
где L - длина одного хода; n - число ходов.

Для коэффициентов местных сопротивлений кожухотрубчатых теплообменников принимают следующие значения ζ:

Tрубное пространство:

вход и выход из теплообменника 1,5

поворот на 180° между ходами или секциями 2,5

вход в трубы и выход из них 1,0

Межтрубное пространство:

вход в межтрубное пространство и выход из него 1,5

поворот на 180° через перегородку 1,5

поворот на 90° в межтрубном пространстве 1,0

Если скорость жидкости в штуцерах больше, чем в теплообменнике, то расчет сопротивлений в штуцерах ведется по скорости жидкости в них.

При наличии поперечных перегородок в межтрубном пространстве гидравлические сопротивления в нем подсчитываются по нижеприведенным формулам при помощи числа Эйлера:

Eu = ∆p/ρw

Коридорные пучки:

Eu = b(34,5m) (S₁/d)^0,23 Rе^-0,26.

Шахматные пучки:

при S₁/d < S₂/d Eu = b(2 + 3,3m) Re^-0,28;

при S₁/d > S₂/d Еи = b(2,7 + 1,7m) Rе^-0,28,

где m - число рядов труб в пучке в направлении движения потока; d - наружный диаметр трубы; S₁и S₂ - поперечный и продольный шаги между трубами;

b - поправочный коэффициент, зависящий от угла атаки φ (угол между осью трубы и направлением движения потока):

φ, град	90	80	70	60	50	40	30	10
b	1	1	0,95	0,83	0,69	0,53	0,38	0,15

Скорость потока подсчитывается по самому узкому сечению пучка, значения физико-химических констант берутся при средней температуре жидкости. Число Рейнольдса рассчитывается по наружному диаметру трубы.

Пример 10.1. Жидкость, имеющая плотность ρ= 1200 кг/м³ и динамический коэффициент вязкости μ = 0,002 Па∙с, поступает самотеком из бака с постоянным уровнем в реактор (рис. 10.2).

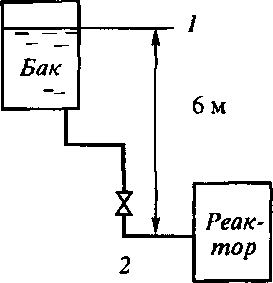Рис. 10.2. К примеру 10.1

Определить максимальный расход жидкости на входе в реактор. Уровень жидкости в баке находится на 6 м выше ввода жидкости в реактор. Трубопровод выполнен из алюминиевых труб с внутренним диаметром 50 мм. Общая длина трубопровода 16,4 м. На трубопроводе имеются три колена и кран.

В баке и реакторе давление — атмосферное.

Решение: Запишем уравнение Бернулли для сечений 1 и 2:



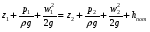
Так как z₁ - z₂ = Н; р₁ = р₂; и w₁ = 0,

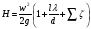
Напор H расходуется на все гидравлические сопротивления трубопровода. В последнем уравнении два неизвестных w и λ. Решение может быть найдено методом последовательных приближений.

Определим потери на местные сопротивления:

вход жидкости в трубопровод ζ= 0,5;

кран ζ= 2;

колено ζ = 1,1.

Таким образом Σζ = 0,5 + 2 + 3-1,1 = 5,8.

Исходное уравнение примет вид

6 = w²(1+ (16,4λ/0,05) + 5,8)

В случае движения без трения скорость жидкости

w = (6∙2∙9,81)^0,5 = 10,85 м/с.

Примем скорость в случае движения с трением в четыре раза меньше, т.е.

2,71 м/с. Определим при этой скорости коэффициент сопротивления

Rе=ρwd/μ= 2,71∙0, 05∙1200/0,002 = 81300

Отношение е/d для данного случая равно 0,0012, поэтому, используя уравнение, получим

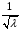= - 2lg[(0,0012/3,7) + (6,81/81300)^0,9]; λ = 0,0234

Определим скорость жидкости при найденном значении коэффициента трения

w = (118,92/(328λ + 6,8))^0,5 = 2,87 м/с.

Повторим вычисления

Rе = 2,87∙0,05∙1200/0,002 = 86100

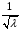= - 2lg[(0,0012/3,7) + (6,81/86100)^0,9]; λ = 0,0233

Совпадение достаточно хорошее, поэтому примем скорость жидкости равной

2,9 м/с. Тогда расход жидкости

V = wπd² = 2,9π0,05²/4 = 0,0057 м³/с = 20,6 м³ /ч.

10.4. ПОДБОР НАСОСОВ

Основными задачами при расчете насосов являются определение необходимого напора, создаваемого насосом, и мощности двигателя при заданном расходе жидкости. Насосы выбираются по каталогам или стандартам с учетом указанных параметров.

Напор определяется по формуле

Н = (р₁ – р₂)/ρg + h_г + h_п

где Н – напор насоса, м; р₁ - давление в аппарате на всасывании; р₂ - давление в аппарате на нагнетании; h_г - геометрическая высота подъема жидкости;

h_п - потери напора во всасывающей и нагнетательной линиях.

Полезная мощность, затрачиваемая на перемещение жидкости

N_п = (ρgHQ)/1000, кВт

Мощность на выходном валу

N = N_п/η_нη_п

где η_н - КПД насоса; η_п - КПД передачи от электродвигателя к насосу;

КПД насоса η_н = η₀η_гη_м

Здесь η₀ - объемный КПД, учитывающий перетекание жидкости из зоны большого давления в зону малого давления (для крупных центробежных насосов

0,96 - 0,98, для средних и малых насосов - 0,85 - 0,95); η_г - гидравлический КПД, учитывающий гидравлическое трение и вихреобразование (0,85-0,96); η_м - механический КПД, учитывающий механическое трение в подшипниках и уплотнениях (0,92 - 0,96).

КПД передачи зависит от наличия редуктора, при его отсутствии он равен 1, при наличии - 0,93 - 0,98. Зная Q, Н и N, можно по каталогам подобрать необходимый насос.

Мощность, потребляемая двигателем от сети N_дв больше номинальной вследствие потерь энергии в самом двигателе:

N_дв = N/η_дв

где η_дв - КПД электродвигателя, который ориентировочно принимается в зависимости от номинальной мощности N:

N,кВт	0,4 – 1,0	1,0 – 3,0	3,0 – 10	10 - 30	30 - 100	100 - 200
ηдв	0,7 – 0,78	0,78 – 0,83	0,83 – 0,87	0,87 – 0,9	0,9 – 0,92	0,92 – 0,94

Двигатель к насосу устанавливается несколько большей мощности, чем потребляемая, с запасом на возможные перегрузки:

N_уст = β N_дв

Коэффициент запаса берется в зависимости от величины N_дв:

Nдв ,кВт	<1,0	1,0 – 5,0	5,0 - 50	>50
β	2,0 – 1,5	1,5 – 1,2	1,2 – 1,15	1,1

Разрабатывая технологическую схему, необходимо учитывать, что высота всасывания насосов не может быть больше следующей величины:



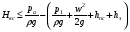
где р_а - атмосферное давление; р₁ - давление насыщенного пара перекачиваемой жидкости при рабочей температуре; w_вс - скорость жидкости во всасывающем трубопроводе; h_пс - потери напора во всасывающем трубопроводе; h_з -запас напо

ра для исключения кавитации.

Для центробежных насосов

h_з = 0,3(Qn²)^2/3,

где n - частота вращения вала, с^-1.

Для поршневых насосов

h_з =1,2(lf₁ω²r)/gf₂

где l - высота столба жидкости во всасывающем трубопроводе, отсчитываемая от поверхности жидкости в емкости; f₁,f₂ - площадь сечения поршня и трубопровода соответственно; ω - угловая скорость вращения кривошипа, рад/с; r - радиус кривошипа.

Пример 10.2. Подобрать центробежный насос для подачи 0,002 м³/с 10%-ного раст-

вора NaОН из емкости, находящейся под атмосферным давлением, в аппарат, рабо-

тающий под избыточным давлением 0,1 МПа. Температура раствора 40 °С; геомет-

рическая высота подъема раствора 15 м. Длина трубопровода на линии всасывания 3 м, на линии нагнетания 20 м. На линии всасывания установлен один вентиль, на линии нагнетания - один вентиль и дроссельная заслонка, имеются также два коле-

на под прямым углом.

Решение: Выбор диаметра трубопровода. Примем скорость раствора во всасыва-

ющем и нагнетательном трубопроводах одинаковой, равной 2 м/с. Тогда диаметр трубопровода



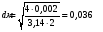
Принимаем трубопровод из стали Х18Н10Т диаметром 45 х 3,5 мм и уточняем ско-

рость раствора

w = (4∙0,002)/3,14∙0,038² = 1,76м/с

Определение коэффициента трения. Плотность 10%-ного раствора №ОН –

1100 кг/м³; его вязкость -1,16 10^-3 Па с. Тогда

Re = (1,76∙0,038∙1100)/0,00116 = 63420

Режим турбулентный. Примем абсолютную шероховатость труб 0,2 мм и тогда

ε = е/d = 0,2/38 = 0,0526.

Определим коэффициент трения



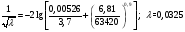
Определим сумму потерь на местные сопротивления.

На всасывающей линии:

вход в трубу ζ= 0,5;

вентиль (для d= 20 мм ζ = 8,0; для d = 40 мм ζ = 4,9);

интерполируя на диаметр 38 мм, получим ζ = 5,2;

Σζ_вс = 0,5+ 5,2 = 5,7.

На нагнетательной линии:

выход из трубы ζ = 1;

вентиль ζ = 5,2;

дроссельная заслонка ζ = 0,9;

колено под прямым углом ζ = 1,6;

Σζ_наг = 1+5,2+ 0,9 +2∙1,6= 10,3.

Определим потери напора.

Во всасываюшей линии

h_{п вс} = [(0,0325∙3)/0,038 + 5,7]1,76²/2∙9,81 = 1,3 м

В нагнетательной линии

h_{п наг} = [(0,0325∙20)/0,038 + 10,3]1,76²/2∙9,81 = 4,33 м.

Общие потери напора

h_п = 1,3 +4,33 = 5,63 м.

Подбор насоса. Определяем полный напор, развиваемый насосом

Н = 100000/(1100∙9,81) + 15 + 5,63 = 29,9 м.

Полезная мощность насоса

N_п = (0,002∙29,9∙9,81∙1100)/1000 = 645 Вт = 0,645 кВт.

Принимая η_п = 1 и η_н = 0,6, определим мощность на валу двигателя

N_дв = 0,645/(1∙0,6) = 1,075 кВт.

Мощность, потребляемая двигателем от сети при η_дв = 0,8

N = 1,075/0,8 = 1,34 кВт.

Принимая коэффициент запаса мощности β = 1,5, определяем установочную мощ-

ность электродвигателя

N_уст = 1,5∙1,34 = 2,01 кВт.

Подбираем центробежный насос марки Х8/30 с характеристиками:

производительность - 2,4∙10^-3 м³/с;

создаваемый напор - 30 м;

КПД насоса - 0,5.

Подбираем к насосу электродвигатель 4А100S2 номинальной мощностью 4 кВт, η_дв = 0.83, частота вращения вала 48,3 с^-1.

Рассчитаем предельную высоту всасывания. Определим запас напора, необходимый для исключения кавитации. Для центробежного насоса

h_з =0,3(0,002∙48,3²)^2/3 = 0,84 м.

Давление насыщенного пара при температуре 40 °С равно 7380 Па. Примем атмосферное давление равным 100 000 Па, а диаметр патрубка насоса равным диаметру трубопровода. Тогда

h_вс = 100000/(1100∙9,81) – (7380/1100∙9,81 + 1,76²/2∙9,81 + 1,3 + 0,84) = 6,3м.

Таким образом, центробежный насос можно расположить над уровнем раствора в емкости не выше чем на 6,3 м

Подбор машин для сжатия газов (компрессоров, газодувок, вентиляторов и т.д.) осуществляется аналогично подбору насосов по каталогам при заданном напоре и производительности.