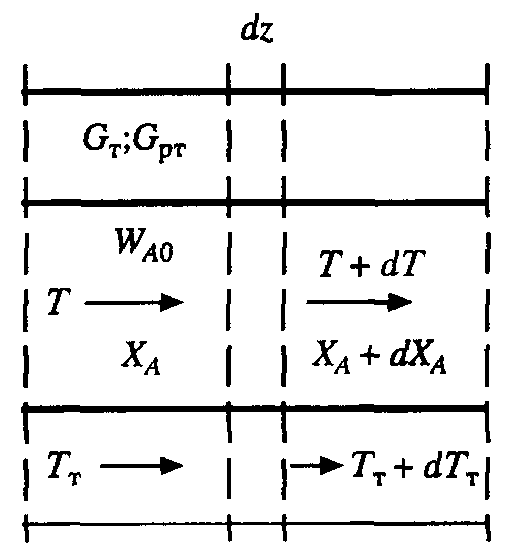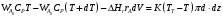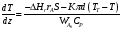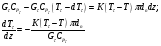Проектирование хим. предприятий. Навчальний посібник до вивчення курсу основи проектування хімічних виробництв
 Скачать 6.93 Mb. Скачать 6.93 Mb.
|
|
9.3. ТЕПЛООБМЕН В РЕАКТОРАХ При проведении реакции при постоянной температуре (изотермический про- цесс) степень превращения реагентов зависит от их концентрации и не зависит от температуры, поэтому уравнение материального баланса можно проинтегрировать и получить зависимость степени превращения от времени. При не изотермическом проведении процесса (адиабатическом или программно регулируемом) приходится решать совместно уравнения материального и теплово- го баланса с учетом зависимости скорости реакции от температуры и, при необхо- димости, процесса теплопередачи. Для создания приблизительно изотермических условий в реакторе можно применить несколько способов теплообмена: - теплообмен при постоянной скорости теплопередачи; когда реактор обогревается топочными газами или пламенем, коэффициент теплопередачи изменяется мало, а температура настолько высока, что изменение температуры реагентов практически не влияет на температурный напор; - теплообмен при постоянном коэффициенте теплопередачи; например, в аппаратах с мешалкой коэффициент теплопередачи зависит в основном от скорости перемешивания, которую можно держать постоянной, и скорость теплопередачи будет определяться изменением температуры реагентов; - автоматическое регулирование скорости теплопередачи путем регулирования расхода теплоносителя или изменения температуры его фазового перехода, напри- мер за счет давления. Последний способ, в принципе, является самым лучшим, но не всегда экономически целесообразным. Теплообмен в реакторах смешения. Рассмотрим химическую реакцию А + В = К + ∆Нr где ∆Нr - энтальпия реакции, Дж/моль. Запишем уравнение теплового баланса, относя мольные энтальпии к некоторой температуре Tс, например 0°, являющейся уровнем отсчета. Начальная температура реагентов T0, конечная - Т: 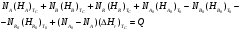 Q - количество отводимого или подводимого тепла, Дж. Если отсутствуют фазовые превращения, то энтальпии компонентов можно выразить через теплоемкости: 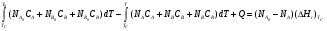 Если полагать, что теплоемкости не зависят от температуры в исследуемом интервале температур, а температура Т0 является уровнем отсчета, то уравнение упростится: (NАСА + NВСВ + NRСR) (Т - Т0) + (NА0 - NА)(∆Нr)То = Q Зная состав исходной смеси, можно связать степень превращения и температуру. Для стехиометрической смеси, разделив последнее уравнение на NA0 получим: [(1-ХA)(СA + СB) + ХAСR]∆Т = Q/NA0. После преобразований, получим: 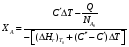 где С' и С" — сумма теплоемкостей реагентов и продуктов реакции соответствен но. Но, так как (∆Нr)Т0 + (С' - С")∆Т = (∆Нr)Т, то 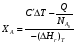 Здесь у энтальпии реакции и теплоты термодинамическое правило знаков, т.е. тепло, подводимое к системе, считается положительным. Для адиабатических условий Q=0, поэтому 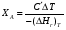 Пример 9.4. Для реакции первого порядка А + В = R, протекающей в адиабатических условиях, известны следующие данные: T0 = 28 °С; NA0 = NB0 = 1 кмоль; NR0 = 0; СА = СВ= 125 Дж/(моль ∙ К); СR = 167 Дж/(моль∙К); Н= - 11600 Дж/моль. Константа скорости реакции в узком интервале температур зависит линейно от температуры: k = 4,4 + 0,08(T-28) ч-1. Определить степень превращения реагентов и время ее достижения, если температура в реакторе повысилась за счет реакции на 28 К. Решение: Полагая отсутствие фазовых превращений в процессе, составим уравнение теплового баланса [(1 - XA)(125 + 125) + 167XA] (T-28) – 11600XA = 0; (250 – 83XA)(T - 28) = 11600XA; T - 28 = 28 = 11 600XA/(250 – 83XA); ХA = 0,503. Определим время реакции из баланса массы при условии реакции первого порядка τА = k(1-ХA). 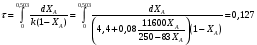 (Последний интеграл вычислен численным методом по формуле Симпсона.) Составим тепловой баланс в дифференциальной форме, полагая, что за элементар- ное время dτ скорость реакции rA и скорость теплопередачи R определяются урав- нениями 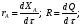 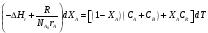 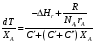 Теплоемкость и скорость реакции являются известными функциями температу- ры. Если скорость теплопередачи задана в функции от температуры, то послед- нее уравнение можно проинтегрировать. Для трех рассмотренных способов теп- лообмена связь между температурой и скоростью теплопередачи имеет вид: - теплообмен при постоянной скорости теплопередачи R = соnst; - теплообмен при постоянном коэффициенте теплопередачи R = КS (Tт - Т), КS = соnst, Тт = соnst; - автоматическое регулирование скорости теплопередачи R= ∆Нr∙rА = КS(Тт - Т), T= const. Здесь: К - коэффициент теплопередачи, Вт/(м2∙К); S - поверхность теплопереда- чи, м2; Тт - температура теплоносителя. Пример 9.5. Для реакции первого порядка известны следующие данные: энталь- пия реакции ∆Нr = 11600 Дж/моль; константа скорости реакции k= 0,8 ч-1; коэф- фициент теплопередачи К = 51 Вт/(м2∙К); начальная загрузка реагента NА0 = 2270 моль. Определить поверхность теплообмена, необходимую для поддержания постоянной температуры t = 49 °С до конечной степени превращения XA = 70%. Нагрев осуществляется паром, температуру которого Tт можно регулировать в пределах от 110 до 177 °С. Решение: Скорость подвода тепла должна быть наибольшей в начале процесса, когда ХА = 0, а скорость реакции — наибольшая. Расчет будем производить, используя уравнение ∆Нr∙rA=КS1(Тт-T) Откуда максимальная поверхность теплопередачи в этот момент выразится урав нением 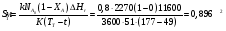 При такой поверхности и конечной степени превращения ХA = 0,7 температура теплоносителя должна быть равна 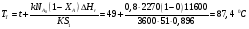 Эту температуру не обеспечить паром заданных параметров. Степень превраще- ния, отвечающая наиболее низкой заданной температуре теплоносителя110 °С, при поверхности теплопередачи S1 составит 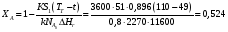 При температуре теплоносителя 110 °С и степени превращения 0,7 имеем 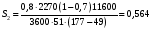 м2 м2При ХА = 0,524 и S2 = 0,564 м2 имеем 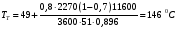 Таким образом, нагреватель должен состоять из двух параллельных змеевиков, один из которых с поверхностью S1 = 0,564 м2, а другой - S2 = 0,896 - 0,564 = 0,332 м2. При снижении температуры пара до 110 °С змеевик с поверхностью 0,332 м2 следует отключить. Кривые регулирования строятся по уравнениям 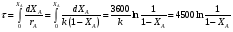 При XA ≤ 0,52 TТ = 49 + 128(1 - ХА); при ХА > 0,52 TT = 49 + 203(1-XA) Теплообмен в реакторах вытеснения. Если полагать отсутствие в реакци- онной зоне реактора идеального вытеснения радиальных градиентов температур, то можно составить три уравнения, одно из которых - баланс массы, второе - баланс тепла по реакционной массе и третье - баланс тепла по теплоносителю. Схема тепло - и массообмена в элементе реактора представлена на рис. 9.2. Уравнение баланса массы 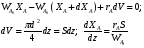
Совместное решение системы из трех дифференциальных уравнений дает возможность определить распределение степеней превращения, температур реакционной смеси и теплоносителя по длине реактора идеального вытеснения. Для адиабатического реактора идеального вытеснения получаем систему из двух дифференциальных уравнений 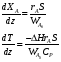 Пример 9.6. В гомогенном реакторе идеального вытеснения, представляющем собой трубу с внутренним диаметром 50 мм, протекает адиабатическая реакция второго порядка. Кинетические параметры реакции: энергия активации Е = 58200 Дж/моль, k0 = 2∙107 м3/(моль∙ч). Начальная концентрация реагента 20 кмоль/м3, его мольный расход 60 кмоль/ч, теплоемкость реакционной смеси 125 Дж/(моль∙К). Энтальпия реакции ∆Нr = - 10000 Дж/моль. Определить длину реактора при 90%-ной степени превращения, если начальная температура реагентов 770C Решение: Подставим исходные данные в систему дифференциальных уравнений материального и теплового баланса адиабатического реактора: 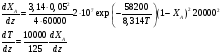 После преобразований получим: 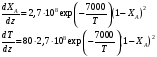 Решая полученную систему численным методом, можем найти длину реактора. Например, при решении модифицированным методом Эйлера при шаге интег- рирования 0,2 м получаем длину реактора 1,3 м (см. табл. 9.6). Таблица 9.6. Результаты решения дифференциального уравнения
9.4. РАСЧЕТ ЭНТАЛЬПИЙ И ТЕПЛОЕМКОСТЕЙ Как видно из приведенных уравнений, при тепловом расчете реактора необходимо обязательно знать энтальпии реакций, энтальпии фазовых переходов компонентов и теплоемкости компонентов. Если отсутствует табличное значение, то энтальпию реакции можно опре- делить по стандартным энтальпиям образования или сгорания компонентов в со ответствии с законом Гесса. Для реакции аА + bВ = rR + sS + ∆Нr, стандартная энтальпия реакции, рассчитанная по энтальпиям образования, равна ∆H°r = r H°R + s H°S - аН°А - b H°B. Соответственно по энтальпиям сгорания ∆H°r = а Н°А + b Н°В - r H°R - s H°S Значения стандартных энтальпий образования и сгорания можно найти в справочниках физико-химических величин. Значение энтальпии реакции при температуре реакции определяется уравнением ∆HTr = ∆H°r + (аСРА + bСРВ - rСРR - sСPS)(Т - Т0), где СРi - мольная теплоемкость i-того компонента; Т0 - «стандартная» температура; Т - расчетная температура. Энтальпии компонентов можно рассчитать, используя энтальпии фазовых пере ходов и температурные зависимости теплоемкостей фаз. При условии задания уровня отсчета Тс общая формула при этом будет иметь вид 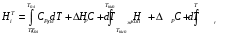 Индекс «пл» относится к температуре и энтальпии плавления, «кип» - к температуре и энтальпии кипения; «т», «ж» и «г» - соответственно к твердому телу, жидкости и газу. Температурные зависимости теплоемкостей для многих веществ можно найти в справочниках физико-химических величин, где они выражаются формулами: СР = а + bТ + сТ2 + ..., СР =а + bТ + с'Т-2. Если в данном температурном интервале в указанных уравнениях не окажется коэффициентов, то можно взять среднее значение теплоемкости, полученное из таблиц, или же рассчитанное по эмпирическим зависимостям. Эмпирические зависимости расчета теплоемкости зависят от фазового состояния вещества. Так мольную теплоемкость металлов и других кристаллических веществ можно ориентировочно рассчитать по правилу Дюлонга и Пти, которое предполагает, что каждый атом соединения вносит в молекулу долю теплоемкости, равную примерно 26 Дж/(моль∙К). Поэтому расчет удельной теплоемкости соединения можно провести по формуле 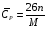 где n - число атомов в молекуле; М - молекулярная масса соединения, кг/моль. Теплоемкость многих твердых веществ - величина аддитивная и примерно равна сумме атомных теплоемкостей (правило Коппа): 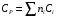 , ,где ni - число атомов данного вида; Сi - атомная теплоемкость, выбираемая из табл. 9.7. Таблица 9.7. Атомные составляющие теплоемкости твердых веществ
Вопрос о расчете теплоемкости некристаллических твердых соединений пока еще не решен, хотя с достаточно высокой ошибкой ее можно определить по правилу Коппа. Мольная теплоемкость идеальных газов при обычной температуре и давлении выражается соотношениями, приведенными в табл. 9.8. Таблица 9.8. Мольные теплоемкости идеальных газов
Здесь СV и СP - теплоемкости при постоянном объеме и постоянном давлении, соответственно, а R - универсальная газовая постоянная; R= 8,314 Дж/(моль∙К). Ориентировочное значение удельной теплоемкости в Дж/(кг∙К) можно получить из следующих формул: 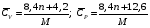 где n - число атомов в молекуле газа или пара; М - его молекулярная масса, кг/моль. Зависимость теплоемкости газов и парогазовых смесей от давления и температуры ориентировочно определяется по формуле 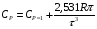 где СР - теплоемкость при атмосферном давлении, Дж/(моль∙К); π - приведенное избыточное давление газа, π = Р/Ркр; Р - избыточное давление газа, Па; Ркр - критическое давление газа, Па; τ - приведенная температура газа, τ = Т/Ткр; Т - температура газа, К; Ткр - критическая температура газа. Теплоемкость газовых и парогазовых смесей можно приближенно определить из выражения 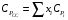 где хі - мольная или объемная доля компонента в смеси. Пример 9.7. Определить теплоемкость азота при температуре 50 °С и абсолют- ном давлении 20 МПа. Решение: По литературным данным для азота критическая температура равна 125,9 К, критическое давление - 3,285 МПа, молекулярная масса - 0,028 кг/моль. Определим изобарную теплоемкость при обычной температуре и атмосферном давлении СР=1 = 3,5∙8,314 = 29,1 Дж/(моль К). Приведенная температура τ = Т/Ткр = (273+50)/125,9 = 2,566 Приведенное избыточное давление π = Р/Ркр = (20-1)/3,285 Тогда СР = 29,1 + (2,531∙8,314∙5,783)/2,566 = 36,6 Или по удельной теплоемкости 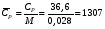 Удельная теплоемкость подавляющего большинства жидкостей лежит в пределах 1600 - 2400 Дж/(моль∙К), для большинства углеводородов этот параметр примерно равен 2100 Дж/(моль∙К). Ориентировочную оценку мольной теплоемкости жидкостей можно провести, используя правило Коппа, которое применимо для температуры 20 °С: 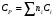 где ni - число атомов данного вида; Сi - атомная теплоемкость, выбираемая из табл. 9.9. Мольную теплоемкость жидкостей при 20 °С можно вычислить по методу Джонсона - Хуанга: 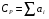 , ,где аi - атомная или групповая составляющие (см. табл. 9.10). Таблица 9.9. Атомные составляющие теплоемкости жидкостей
Таблица 9.10. Атомные и групповые составляющие метода Джонсона - Хуан га
Пример 9.8 Вычислить по методу Джонсона - Хуанга теплоемкость бензола (С6Н6) при 20 °С. Решение: Бензол можно представить состоящим из шести групп =СН—, тогда Ср=6∙22,6 = 135,6 Дж/(моль∙К). Опытное табличное значение 136,2 Дж/(моль∙К). Вторая формула Джонсона - Хуанга дает возможность получить температурную зависимость теплоемкости СР = а + bТ + сТ2 + dТ3 Коэффициенты а, b, с и d представлены в табл. 9.11. Важной характеристикой при тепловом расчете реакторов может являться энтальпия испарения. В том случае, если нельзя найти ее табличное значение, ее можно рассчитать. Наиболее простым, но и не вполне точным методом является правило Трутона: Lисп.к = 87,9 Тк, где Lисп.к - энтальпия испарения при температуре кипения, Дж/моль; Тк - температура кипения, К. Более точным является метод Джиаколоне: 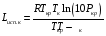 где Ткр и Ркр - критические температура (К) и давление (МПа). Таблица 9.11. Расчет теплоемкости по методу Джонсона—Хуанга 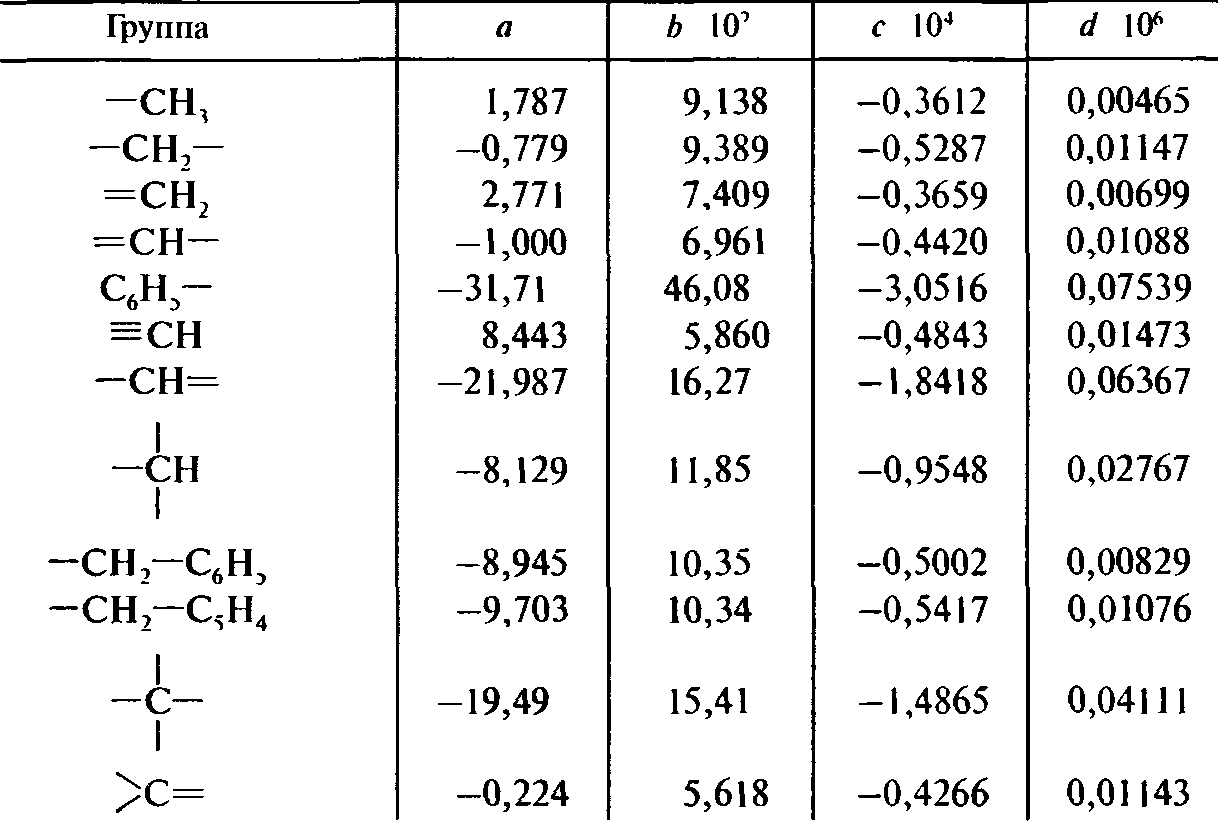 Энтальпию плавления можно приближенно определить по формуле Lпл = 56,5Тпл где Lпл - энтальпия плавления, Дж/моль; Тпл - температура плавления, К. Для органических соединений соотношение между энтальпиями испарения и плавления имеет вид Lпл≈ 0,356 Lисп.к. |