Приложение 1_Эконометрика. Оценочные материалы текущего контроля успеваемости. Методические материалы по проведению процедур оценивания

• Название: Оценочные материалы текущего контроля успеваемости. Методические материалы по проведению процедур оценивания
• Дата: 29.03.2023
• Размер: 4.57 Mb.
• Имя файла: Приложение 1_Эконометрика.doc
• Тип: Документы; #1024553
• страница: 35 из 42

Значения параметров регрессии 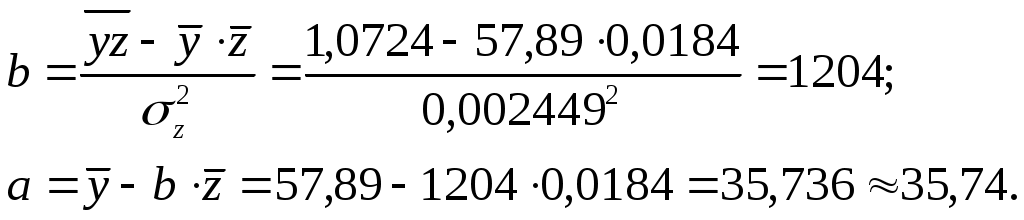и составляют:



Тогда .

Индекс корреляции: .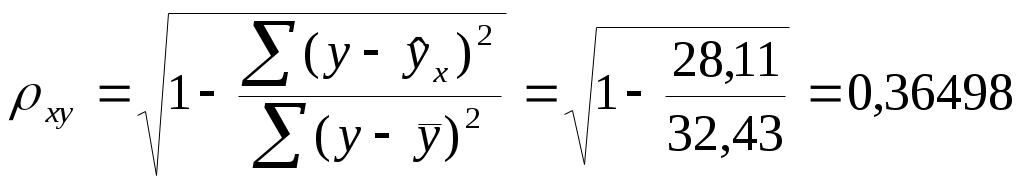

Следовательно, связь умеренная.

1. 
   Ошибка аппроксимации для всех функций повышенная:
   

а) ,

б) ,

в) ,

г) ; но в допустимых пределах.

F-критерий Фишера: а)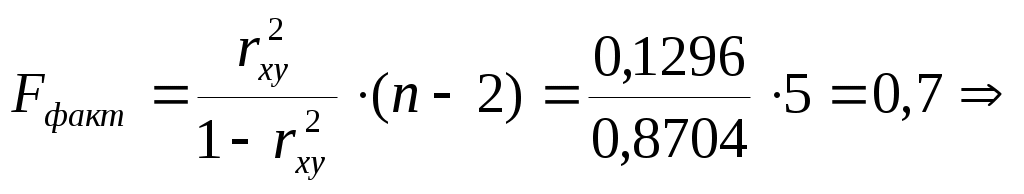

поскольку , с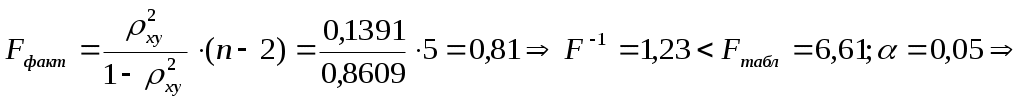ледует рассмотреть ; . Что говорит о принятии гипотезы о статистической не значимости параметров уравнения и показателя тесноты связи и случайной природе выявленной зависимости.

б)

гипотеза п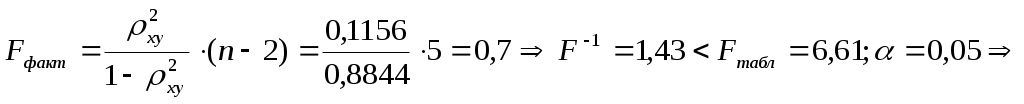ринимается.

в)

гипотеза п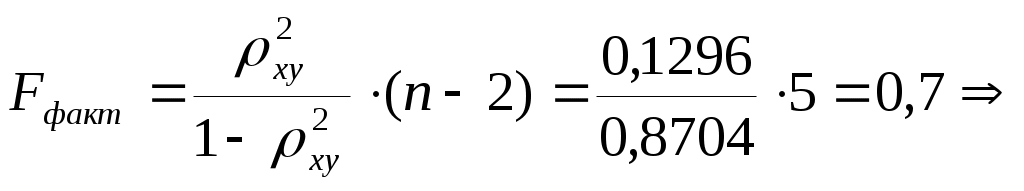ринимается.

г) гипотеза принимается, т.к. .

Пример 2. По 12 территориям региона вводятся данные (таблица 6).
Таблица 6

Номер региона	х	у
1	78	133
2	82	148
3	87	134
4	79	154
5	89	162
6	106	195
7	67	139
8	88	158
9	73	152
10	87	162
11	76	159
12	115	173

Требования:

1. 
   Постройте линейное уравнение парной регрессии у от х.
   
2. 
   Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.
   
3. 
   Оценить статистическую значимость параметров регрессии и корреляции.
   
4. 
   Выполнить прогноз у при прогнозном значение х, составляющем 107% от среднего уровня.
   
5. 
   Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
   

Решение:

1. 
   Для расчета параметров уравнения линейной регрессии строим расчетную таблицу 7.
   

Таблица 7

№ региона
1	78	133	10374	6084	17689	149	-16	12	256
2	82	148	12136	6724	21904	152,6	-4,6	3,1	21,16
3	87	134	11658	7569	17956	157	-23	17,2	529
4	79	154	12166	6241	23716	149,9	4,1	2,7	16,81
5	89	162	14418	7921	26244	158,8	3,2	1,98	10,24
6	106	195	20670	11236	38025	173,9	21,1	10,8	445,21
7	67	139	9313	4489	19321	139,2	-0,2	0,0	0,04
8	88	158	13904	7744	24964	157,9	0,1	0,0	0,01
9	73	152	11096	5329	23104	144,6	7,4	4,9	54,76
10	87	162	14094	7569	26244	157	5	3,1	25
11	76	159	12084	5776	25281	147,2	11,8	7,4	139,24
12	115	173	19895	13225	29929	181,95	-8,95	5,2	80,1025
Итого	1027	1869	161808	89907	294377	1869,05	-0,05	68,38	1577,6
Среднее значение	85,6	155,8	13484,0	7492,3	24531,4	Х	Х	5,7	Х
	164,94	257,76
	12,84	16,05

Тогда параметры регрессии: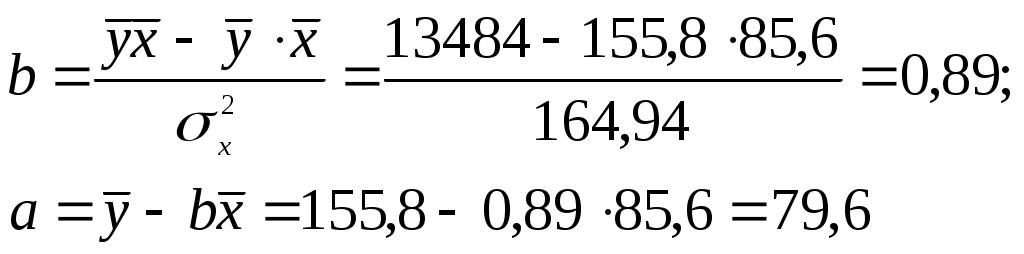



Уравнение регрессии: , т.е. с увеличением х на 1ед. у возрастает в среднем на 0,89ед.

2. 
   Тесноту линейной связи оценит коэффициент корреляции: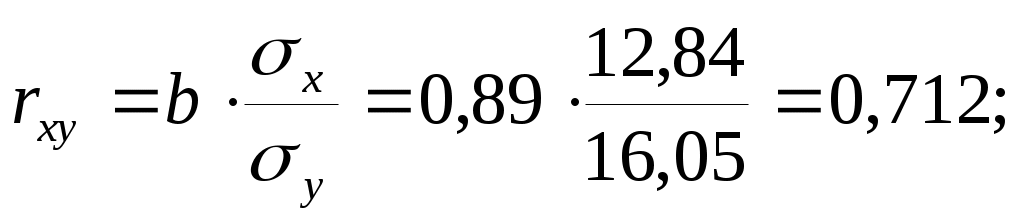
   

Это означает, что 51% вариации у объясняется вариацией фактора х.

Качество модели определяет средняя ошибка аппроксимации:

.

Качество построенной модели оценивается как хорошее, т.к. не превышает 8-10%.

3. 
   Оценку статистической значимости параметров регрессии проведем с помощью -статистики Стьюдента и путем расчета доверительного интервала каждого из показателей. Выдвигаем гипотезу о статистически не значимом отличии показателей от нуля: . для числа степеней свободы и составит 2,23.
   

Определим случайные ошибки :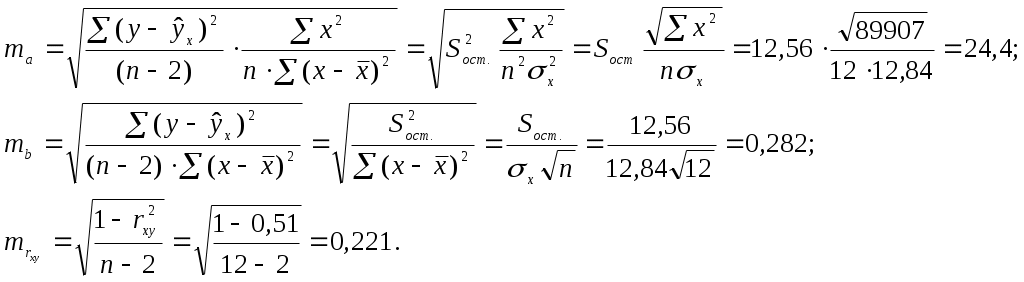



Тогда 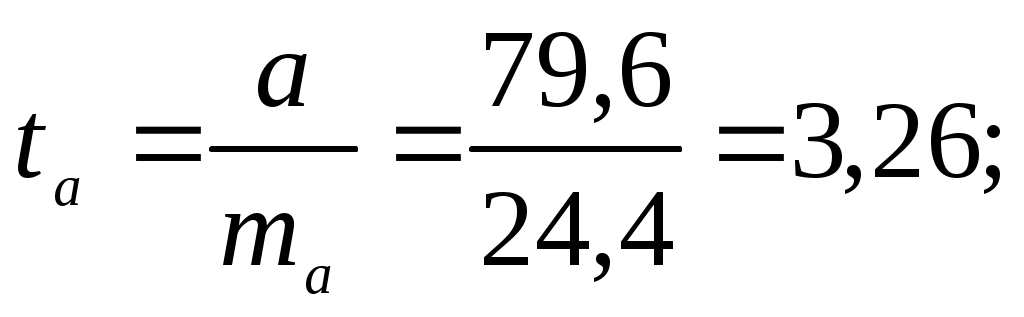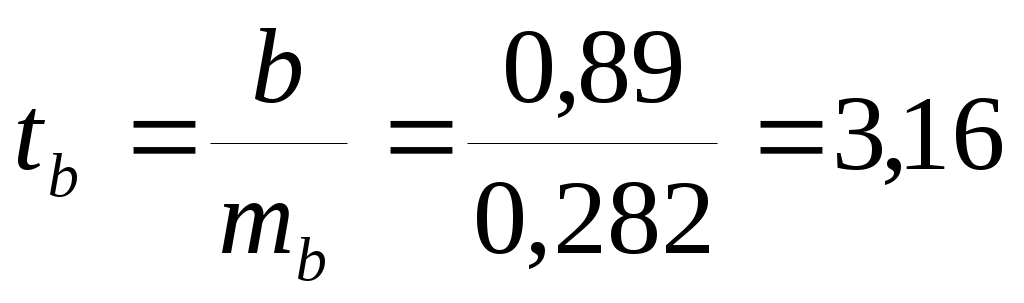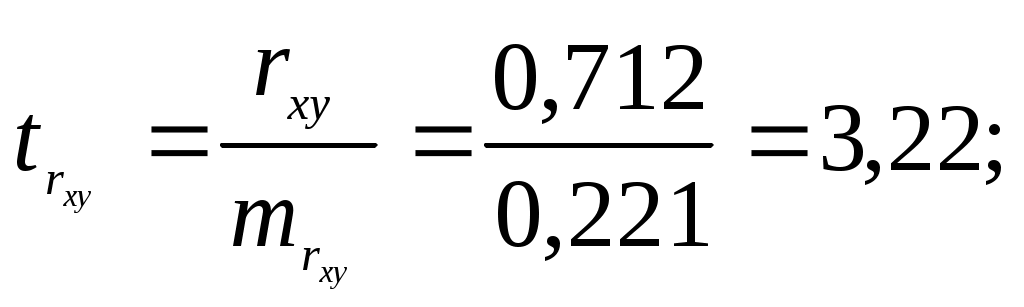-статистики Стьюдента:

;

Фактические значения 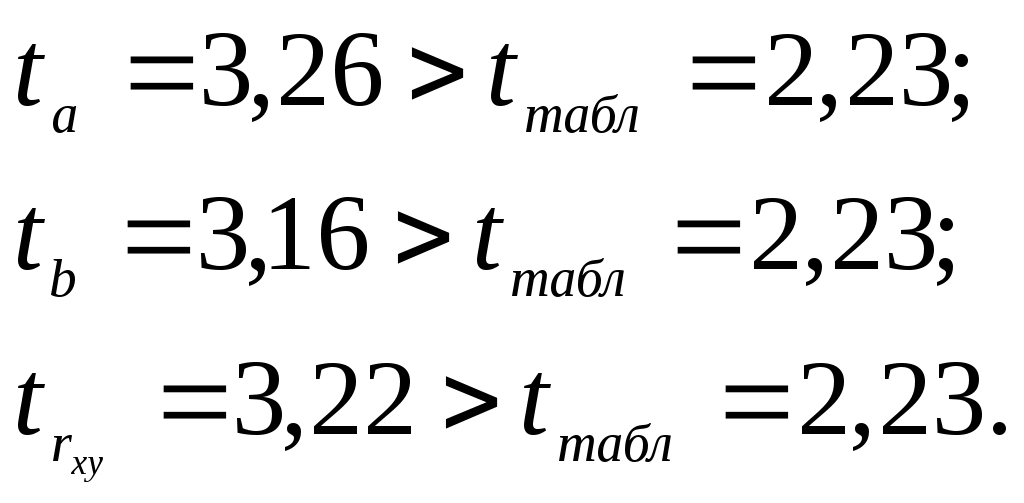-статистики превосходят табличные значения:



Поэтому гипотеза отклоняется, т.е. и не случайно отличаются от нуля, а статистически значимы.

Рассчитаем доверительный интервал для 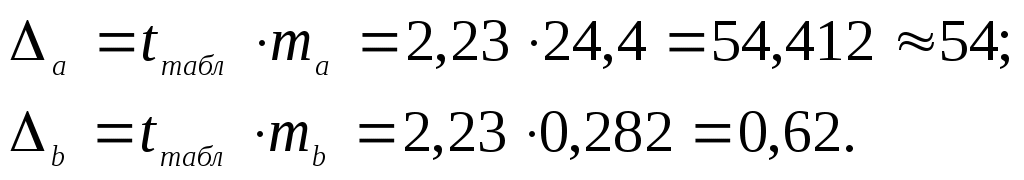и . Для этого определим предельную ошибку для каждого показателя:



Доверительные интервалы:







Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью параметры и , находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.

4. 
   Полученные оценки уравнения регрессии позволяют использовать для прогноза. Если прогнозное значение х составит:
   

ед.; тогда прогнозное значение у составит:

ед.

5. 
   Ошибка прогноза составит: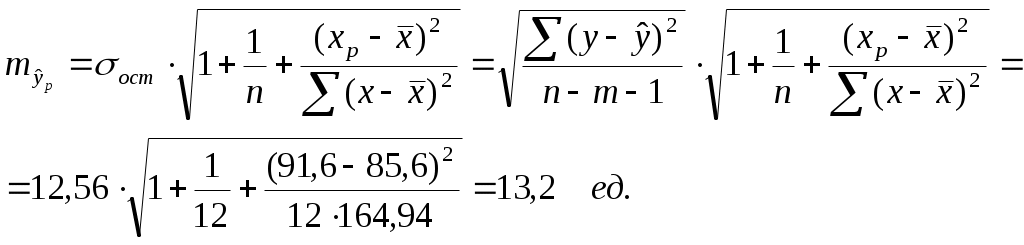
   

Предельная ошибка прогноза, которая в 95% случаев не будет превышена, составит: .

Доверительный интервал прогноза:







Выполненный прогноз у оказался надежным ( 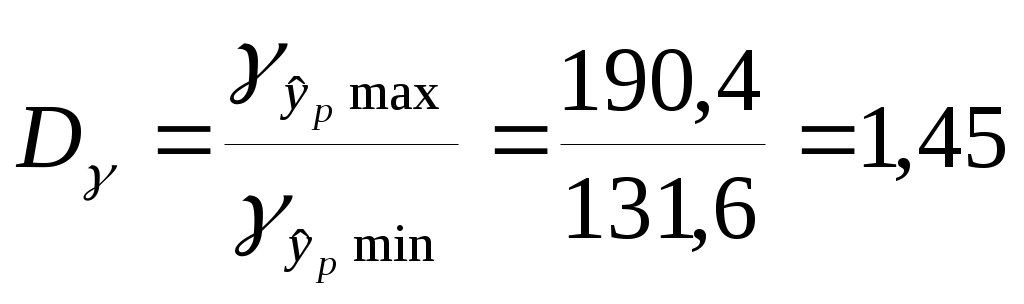), но не точным, т.к. диапазон верхней и нижней границ доверительного интервала составляет 1,45 раза:

.
Пример 3. По 30 территориям России имеются данные, представленные в таблице 8:

Таблица 8

Признак	Среднее значение	Среднее квадратическое отклонение	Линейный коэффициент парной корреляции
Среднедневной душевой доход, руб., у	86,8	11,44	-
Среднедневная заработная плата 1го работающего, руб., х1	54,9	5,86
Средний возраст безработного, лет, х2	33,5	0,58

Требуется:

1. 
   Построить уравнение множественной регрессии в стандартной и естественной форме; рассчитать частные коэффициенты эластичности, сравнить их с и , пояснить различия между ними.
   
2. 
   Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции, сравнить их с линейными коэффициентами парной корреляции, пояснить различия между ними.
   
3. 
   Рассчитать общий и частные - критерии Фишера.
   

Решение:

1. 
   Линейное уравнение множественной регрессии у от х₁ и х₂ имеет вид:.
   

Для расчета его параметров применим метод стандартизации переменных и построим искомое уравнение в стандартизированном масштабе:

Расчет 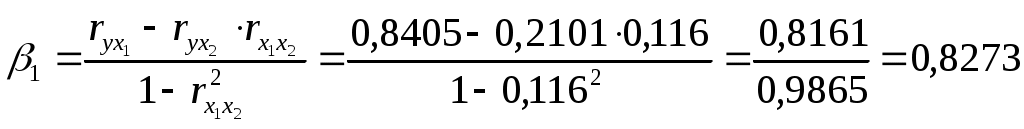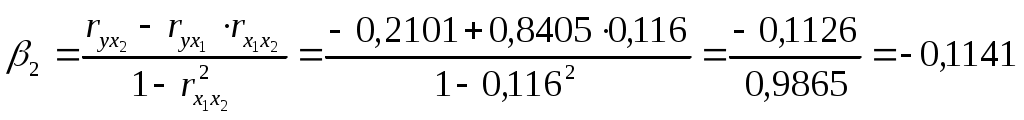-коэффициентов выполним по формулам:

;

;

Получим уравнение: .

Для построения уравнения в естественной форме рассчитаем 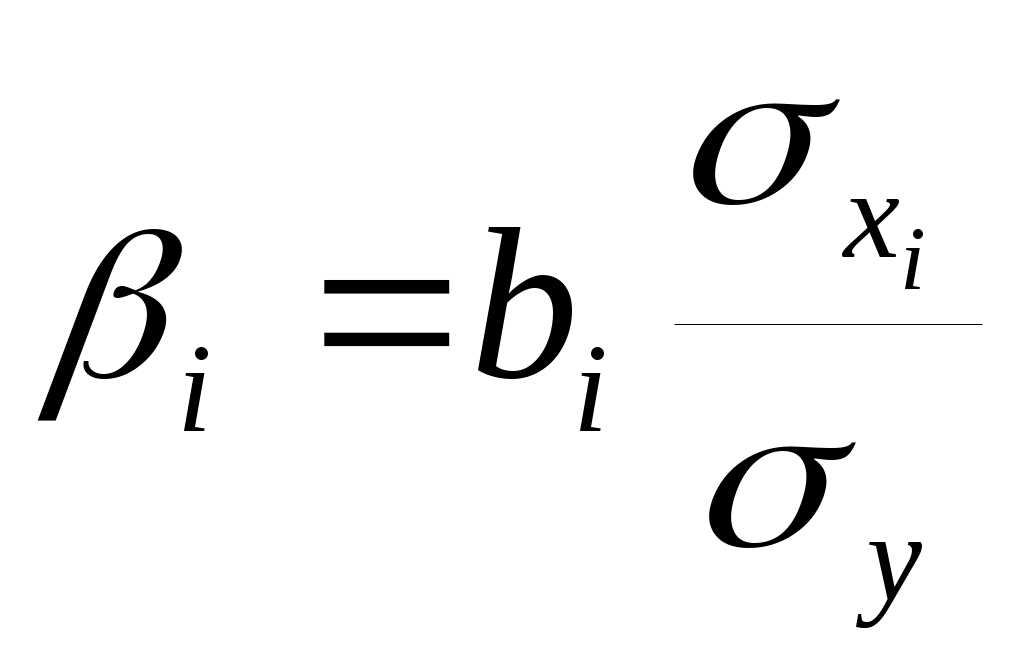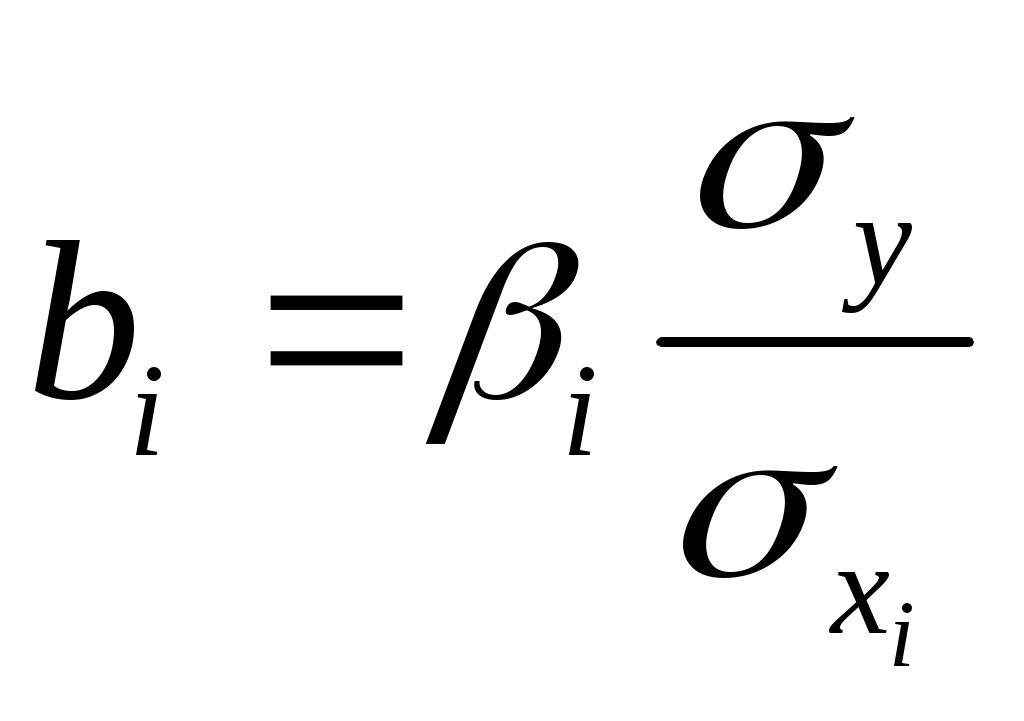и , используя формулы для перехода от к :

; ; .

Значение а определим из соотношения:

.



Для характеристики относительной силы влияния х₁ и х₂ на у рассчитаем средние коэффициенты эластичности: ;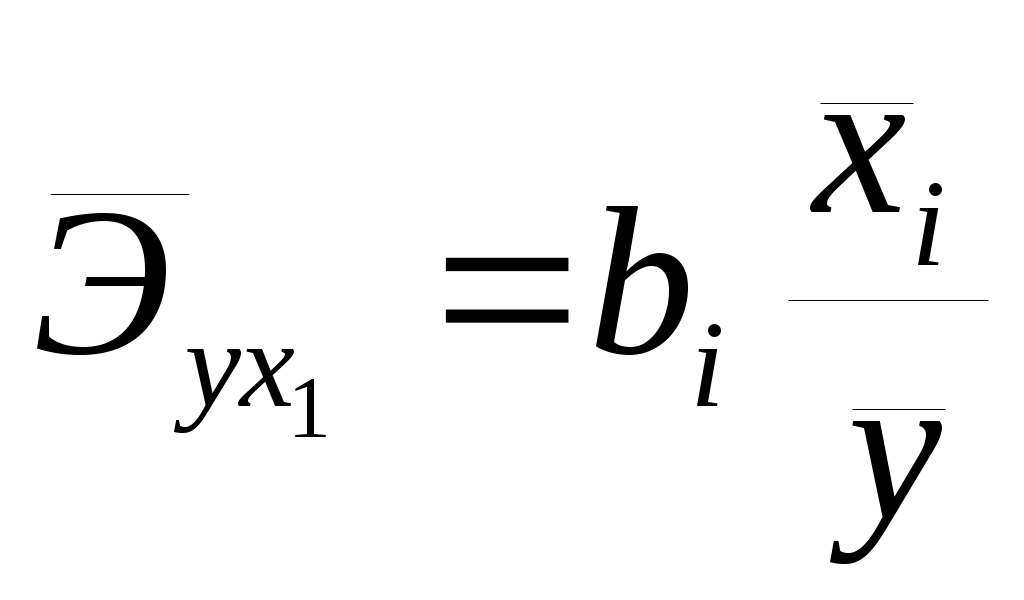

; .

С увеличением средней заработной платы х₁ на 1% от ее среднего уровня средний душевой доход у возрастает на 1,02% от своего среднего уровня; при повышении среднего возраста безработного х₂ на 1% среднедушевой доход у снижается на 0,87% от своего среднего уровня. Очевидно, что сила влияния, средней заработной платы х₁ на средний душевой доход у оказалась большей, чем сила влияния среднего возраста безработного х₂. К аналогичным выводам о силе связи приходим при сравнении модулей значений и :

.

Различия в силе влияния фактора на результат, полученные при сравнении и , объясняются тем, что коэффициент эластичности исходит из соотношения средних: ; а коэффициент - из соотношения средних квадратических отклонений: .

2. Линейные коэффициенты частной корреляции здесь рассчитываются по рекуррентной формуле: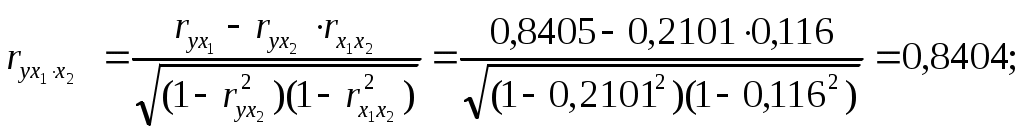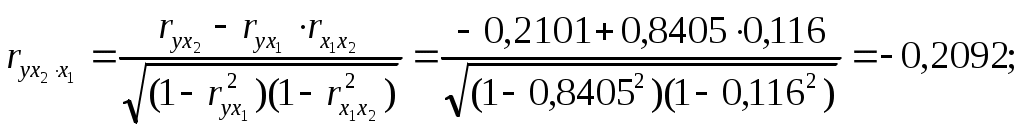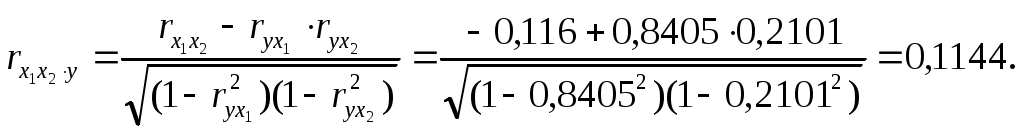







Если сравнить значения парной и частной корреляции, то приходим к выводу, что из-за слабой межфакторной связи ( ) коэффициенты парной и частной корреляции отличаются незначительно: выводы о тесноте и направлении связи на основе коэффициентов парной и частной корреляции совпадают:

; ; ;

; ; .

Расчет линейного коэффициента множественной корреляции выполним с использованием коэффициентов и :

.

Зависимость у от х₁ и х₂ характеризуются как тесная, в которой 72% вариации среднего душевного дохода определяется вариацией учтенных в модели факторов: средней заработной платы и среднего возраста безработного. Прочие факторы, не включенные в модель, составляют соответственно 28% от общей вариации у.

3. Общий F-критерий проверяет гипотезу Н₀ о статистической значимости уравнения регрессии и показателя тесноты связи (R²=0):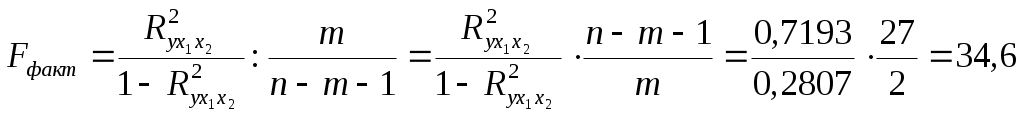

;

F_табл=3,4; при .

Сравнивая F_табл и F_факт, приходим к выводу о необходимости отклонить гипотезу Н₀, т.к. F_табл=3,4<F_фактл=34,6. С вероятностью 1- делаем заключение о статистической значимости уравнения в целом и показателя тесноты связи , которые сформировались под неслучайным воздействием факторов х₁ и х₂.

Частные F-критерии - 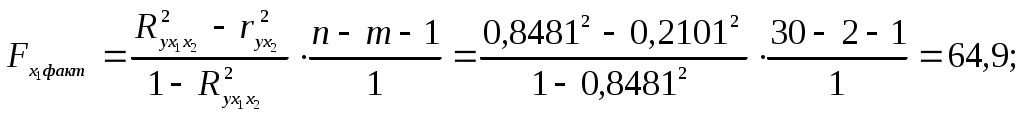и оценивают статистическую значимость присутствия факторов х₁ и х₂ в уравнении множественной регрессии, оценивают целесообразность включения в уравнение одного фактора после другого фактора, т.е. оценивает целесообразность включения в уравнение фактора х₁ после того, как в него был включен фактор х₂. Соответственно указывает на целесообразность включения в модель фактора х₂ после фактора х₁:



; при .

Сравним F_табл и F_факт приходим к выводу о целесообразности включения в модель фактора х₁ после фактора х₂, т.к. гипотезу Н₀ о не существенности прироста за счет включения дополнительного фактора х₁ отклоняем и приходим к выводу о статистически подтвержденной целесообразности включения фактора х₁ после фактора х₂.

Целесообразность включения в модель фактора х₂ после фактора х₁ проверяет :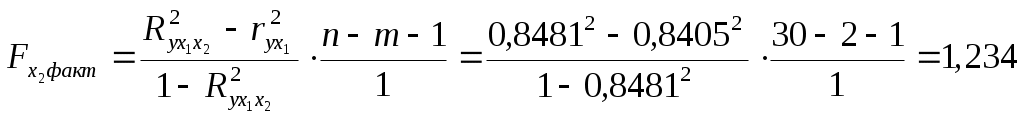



Низкое значение (немногим >1) свидетельствует о статистической не значимости прироста за счет включения в модель фактора х₂ после фактора х₁.

Таким образом подтверждается нулевая гипотеза Н₀ о нецелесообразности включения в модель фактора х₂ (средний возраст безработного). Это означает, что парная регрессионная модель зависимости среднего дохода от средней заработной платы является достаточно статистически значимой, надежной и что нет необходимости улучшать ее, включая дополнительный фактор х₂ (средний возрасте безработного).
Пример 4. Имеются данные (таблица 9) за 5лет:

Таблица 9

год	У1	У2	Х1	Х2
1	60	5,0	1300	60
2	62	4,0	1300	56
3	65	4,2	1500	56
4	62	5,0	1600	63
5	66	3,8	1800	50