Статистика. стат практ с отв к. Описательная статистика 3 Виды средних величин 3
 Скачать 121.82 Kb. Скачать 121.82 Kb.
|
|
| 50-100 | 176 | 50 | 176/50 = 3,52 |
В данном случае интервалы разной величины. И выбрать интервал с
наибольшей частотой в качестве модального мы не можем. Так как важна
частота на единицу длины интервала.
Например, второй интервал ширины h — 5 содержит 45 значений
признака, а третий, в два раза большей ширины /г = 10, содержит в два раза
больше единиц признака - 90. Т.о. частота на единицу длины интервала у
них одинаковая (45 / 5 = 90/10 = 9) несмотря на то, что количество значений
признака во втором интервале меньше, чем в третьем. Потому нельзя сказать,
что вероятность встретить повторяющиеся значения признака в третьем
интервале больше, чем во втором.
В данном случае, когда расчет модального значения выполняется по
рядам распределения с неравными интервалами, необходимо вычислить
плотности и уже по ним, найдя максимальное значение плотности,
определить модальный интервал. А затем, используя формулу (1.2),
определить моду.
В нашем случае наибольшая плотность / '^тах = 12,5. Соответственно,
модальным является интервал (20-50). Подставив соответствующие значения
в форуму (1.2) получаем:
/мо — fl4o-1
Мо = хМп + h
СfMo fMo-О + С/мо fMo +1)
12,5-9
= 20 + 30 ■ ———т—————— = 28,4 тыс. чел10.
(12,5-9)+ (12,5-3,52)
Таким образом, в стране А чаще всего встречаются города и поселки городского типа с численностью населения 28,4 тыс. чел.
10 Проверка. Мо = 28,4 тыс. чел. принадлежит модальному интервалу (20-50), значит мы верно вычислили показатель Мо.
28
| Число поездок в день | Количество граждан, совершающих в день данное количество поездок |
| 0 | 221 |
| 1 | 146 |
| 2 | 434 |
| 3 | 405 |
| 4 | 302 |
| 5 | 112 |
Анализ формы распределения.
Степень асимметричности распределения характеризуется коэффициентом асимметрии (As):
'LidXi-x)3
ll3
As = — = (для несгруппированных)
a a
или
T.jjXj - x)3 ■ fj
As = ^ = (для сгруппированных данных),
с
а также коэффициентом асимметрии Пирсона (Ауп):
х — Мо As„=—^—, где а- среднее квадратическое отклонение; fa — третий центральный момент;
Xi - значение признака (для интервального ряда хг заменяют х!t - центральным значением интервала);
х - среднее значение признака; п — количество наблюдений в распределении;
29
f - частоты распределения; Mo - мода.
Знак коэффициента асимметрии и коэффициента асимметрии Пирсона совпадает.
Для симметричных распределений (вкл. нормальное распределение) варианты (хг), равноудаленные от х, имеют одинаковую частоту, потому //3 и соответственно As — 0.
Если As > 0, то в вариационном ряду преобладают варианты, которые больше средней (х) и распределение имеет более длинную ветвь справа (скошено вправо). Такое распределение называют правосторонне ассиметричным, в этом случае х > Мо.
Примером такого распределения может служить средний уровень заработной платы (з/п) в стране. Когда большинство людей получают зарплату меньше среднего значения (Мо < х), но незначительная группа людей получает з/п много выше среднего уровня (скошено вправо), что и выводит среднюю заработную плату на уровень выше Мо.
Если As < 0, то в вариационном ряду преобладают варианты, которые меньше средней (х) и распределение имеет более длинную ветвь слева (скошено влево). Такое распределение называют левосторонне ассиметричным, в этом случае Мо > х.
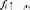
\

Рис. 1. Правосторонняя асимметрия (As > 0)
30

х Мо xi
Рис. 2. Левосторонняя асимметрия (As < 0)
Примером такого распределения может служить средний по стране уровень оплаты за коммунальные услуги. Когда большинство людей платят больше среднего значения (Мо > х), но за счет того, что незначительная группа людей платит значительно меньше среднего уровня (скошено влево), средний уровень расходов на ЖКХ смещается в меньшую сторону, становиться меньше Мо.
Для распределений по форме близких к нормальному закону, медиана находится между модой и средней величиной. Для таких распределений при правосторонней асимметрии х > Me > Мо, при левосторонней асимметрии х < Me < Мо.
Для оценки крутизны (заостренности) распределения вычисляют эксцесс (Ех):
LOi *)4
Ех = ^ — 3 = ^ 3 (для несгруппированных)
или
YiiXj - х)4 ■ fj
Ex = — 3 = 3 (для сгруппированных данных),
сг4
где а- среднее квадратическое отклонение;
//4 - четвертый центральный момент;
Xf - значение признака (для интервального ряда хг заменяют х'г центральным значением интервала);
31
| Заработная плата, тыс. руб. | Количество рабочих, чел. |
| 20,260-21,510 | 6 |
| 21,510-22,760 | 12 |
| 22,760-24,010 | 29 |
| 24,010-25,260 | 24 |
| 25,260-26,510 | 6 |
| 26,510-27,760 | 5 |
| 27,760-29,010 | 4 |
Решение. Так как распределение задано интервальным рядом (равные интервалы с шагом h = 1 250 руб.) показатели асимметрии и крутизны определим по формулам:
ZiiXj - х)3 ■ fj
As = (для сгруппированных данных),
о о
'Ziixj - х)А ■ fj
Ex = — 3 = 3 (для сгруппированных данных).
