Организация медикосоциального исследования. Статистические таблицы

• Название: Организация медикосоциального исследования. Статистические таблицы
• Дата: 19.06.2022
• Размер: 1.91 Mb.
• Имя файла: Teoria_OZZ.docx
• Тип: Занятие; #603480
• страница: 3 из 29

Тема: «Характеристика и анализ статистических данных. Средние величины и показатели вариации»

Средняя величина - это величина, одним числом характеризующая всю совокупность в целом. Различают несколько видов средних величин: В практической деятельности врача наиболее часто используются средняя арифметическая (М) и особые средние - мода (Мо) и медиана (Ме).

Для расчета средних величин необходимо соблюдать следующие условия:

- средние величины должны быть рассчитаны на основе качественно однородных статистических групп;

- средние величины исчисляются на совокупностях, имеющих достаточно большое число наблюдений.

В медико-социальных исследованиях используются следующие виды средних величин:

- средняя арифметическая;

- средняя арифметическая взвешенная;

- средняя гармоническая взвешенная;

- средняя геометрическая невзвешенная;

- средняя геометрическая взвешенная;

- средняя квадратическая невзвешенная;

- средняя квадратическая взвешенная.

К средним величинам относят также моду как наиболее типичное значение и медиану как середину распределения случайной величины.

При изучении общественного здоровья, анализе деятельности учреждений здравоохранения, оценке работы медицинского персонала из всех видов средних величин наиболее часто используется средняя арифметическая, которая может быть простой и взвешенной.

Ряд наблюдений, все элементы которого упорядочены по возрастанию, называется вариационным рядом. Элемент вариационного ряда - варианта.

Средняя арифметическая простая - средняя вариационного ряда х₁, х₂,..., х_n, где каждая варианта записана столько раз, сколько встречается. Вычисляется по формуле: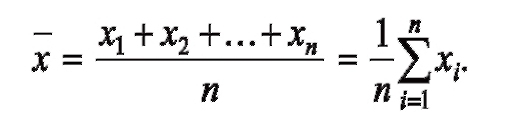



Среднюю арифметическую значений х₁, х₂, х? можно записать иначе, с учетом частоты повторений каждого из значений. Получаем среднюю арифметическую взвешенную вариационного ряда, где k различных значений k   n.

Тогда средняя арифметическая взвешенная записывается как: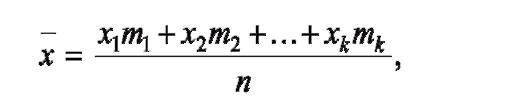



где каждое число m_i - частота соответствующего значения x_i, причем: m₁ + m₂ +...+ m_k= n.

Формулу расчета средней арифметической взвешенной можно представить в следующем виде: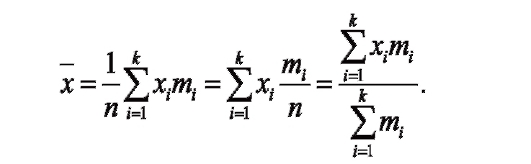



Средняя арифметическая простая и средняя арифметическая взвешенная - это одна и та же величина. Различие лишь в записи расчетной формулы.

Квадратическая простая

Средняя квадратическая простая вычисляется по формуле: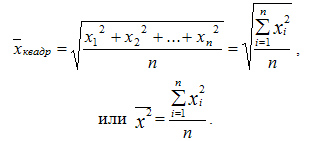



Квадратическая взвешенная

Средняя квадратическая взвешенная равна: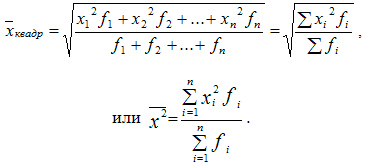


Вариационный ряд и его элементы

В каждой совокупности ее отдельные единицы отличаются друг от друга по величине изучаемого признака. Это различие называется вариацией.

Группировка единиц совокупности по величине варьирующего признака дает вариационные ряды. Вариационный ряд - это ряд числовых значений изучаемого признака. Каждый вариационный ряд включает в себя следующие элементы:

• варианта (V) - каждое отдельное числовое значение признака в совокупности (рост каждого ребенка, частота пульса каждого больного, число лейкоцитов в крови каждого обследованного и т.д.), в том числе Vmin - наименьшая варианта и Vmax - наибольшая варианта, ограничивающие вариационный ряд

• частота или математический вес (Р) - число, которое показывает, сколько раз данный признак (варианта) встречается в совокупности

• число наблюдений (n) - сумма всех частот ( n = ∑ P)

• интервал - разность между двумя соседними вариантами (V3-V2 , V2-V1, т.д.)

• амплитуда - разность между наибольшей и наименьшей вариантами (Vmax - Vmin)

• мода (Мо) - варианта, которая встречается в вариационном ряду наиболее часто (т.е. имеющая наибольшую частоту или наибольший математический вес)

• медиана (Ме) - величина, которая делит вариационный ряд на две равные части по числу наблюдений. Если число наблюдений четное, то место расположения середины вариационного ряда определяется по формуле n , если нечетное - n + 1 2 2



Виды вариационных рядов

* ранжированный (упорядоченный) ряд - такой, в котором числовые значения вариант располагаются последовательно, по убыванию или по нарастанию (5, 7, 8, 12, 26, 31, 38 и т.д.)

* неранжированный ряд - такой, в котором варианты располагаются беспорядочно (34, 6, 12, 45, 24, 7, 98 и т.д.)

* прерывный (дискретный) ряд - такой, в котором варианты выражены только целым числом и не могут иметь промежуточных значений (число детей в семье, число лейкоцитов в крови, частота пульса, число посещений, пр.)

* непрерывный ряд - такой, в котором варианты могут принимать любые значения, в том числе и дробные (рост, масса тела, время, затраченное на прием одного больного, содержание в крови или воздухе различных веществ, пр.)

* простой (развернутый) ряд - такой, в котором каждая варианта и соответствующая ей частота обозначены отдельно. Ряд, в котором каждая варианта встречается с частотой, равной единице, называется простым невзвешенным, а если с разной частотой - простым взвешенным.

* сгруппированный (интервальный) ряд - такой, в котором варианты соединены в группы, объединяющие их по величине в пределах определенного интервала.

Составление сгруппированного вариационного ряда

Простой, несгруппированный ряд, особенно при большом объеме совокупности, является громоздким и неудобным для вычисления средних величин, поэтому он обычно составляется при небольшом числе наблюдений (n ≤ 30). При большом числе наблюдений (n > 30) строят сгруппированный ряд на основе интервала (i), показывающего число вариант, объединенных в одну группу.

- Группировку рядов проводят следующим образом: Определяют размах ряда (амплитуду) вычитанием минимальной варианты из максимальной (Vmax - Vmin) Полученное число делят на желаемое количество групп - так определяется интервал. Начиная с минимальной варианты, строят вариационный ряд. Границы интервалов должны быть четкими, исключающими попадание одной и той же варианты в разные группы. Правильно составленный сгруппированный (интервальный) ряд должен отвечать следующим требованиям:

- Все варианты распределения должны войти в группы.

- Общее число выделенных групп должно быть не менее 7 (иначе вычисленная средняя арифметическая будет неточной) и не более 15 (иначе ряд будет большим и громоздким).

- Каждая новая последующая группа должна начинаться с новой последующей варианты, т.е. одна и та же варианта не должна встречаться в двух смежных группах.

- Интервал должен быть одинаковым в каждой группе, т.е. в каждую группу должно входить одинаковое число вариант.

- Размер интервала определяют, исходя из характера изучаемого признака, из числа выбранных групп, количества вариант и числа наблюдений.

- Величина интервала выбирается также с учетом целей и задач исследования.

- Каждая группа в сгруппированном ряду должна иметь начальную и конечную варианты, т.е. не должно быть так называемых открытых групп (например, до 5 лет, старше 60 лет и т.п.). Каждой группе присваивается частота, равная сумме частот всех вариант, вошедших в группу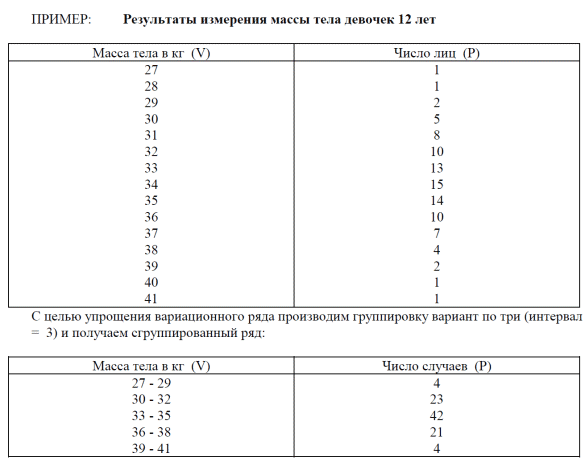



Дальнейшее упрощение сгруппированного ряда заключается в предварительном определении середины интервала (центральной варианты). В прерывных сгруппированных вариационных рядах центральная варианта определяется как полусумма начальной и конечной вариант в группе и ей присваивается суммарная частота всех вариант, вошедших в данную группу:



В непрерывных сгруппированных вариационных рядах центральная варианта определяется как полусумма начальных вариант соседних групп.



Занятие 4.