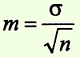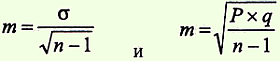Организация медикосоциального исследования. Статистические таблицы
 Скачать 1.91 Mb. Скачать 1.91 Mb.
|
Тема: «Параметрические методы оценки и анализа статистических гипотез»Применяя метод оценки достоверности результатов исследования для изучения общественного здоровья и деятельности учреждений здравоохранения, а также в своей научной деятельности, исследователь должен уметь правильно выбрать способ данной оценки. Среди методов оценки достоверности различают параметрические и непараметрические методы. Параметрическими называют количественные методы статистической обработки данных, применение которых требует обязательного знания закона распределения изучаемых признаков в совокупности и вычисления их основных параметров. В тех случаях, когда имеется малое количество наблюдений и характер распределения неизвестен, когда кроме количественных характеристик, результаты выражаются полуколичественными, а иногда описательными характеристиками (тяжесть заболевания, интенсивность реакции, результаты лечения), параметрические методы становятся непригодными. В этих ситуациях следует использовать непараметрические методы оценки достоверности. Непараметрическими являются количественные методы статистической обработки данных, применение которых не требует знания за кона распределения изучаемых признаков в совокупности и вычисления их основных параметров. В то же время следует отметить, что назначение применения непараметрических методов гораздо шире, чем только оценка достоверности результатов исследования (в том числе они применяются и для характеристики одной выборочной совокупности, и для изучения связи между явлениями). В данном случае акцент сделан на оценке достоверности результатов исследования, как одном из наиболее важных разделов статистического анализа, поэтому непараметрические методы не представлены отдельной главой. Как параметрические, так и непараметрические методы, используемые для сравнения результатов исследований, т.е. для сравнения выборочных совокупностей, заключаются в применении определенных формул и расчете определенных показателей в соответствии с предписанными для того или иного метода алгоритмами. В конечном результате высчитывается определенная числовая величина, которую сравнивают с табличными пороговыми значениями. Критерием достоверности будет результат сравнения полученной величины и табличного значения при данном числе наблюдений (или степеней свободы) и при заданном уровне безошибочного прогноза. Таким образом, в статистической процедуре оценки основное значение имеет полученный критерий достоверности, поэтому сам способ оценки достоверности в целом иногда называют тем или иным критерием по фамилии автора, предложившего его в качестве основы метода.
При проведении выборочных исследований полученный результат не обязательно совпадает с результатом, который мог бы быть получен при исследовании всей генеральной совокупности. Между этими величинами существует определенная разница, называемая ошибкой репрезентативности, т.е. это погрешность, обусловленная переносом результатов выборочного исследования на всю генеральную совокупность.
Формулы определения доверительных границ представлены следующим образом: для средних величин (М): Мген = Мвыб ± tm для относительных показателей (Р): Рген = Рвыб ± tm где Мген и Рген — соответственно, значения средней величины и относительного показателя генеральной совокупности; Мвы6 и Рвы6 — значения средней величины и относительного показателя выборочной совокупности; m — ошибка репрезентативности; t — критерий достоверности (доверительный коэффициент). Данный способ применяется в тех случаях, когда по результатам выборочной совокупности необходимо судить о размерах изучаемого явления (или признака) в генеральной совокупности. Обязательным условием для применения способа является репрезентативность выборочной совокупности. Для переноса результатов, полученных при выборочных исследованиях, на генеральную совокупность необходима степень вероятности безошибочного прогноза (Р), показывающая, в каком проценте случаев результаты выборочных исследований по изучаемому признаку (явлению) будут иметь место в генеральной совокупности. При определении доверительных границ средней величины или относительного показателя генеральной совокупности, исследователь сам задает определенную (необходимую) степень вероятности безошибочного прогноза (Р). Для большинства медико-биологических исследований считается достаточной степень вероятности безошибочного прогноза, равная 95%, а число случаев генеральной совокупности, в котором могут наблюдаться отклонения от закономерностей, установленных при выборочном исследовании, не будут превышать 5%. При ряде исследований, связанных, например, с применением высокотоксичных веществ, вакцин, оперативного лечения и т.п., в результате чего возможны тяжелые заболевания, осложнения, летальные исходы, применяется степень вероятности Р = 99,7%, т.е. не более чем у 1% случаев генеральной совокупности возможны отклонения от закономерностей, установленных в выборочной совокупности. Заданной степени вероятности (Р) безошибочного прогноза соответствует определенное, подставляемое в формулу, значение критерия t, зависящее также и от числа наблюдений. При n>30 степени вероятности безошибочного прогноза Р = 99,7% — соответствует значение t = 3, а при Р = 95,5% — значение t = 2. При п<30 величина t при соответствующей степени вероятности безошибочного прогноза определяется по специальной таблице (Н.А. Плохинского).
на определение ошибок репрезентативности (m) и доверительных границ средней величины генеральной совокупности (Мген) при числе наблюдений больше 30 Условие задачи: при изучении комбинированного воздействия шума и низкочастотной вибрации на организм человека было установлено, что средняя частота пульса у 36 обследованных водителей сельскохозяйственных машин через 1 ч работы составила 80 ударов в 1 минуту; σ = ± 6 ударов в минуту. Задание: определить ошибку репрезентативности (mM) и доверительные границы средней величины генеральной совокупности (Мген). Решение. Вычисление средней ошибки средней арифметической (ошибки репрезентативности) (m): m = σ / √n = 6 / √36 = ±1 удар в минуту Вычисление доверительных границ средней величины генеральной совокупности (Мген). Для этого необходимо: а) задать степень вероятности безошибочного прогноза (Р = 95 %); б) определить величину критерия t. При заданной степени вероятности (Р=95%) и числе наблюдений меньше 30 величина критерия t, определяемого по таблице, равна 2 (t = 2). Тогда Мген = Мвыб ± tm = 80 ± 2x1 = 80 ± 2 удара в минуту. Вывод. Установлено с вероятностью безошибочного прогноза Р = 95%, что средняя частота пульса в генеральной совокупности, т.е. у всех водителей сельскохозяйственных машин, через 1 ч работы в аналогичных условиях будет находиться в пределах от 78 до 82 ударов в минуту, т.е. средняя частота пульса менее 78 и более 82 ударов в минуту возможна не более, чем у 5% случаев генеральной совокупности.
на определение ошибок репрезентативности (m) и доверительных границ относительного показателя генеральной совокупности (Рген) Условие задачи: при медицинском осмотре 164 детей 3 летнего возраста, проживающих в одном из районов городе Н., в 18% случаев обнаружено нарушение осанки функционального характера. Задание: определить ошибку репрезентативности (mp) и доверительные границы относительного показателя генеральной совокупности (Рген). Решение. Вычисление ошибки репрезентативности относительного показателя: m = √P x q / n = √18 x (100 - 18) / 164 = ± 3% Вычисление доверительных границ средней величины генеральной совокупности (Рген) производится следующим образом: необходимо задать степень вероятности безошибочного прогноза (Р=95%); при заданной степени вероятности и числе наблюдений больше 30, величина критерия t равна 2 (t = 2). Тогда Рген = Рвыб± tm = 18% ± 2 х 3 = 18% ± 6%. Вывод. Установлено с вероятностью безошибочного прогноза Р=95%, что частота нарушения осанки функционального характера у детей 3 летнего возраста, проживающих в городе Н., будет находиться в пределах от 12 до 24% случаев.
Данный способ применяется в тех случаях, когда необходимо определить, случайны или достоверны (существенны), т.е. обусловлены какой-то причиной, различия между двумя средними величинами или относительными показателями. Обязательным условием для применения данного способа является репрезентативность выборочных совокупностей, а также наличие причинно-следственной связи между сравниваемыми величинами (показателями) и факторами, влияющими на них. Формулы определения достоверности разности представлены следующим образом: 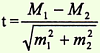 для средних величин 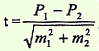 для относительных показателей где t — критерий достоверности, m1 и m2 — ошибки репрезентативности, М1 и М2 — средние величины, Р1 и Р2 — относительные показатели. Если вычисленный критерий t более или равен 2 (t ≥ 2), что соответствует вероятности безошибочного прогноза Р равном или более 95% (Р ≥ 95%), то разность следует считать достоверной (существенной), т.е. обусловленной влиянием какого-то фактора, что будет иметь место и в генеральной совокупности. При t < 2, вероятность безошибочного прогноза Р < 95%, это означает, что разность недостоверна, случайна, т.е. не обусловлена какой-то закономерностью (не обусловлена влиянием какого-то фактора). Поэтому полученный критерий должен всегда оцениваться по отношению к конкретной цели исследования. Занятие 5. | ||||||||||||||