Организация медикосоциального исследования. Статистические таблицы
 Скачать 1.91 Mb.
|
Тема: «Анализ взаимосвязи между исследуемыми параметрами статистических совокупностей»Важнейшей целью статистики является изучение объективно существующих связей между явлениями. В ходе статистического исследования этих связей необходимо выявить причинно-следственные зависимости между показателями, т.е. насколько изменение одних показателей зависит от изменения других показателей. Существует две категории зависимостей (функциональная и корреляционная) и две группы признаков (признаки-факторы и результативные признаки). В отличие от функциональной связи, где существует полное соответствие между факторными и результативными признаками, в корреляционной связи отсутствует это полное соответствие. Корреляционная связь- это связь, где воздействие отдельных факторов проявляется только как тенденция (в среднем) при массовом наблюдении фактических данных. Примерами корреляционной зависимости могут быть зависимости между размерами активов банка и суммой прибыли банка, ростом производительности труда и стажем работы сотрудников. Корреляционно-регрессионный метод анализа Наиболее простым вариантом корреляционной зависимости является парная корреляция, т.е. зависимость между двумя признаками (результативным и факторным или между двумя факторными). Математически эту зависимость можно выразить как зависимость результативного показателя у от факторного показателя х. Связи могут быть прямые и обратные. В первом случае с увеличением признака х увеличивается и признак у, при обратной связи с увеличением признака х уменьшается признак у. Важнейшей задачей является определение формы связи с последующим расчетом параметров уравнения, или, иначе, нахождение уравнения связи (уравнения регрессии). Могут иметь место различные формы связи: прямолинейная  криволинейная в виде: параболы второго порядка (или высших порядков)  гиперболы  показательной функции  и т.д. Параметры для всех этих уравнений связи, как правило, определяют из системы нормальных уравнений, которые должны отвечать требованию метода наименьших квадратов (МНК):   (Если связь выражена параболой второго порядка ( 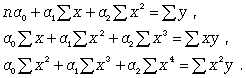 ), то систему нормальных уравнений для отыскания параметров a0 , a1 , a2 (такую связь называют множественной, поскольку она предполагает зависимость более чем двух факторов) можно представть в виде Другая важнейшая задача - измерение тесноты зависимости - для всех форм связи может быть решена при помощи вычисления эмпирического корреляционного отношения 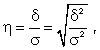 : где - 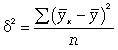 дисперсия в ряду выравненных значений результативного показателя  ;  - 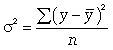дисперсия в ряду фактических значений у.Для определения степени тесноты парной линейной зависимости служит линейный коэффициент корреляции r, для расчета которого можно использовать, например, две следующие формулы: 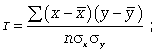 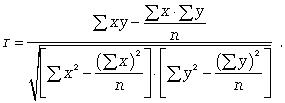 Линейный коэффициент корреляции может принимать значения в пределах от -1 до + 1 или по модулю от 0 до 1. Чем ближе он по абсолютной величине к 1, тем теснее связь. Знак указывает направление связи: «+» - прямая зависимость, «-» имеет место при обратной зависимости. Непараметрические показатели связи В статистической практике могут встречаться такие случаи, когда качества факторных и результативных признаков не могут быть выражены численно. Поэтому для измерения тесноты зависимости необходимо использовать другие показатели. Для этих целей используются так называемые непараметрические методы. Наибольшее распространение имеют ранговые коэффициенты корреляции, в основу которых положен принцип нумерации значений статистического ряда. При использовании коэффициентов корреляции рангов коррелируются не сами значения показателей х и у, а только номера их мест, которые они занимают в каждом ряду значений. В этом случае номер каждой отдельной единицы будет ее рангом. Коэффициенты корреляции, основанные на использовании ранжированного метода, были предложены К. Спирмэном и М. Кендэлом. Коэффициент корреляции рангов Спирмэна(р) основан на рассмотрении разности рангов значений результативного и факторного признаков и может быть рассчитан по формуле 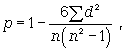 где d = Nx - Ny , т.е. разность рангов каждой пары значений х и у; n - число наблюдений. Ранговый коэффициент корреляции Кендэла( 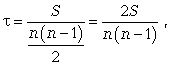 ) можно определить по формуле где S = P + Q. К непараметрическим методам исследования можно отнести коэффициент ассоциации Кас и коэффициент контингенции Ккон , которые используются, если, например, необходимо исследовать тесноту зависимости между качественными признаками, каждый из которых представлен в виде альтернативных признаков. Для определения этих коэффициентов создается расчетная таблица (таблица «четырех полей»), где статистическое сказуемое схематически представлено в следующем виде:
Здесь а, b, c, d - частоты взаимного сочетания (комбинации) двух альтернативных признаков  ; n - общая сумма частот.Коэффициент ассоциации можно расcчитать по формуле  Коэффициент контингенции рассчитывается по формуле 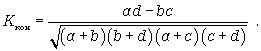 Нужно иметь в виду, что для одних и тех же данных коэффициент контингенции (изменяется от -1 до +1) всегда меньше коэффициента ассоциации. Если необходимо оценить тесноту связи между альтернативными признаками, которые могут принимать любое число вариантов значений, применяется коэффициент взаимной сопряженности Пирсона (КП ). Для исследования такого рода связи первичную статистическую информацию располагают в форме таблицы:
Здесь mij - частоты взаимного сочетания двух атрибутивных признаков; П - число пар наблюдений. Коэффициент взаимной сопряженности Пирсонаопределяется по формуле 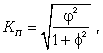 где 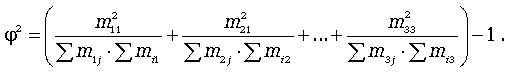 - показатель средней квадратической сопряженности: Коэффициент взаимной сопряженности изменяется от 0 до 1. Наконец, следует упомянуть коэффициент Фехнера, характеризующий элементарную степень тесноты связи, который целесообразно использовать для установления факта наличия связи, когда существует небольшой объем исходной информации. Данный коэффициент определяется по формуле  где na - количество совпадений знаков отклонений индивидуальных величин от их средней арифметической; nb - соответственно количество несовпадений. Коэффициент Фехнера может изменяться в пределах -1,0  Кф +1,0.Занятие 6. |