Основные требования к знаниям, умениям и навыкам учащихся
 Скачать 1.98 Mb. Скачать 1.98 Mb.
|
|
Ф и з к у л ь т м и н у т к а Раз, два – выше голова, Три, четыре – руки шире, Пять, шесть – тихо сесть, Семь, восемь – лень отбросим. Раз – согнуться, разогнуться, Два – нагнуться, потянуться, Три – в ладоши три хлопка, Головою три кивка. На четыре – руки шире, Пять, шесть – тихо сесть, Семь, восемь – лень отбросим. IV. Работа над пройденным материалом. 1. Решение задач. Перед выполнением задания № 2 учитель должен вспомнить с учащимися взаимосвязь между величинами: цена, количество, стоимость. Учитель. Как найти цену, если известны количество и стоимость? Дети. Надо стоимость разделить на количество. Учитель. Как найти количество, если известны цена и стоимость? Дети. Надо стоимость разделить на цену. Учитель. Как найти стоимость, если известны цена и количество? Дети. Надо цену умножить на количество. После этого записывают в таблицу условие задачи, и дети решают задачу самостоятельно. В задании № 3 учащиеся самостоятельно составляют и решают задачу с последующей проверкой. В задании № 4 два вопроса. Можно предложить учащимся I варианта ответить на первый вопрос, а учащиеся II варианта отвечают на второй вопрос. Дети решают задачу самостоятельно. Учитель помогает учащимся, которые затрудняются в записи условия или решения задачи. После этого проводится проверка. 2. Для самостоятельной работы на уроке можно предложить решить уравнение № 5. V. Итоги урока. Учитель. Ребята, что нового мы сегодня узнали на уроке? Дети. Сегодня на уроке мы составляли таблицу умножения и деления с числом 4. Учитель. Что повторяли на уроке? Дети. На уроке повторяли задачи, решали уравнения. Домашнее задание: с. 48, № 5. У р о к 38. ПЕРИМЕТР ПРЯМОУГОЛЬНИКА (с. 49) Цели: познакомить учащихся с различными способами нахождения периметра прямоугольника; продолжить работу по закреплению табличных случаев умножения и деления с числами 2, 3, 4. Ход урока I. Организационный момент. II. Устный счёт. 1. В устную работу на уроке с целью закрепления изученных случаев умножения и деления можно включить задание № 5: : = 8. – Подберите по два значения делимого и делителя, чтобы значение частного равнялось 8. (24 : 3 = 8, 32 : 4 = 8). В задании № 7 учащиеся выясняют, что каждое последующее число увеличивается на 3. Значит, следующие числа 18, 21, 24. З а д а н и е № 8. Найдите значение выражений а 3 и а 4. Учащиеся подставляют данные значения переменной и говорят ответы: при а = 5, а = 6, а = 8, а = 9. 2. При работе над геометрическим материалом устно можно разобрать задание «Сравни периметры фигур» (на полях учебника). Дети измеряют стороны фигур, находят периметр: Р1 = 2 + 2 + 2 + 2 = 8 (см) или Р1 = 2 · 4 = 8 (см) Р2 = 2 · 4 = 8 (см) Р3 = 2 + 2 + 2 = 6 (см) или Р3 = 2 · 3 = 6 (см) Учащиеся делают вывод: периметры фигур № 1 и № 2 одинаковые. Периметр треугольника самый маленький по сравнению с периметром других фигур. При разборе головоломки (в самом низу страницы) ученики измеряют стороны треугольника, находят его периметр: РД = 6 + 2 + 7 = 15 (см). После этого находят длину стороны пятиугольника: 15 : 5 = 3 (см). III. Работа над новым материалом. В качестве подготовки к рассмотрению нового необходимо вспомнить то, что детям уже известно о прямоугольнике (четырехугольник, у которого все углы прямые). Полезно спросить, сколько у прямоугольника углов, сторон, вершин. Отвечая на эти вопросы, ученикам следует найти на чертеже (предварительно учитель делает на доске чертеж) прямоугольника его элементы. Учитель. Ребята, для того чтобы начертить прямоугольник, что нам надо знать? Дети. Нам надо знать его длину и ширину. Учитель. А почему надо знать длину только двух сторон, а не всех четырёх? Дети. Потому что у прямоугольника противоположные стороны равны. Учитель. Покажите на чертеже, где у прямоугольника противоположные стороны. Дети выходят к доске и показывают. Затем учащиеся обращаются к чертежу в учебнике на с. 49 (вверху). Дети читают задачу, рассматривают чертеж и пытаются объяснить новые способы нахождения периметра. Объяснения могут быть примерно такие: 2 · 2 + 3 · 2. У данного прямоугольника две стороны по 2 см и две стороны по 3 см. Поэтому 2 · 2 и 3 · 2, а затем полученные результаты складывают. В записи (2 + 3) · 2 сначала складывают длину с шириной, а затем умножают эту сумму на 2. После разбора учащиеся делают такой же чертеж в тетради и записывают два новых способа решения и ответ. Необходимо выяснить, какой способ решения рациональнее. Учитель. Ребята, мы нашли периметр прямоугольника двумя способами. Как вы думаете, какой из них более рациональный, то есть удобный. Каким можно быстрее получить результат? Дети. Мы думаем, что второй, где сумма умножается на 2. Учитель. А почему? Дети. Потому что надо выполнить всего 2 действия, а в первом способе – 3 действия. С целью закрепления изученного выполняется задание № 1 с комментированием. № 1. Начертите прямоугольник со сторонами 4 см и 3 см. Найдите его периметр. Сначала дети чертят фигуру в своих тетрадях, а затем один из них комментирует: – Чтобы найти периметр прямоугольника, надо сложить его длину и ширину, а полученную сумму умножить на 2. Запись на доске: Р? = (3 + 4) · 2 = 14 (см) О т в е т: Р = 14 см. Перед решением задания № 2 учитель должен вспомнить с детьми, что они знают о квадрате. Квадрат – это прямоугольник, у которого все стороны равны. Далее проводится беседа. Учитель. Сколько сторон у квадрата? Дети. 4. Учитель. Какие это стороны? Дети. Все стороны одинаковые. Учитель. Если длина стороны квадрата 2 см, то как легко найти его периметр? Дети. Надо 2 умножить на 4. Учитель. Верно. Запишем решение: Р? = 2 · 4 = 8 (см). О т в е т: Р = 8 см. Аналогично находятся периметры еще двух квадратов. Ф и з к у л ь т м и н у т к а Мы становимся всё выше, Достаём руками крыши. На два счёта – поднялись, Три, четыре – руки вниз. IV. Работа над пройденным материалом. Для самостоятельной работы на уроке можно включить задания № 3, № 4, № 6. После решения задач № 3, № 4 на усмотрение учителя можно провести проверку. V. Итоги урока. Учитель. Ребята, что нового мы сегодня узнали на уроке? Дети. Сегодня на уроке мы познакомились с тем, как можно найти периметр прямоугольника разными способами; измеряли стороны и находили периметр других фигур. Учитель. Что закрепляли на уроке? Дети. Мы решали задачи, повторяли табличные случаи умножения и деления. Домашнее задание: с. 49, № 4, № 6. У р о к 39. ЗАКРЕПЛЕНИЕ ПРОЙДЕННОГО (с. 50) Цели: закреплять табличные случаи умножения и деления с числами 2, 3, 4; совершенствовать вычислительные навыки и умение решать задачи. Ход урока I. Организационный момент. II. Устный счёт. 1. Для закрепления навыков табличного умножения и деления с числами 2, 3, 4 включить задание № 1 (1, 2, 3). Дети по заданию записывают таблицу, а затем, пользуясь этой таблицей, устно выполняют задание № 2. 2. На доске записать примеры и попросить учащихся вставить нужные числа: ? · 8 = 24 7 · ? = 28 21 : ? = 7 24 : ? = 6 ? · 9 = 36 9 · ? = 27 20 : ? = 5 18 : ? = 9 3. Для закрепления навыков сложения и вычитания в пределах 100 предложить заполнить «магический квадрат»: 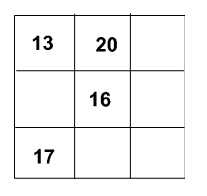 Сумма – 48. III. Работа над пройденным материалом. 1. Решение задач. При выполнении задания № 3 учитель вместе с детьми записывает условие задачи таблицей:
Далее дети решают задачу самостоятельно. Перед решением задачи № 4 учащиеся ставят вопрос: «Сколько всего минут передавали по радио сказку и концерт?». Прежде чем приступить к решению задания № 6, учащиеся вспоминают, как найти периметр квадрата. Учитель. Ребята, вспомните, что за фигура – квадрат? Учащиеся. Квадрат – это прямоугольник, у которого все стороны равны. Учитель. А сколько сторон у квадрата? Учащиеся. Четыре. Учитель. Как же мы найдём периметр квадрата? Учащиеся. Длину стороны умножим на 4. Затем записывают решение самостоятельно с последующей проверкой. 2. Для самостоятельной работы предложить задание № 5. Если на уроке останется время, можно разобрать задания на сообразительность на с. 51 № 1, № 2, № 3. IV. Итоги урока. Учитель. Что мы закрепляли сегодня на уроке? Дети. Сегодня мы повторяли табличные случаи умножения и деления с числами 2, 3, 4; решали задачи, находили периметры геометрических фигур. Домашнее задание: с. 50, № 5. У р о к 40. КОНТРОЛЬНАЯ РАБОТА ЗА I ЧЕТВЕРТЬ Цель: закрепить пройденный за I четверть материал. I вариант 1. Мама купила 3 пакета картофеля по 5 кг в каждом. Сколько килограммов картофеля купила мама? 2. 3 мальчика разделили поровну между собой 18 орехов. Сколько орехов получил каждый? 3. Решите уравнения: х + 36 = 56 х – 13 = 20 4. Решите примеры: 8 · 2 6 · 3 15 : 5 21 : 3 3 · 8 12 : 6 18 : 2 4 · 3 2 · 9 5. Найдите значение выражений: 60 – (24 + 3) : 3 = 24 : 3 + 9 · 2 = 6.* Я живу в семье с мамой, папой, бабушкой и дедушкой. Сколько тапочек для всех членов моей семьи должно быть у нас дома, если у каждого члена семьи будет по одной паре тапочек? II вариант 1. В телевикторине участвовали 3 команды по 6 человек в каждой. Сколько всего человек участвовало в этой телевикторине? 2. Из 24 кубиков Лена построила 3 одинаковые башни. Сколько кубиков в каждой башне? 3. Решите уравнения: х + 48 = 96 х – 23 = 8 4. Решите примеры: 12 : 3 8 · 2 24 : 8 5 · 3 18 : 3 3 · 7 14 : 2 2 · 5 27 : 9 5. Найдите значение выражений: (71 – 65) · 3 18 : 3 + 8 · 2 6.* За столом сидела вся наша семья: я, мама, папа, брат и бабушка. Каждый из нас съел по 2 пирожка. На сколько меньше стало пирожков? * Задачи на смекалку. У р о к 41. РАБОТА НАД ОШИБКАМИ. ЗАКРЕПЛЕНИЕ ПРОЙДЕННОГО На этом уроке учитель даёт анализ проведённой контрольной работы, проводит с учащимися работу над ошибками в тех заданиях, где было допущено их больше всего, подбирает похожие задания, чтобы отработать необходимые навыки и умения. У р о к 42. РЕШЕНИЕ ЗАДАЧ НА НАХОЖДЕНИЕ ЧИСЛА, КОТОРОЕ В НЕСКОЛЬКО РАЗ БОЛЬШЕ ДАННОГО (с. 52) Цели: познакомить учащихся с новым видом задач на увеличение числа в несколько раз; закреплять умение решать уравнения и находить значения выражений с переменной, а также вспомнить правила умножения чисел 1 и 0. Ход урока I. Организационный момент. II. Устный счёт. 1. «Цепочка»: 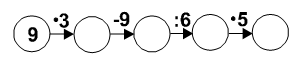 2. Выполните действия и сравните: 3 · 8 – 20 : 4 (3 · 8 – 20) : 4 (3 + 24) : 3 3 + 24 : 3 12 : 6 · 2 12 : (6 · 2) 36 : 9 + 3 · 2 (36 : 9 + 3) · 2 III. Работа над новым материалом. Сначала надо раскрыть смысл выражения «в 2 (3, 4…) раза больше» с помощью наглядных пособий. Целесообразно выполнить ряд упражнений, подобных следующим: 1) Учитель. Положите слева 4 кружка, а справа 2 раза по 4 кружка. В таком случае говорят, что справа кружков в 2 раза больше, чем слева, потому что там 2 раза по столько кружков, сколько их слева; слева в 2 раза меньше, чем справа – там один раз 4 кружка. 2) Учитель. Положите слева 2 квадрата, а справа 3 раза по 2 квадрата. Что можно сказать о числе квадратов справа: их больше или меньше, чем слева? Дети. Их в 3 раза больше, чем слева, а слева в 3 раза меньше, чем справа. 3) Учитель. Положите справа 3 треугольника, а слева в 4 раза больше. Что это значит? Дети. По 3 треугольника взять 4 раза. Учитель. Что можно сказать о числе треугольников справа: их больше или меньше, чем слева? Дети. Их в 4 раза меньше. После этого ученики рассматривают в учебнике рисунок (в самом верху) с кружками и читают объяснение. Учитель. Как узнать, сколько синих кружков? Ученик. Чтобы получить в 4 раза больше, чем 3, надо по 3 взять 4 раза или 3 умножить на 4, получится 12. Запишу: 3 · 4 = 12. О т в е т: 12 кружков. Для закрепления надо решить задачу № 1 под руководством учителя: после чтения задачи дети объясняют, что значит в 3 раза больше, выполняют рисунок. Учитель также показывает, как записать краткое условие задачи.  Зеленых – 5 м. Красных – ?, в 3 раза б. Далее выполняется решение. Выбор арифметического действия дети объясняют так: красных мячей было в 3 раза больше, чем зеленых, значит, их было 3 раза по 5, надо 5 умножить на 3. 5 · 3 = 15 (м.) О т в е т: 15 красных мячей. После решения учитель спрашивает: – Что можно сказать о числе зеленых мячей – их больше или меньше, чем красных, и во сколько раз? Учащиеся. Их меньше в 3 раза. Такие вопросы помогут детям в дальнейшем осмыслить суть выражения «меньше в …». Аналогично разбирается задание № 2 с комментированием. Ф и з к у л ь т м и н у т к а А теперь насос включаем, Воду из реки качаем. Влево – раз, вправо – два, Потекла ручьём вода. Раз, два, три, четыре – Хорошо мы потрудились. (3 раза.) (И. П. – стойка: ноги врозь; 1 – наклон влево, правая рука скользит вверх вдоль туловища (до подмышечной впадины); 2 – И. П.; 3 – наклон вправо, движение вверх левой рукой; 4 – И. П.) IV. Работа над пройденным материалом. Для самостоятельной работы на уроке предложить учащимся задание № 3 (1, 2). Поставив нужное число в условие первой задачи, дети ее решают, а потом составляют и решают две обратные к ней задачи с последующей проверкой. Перед выполнением задания № 5 желательно вспомнить с учащимися правила умножения с числами 1 и 0. Если 1 умножить на любое число, то получится то число, на которое умножали. При умножении 0 на любое число получится всегда 0. После этого дети работают самостоятельно. Задания № 4 и № 6 также не вызывают затруднений у учащихся, и потому они выполняются самостоятельно. V. Итоги урока. Учитель. Ребята, что нового мы сегодня узнали на уроке? Дети. Сегодня на уроке мы познакомились с новым видом задач: учились правильно записывать условие и решение. Учитель. Что повторяли на уроке? Дети. На уроке мы вспомнили решение уравнений, находили значение выражения с переменной. Домашнее задание: с. 52, № 4, № 6. У р о к 43. ЗАКРЕПЛЕНИЕ ПРОЙДЕННОГО (с. 53) Цели: закрепить умение решать задачи на увеличение числа в несколько раз и сопоставить эти задачи с задачами на увеличение числа на несколько единиц; продолжить решение задач, связанных с вычислением периметра прямоугольника; закреплять изученные табличные случаи умножения и деления. Ход урока I. Организационный момент. II. Устный счёт. Для закрепления знания рассмотренных таблиц умножения и деления включить соответствующие примеры, используя игры. а) Игра «Лесенка»:
б) Сравните: 5 + 3 … 5 · 3 6 · 4 … 4 · 6 2 + 2 … 2 · 2 7 + 7 … 7 · 3 8 ·2 … 8 · 3 9 + 9 … 9 · 2 в) Назовите числа от 4 до 30, которые делятся без остатка на 3, на 4. г) Вычислите, применяя правила порядка выполнения арифметических действий: (54 – 46) · 2 8 · 4 – 20 : 4 (15 + 6) : 3 4 · 7 + 36 : 9 40 : 10 · 8 28 : (7 – 3) |
