Основные требования к знаниям, умениям и навыкам учащихся
 Скачать 1.98 Mb. Скачать 1.98 Mb.
|
|
Цели: познакомить учащихся со взаимосвязью между компонентами и результатом умножения; продолжать работу по закреплению умения решать простые задачи на умножение и деление; совершенствовать навыки решения уравнений и примеров. Ход урока I. Организационный момент. II. Устный счёт. 1. Найдите лишние числа: а) 90, 20, 25, 50, 70; б) 42, 24, 48, 45, 49; в) 76, 32, 18, 4, 27. 2. Сравните: 27 … 29 5 дм … 50 см 76 … 56 3 дм 2 см … 2 дм 3 см 94 … 49 7 дм 4 см … 48 см III. Работа над новым материалом. Для разъяснения взаимосвязи между множителями и произведением учитель записывает на доске пример на умножение: 7 · 4. Дети читают этот пример с использованием терминов «первый множитель», «второй множитель», вычисляют с помощью сложения произведение. Учитель записывает ответ, названия компонентов и результата. 1-й множитель 2-й множитель Произведение 7 · 4 = 28 28 : 7 = 4 28 : 4 = 7 Выясняя, как получены второй и третий примеры из первого, дети приходят к выводу, что, разделив произведение (28) на первый множитель (7), получили второй множитель (4), а разделив произведение (28) на второй множитель (4), получили первый множитель (7). Учитель. Ребята, посмотрите на запись второго примера. Как его получили из первого? Дети. Произведение 28 разделили на первый множитель 7 и получили второй множитель 4. Учитель. А как получили третий пример из первого? Дети. Произведение 28 разделили на второй множитель 4 и получили первый множитель 7. Затем аналогичная работа проводится по рисункам и записям, данным вверху на с. 27 учебника. При этом полезно попросить объяснить записи с использованием данных в учебнике рисунков. 2 · 5 = 10 3 · 4 = 12 10 : 2 = 5 12 : 3 = 4 10 : 5 = 2 12 : 4 = 3 (Объяснения будут такими же, как и в предыдущем примере.) Наконец, дети читают текст в красной рамке, и учитель говорит, что этот вывод следует запомнить. Если произведение двух множителей разделить на один из них, то получится другой множитель. Затем выполняют с пояснением задание № 1. При выполнении этого упражнения надо объяснить, как можно решить нижний пример на деление, опираясь на решение примера на умножение, записанного над ним. Учащиеся, пользуясь изученным выводом, решают примеры: 7 · 4 = 28 28 : 7 = 4 Учащиеся. Во втором примере произведение 28 разделили на первый множитель 7. Значит, получится второй множитель 4. Ф и з к у л ь т м и н у т к а Мы становимся всё выше, Достаём руками крыши. На два счёта – поднялись, Три, четыре – руки вниз. IV. Работа над пройденным материалом. 1. Решение задач. Работа над заданием № 2 проводится аналогично работе на уроке № 20, задание № 1. Задание № 4 сначала разбирается вместе с учителем. Прочитав его, дети увидят, что условие должно быть дополнено числовыми данными. Учащиеся подставляют числа и после этого самостоятельно решают задачу. Было – 56 т Израсходовал – 10 т и ещё 12 т Осталось – ? 1) 10 + 12 = 22 (т) – израсходовал 2) 56 – 22 = 34 (т) О т в е т: 34 тетради осталось. 2. Работа над геометрическим материалом. Выполняя задание № 5, учащиеся рассматривают рисунки на полях. На первом чертеже ученики должны найти и записать название трех отрезков: АВ, АС, СВ. На втором чертеже находят 3 треугольника: КМО, КМТ, ТМО. На третьем чертеже 5 треугольников: АВМ, МВК, КСМ, МСД, ВСМ. 3. Для самостоятельной работы учащимся предлагаются задания № 3, № 6, № 7. V. Итоги урока. Учитель. Ребята, что нового узнали сегодня на уроке? Дети. На уроке мы рассмотрели взаимосвязь между компонентами и результатом умножения. Учитель. Какую же связь мы установили? Дети. Если произведение разделить на один из множителей, то получится другой множитель. Учитель. Что ещё повторяли на уроке? Дети. Сравнивали числа и единицы длины, решали уравнения и примеры, находили на чертежах нужные геометрические примеры. Домашнее задание: с. 27, № 6, № 7. У р о к 22. СВЯЗЬ ДЕЛЕНИЯ С УМНОЖЕНИЕМ (с. 28) Цели: продолжать работу над раскрытием связи деления с умножением; закреплять умения решать уравнения, примеры и задачи. Ход урока I. Организационный момент. II. Устный счёт. 1. «Лабиринт» (рисунок был до урока нарисован на доске). – Проходя «ворота», складывайте числа.  2. Решите арифметические ребусы: +…7 _… … _ 5 4 +…7 1 … 2 5 …8 5 … 6 5 6 0 3 … 9 1 III. Повторение пройденного материала. 1. Рассмотреть задание № 1. Дети рассматривают первый рисунок.  Учитель (проводит беседу). Сколько кружков в первом ряду? Дети. 4. Учитель. А сколько во втором ряду? Дети. 4. Учитель. Как узнать, сколько всего кружков? Дети. 4 · 2 = 8. Учитель. Прочитайте этот пример, используя названия чисел при умножении. Дети. 4 – первый множитель, 2 – второй множитель, 8 – произведение. Учитель. А как можно еще по-другому узнать, сколько всего кружков? Дети. 2 · 4 = 8. Учитель. Почему мы можем сделать такую запись? Дети. От перестановки множителей произведение не изменяется. Учитель. 8 кружков вы разложили в 2 ряда поровну. Сколько кружков в каждом ряду? Дети. По 4 кружка. Учитель. Как посчитали? Дети. 8 : 2 = 4. Учитель. Сравните этот пример с первым. Что заметили? Дети. Произведение разделили на второй множитель и получили первый множитель. Учитель. Верно. А если 8 кружков разложить по 4 кружка в ряд, сколько получится рядов? Дети. 2 ряда. Учитель. Как посчитали? Дети. 8 : 4 = 2. Учитель. Сравните последний пример с первым. Что замечаете? Дети. Произведение разделили на первый множитель и получили второй множитель. Аналогичным образом провести работу по другим записям и рисункам. Только учащиеся рассказывают уже все сами. Выполняя задание № 2, учащиеся рассуждают: «40 : 8 = 5, потому что здесь произведение 40 разделили на первый множитель 8, значит, получится второй множитель 5». Для того чтобы выполнить задание № 4, дети должны сначала выполнить рисунок: 6 : 3 = 2 10 : 2 = 5 12 : 4 = 3 2. Решение задач. Прежде чем учащиеся приступят к самостоятельному решению задачи № 5, надо уточнить, на сколько равных частей делятся 20 орехов. Дети должны прийти к выводу: на 4 равные части. Задание № 6 выполняют самостоятельно с последующей проверкой. 3. Для самостоятельной работы учащимся можно предложить задания № 3, № 7, № 8 и № 9. IV. Итоги урока. Учитель. Что закрепляли сегодня на уроке? Дети. Сегодня на уроке закрепляли связь деления с умножением, решали задачи, уравнения и примеры. Учитель. Какие задания на уроке показались самыми интересными? Какие – не очень интересными? Домашнее задание: с. 28, № 7, № 8. У р о к 23. УМНОЖЕНИЕ И ДЕЛЕНИЕ С ЧИСЛОМ 10 (с. 29) Цели: познакомить учащихся с приемами умножения и деления с числом 10, основанных на взаимосвязи умножения и деления; научить использовать изученный прием при решении задач и примеров. Ход урока I. Организационный момент. II. Устный счёт. 1. Заполните «Занимательную рамку».
2. Арифметический диктант. – На сколько 90 больше 75? – Уменьшаемое 47, вычитаемое 15. Найдите разность. – Уменьшите 67 на 20. – Увеличьте 32 на 7. – Найдите разность чисел 60 и 4. – Найдите сумму чисел 36 и 8. – Первое слагаемое 18, второе 17. Чему равна сумма? III. Работа над новым материалом. Работу на уроке можно начать с рассмотрения задачи и рисунка к ней вверху на с. 29. После чтения задачи учитель проводит беседу: – Как узнать, сколько кубиков в 2 пакетиках? Дети. Надо 10 умножить на 2. Учитель. Как посчитать, сколько получится? Дети. 10 + 10 = 20. Учитель. Значит, 10 · 2 = 20. А если применить переместительное свойство умножения, то какой пример можно записать? Дети. 2 · 10 = 20. Учитель. Хорошо. А как умножение связано с делением? Дети. Если произведение разделить на один из множителей, то получится другой множитель. Учитель. Какие примеры на деление можно составить, используя наш пример на умножение? Дети. 20 : 10 = 2 и 20 : 2 = 10. Учитель на доску выносит запись: 10 · 2 = 20 2 · 10 = 20 20 : 10 = 2 20 : 2 = 10 Аналогичная работа проводится, когда дети отвечают на вопрос: «Сколько кубиков в 4 пакетах?». В результате рассуждений на доске появляется запись: 10 · 4 = 40 4 · 10 = 40 40 : 10 = 4 40 : 4 = 10 Для закрепления изученного выполняется задание № 1. Учитель с учащимися разбирает, что в первом столбике пример на умножение устно заменяется примером на сложение и находится результат. Значение примеров во втором столбике находится при применении переместительного свойства умножения. Результаты примеров третьего и четвертого столбиков находятся по правилу:если произведение разделить на один из множителей, то получится другой множитель. В результате выполнения этого получится полностью таблица умножения и деления с числом 10. 10 · 3 = 30 3 · 10 = 30 30 : 3 = 10 30 : 10 = 3 10 · 4 = 40 4 · 10 = 40 40 : 4 = 10 40 : 10 = 4 10 · 5 = 50 5 · 10 = 50 50 : 5 = 10 50 : 10 = 5 10 · 6 = 60 6 · 10 = 60 60 : 6 = 10 60 : 10 = 6 10 · 7 = 70 7 · 10 = 70 70 : 7 = 10 70 : 10 = 7 10 · 8 = 80 8 · 10 = 80 80 : 8 = 10 80 : 10 = 8 10 · 9 = 90 9 · 10 = 90 90 : 9 = 10 90 : 10 = 9 10 · 10 = 100 10 · 10 = 100 100 : 10 = 10 100 : 10 = 10 Пользуясь полученной таблицей, учащиеся выполняют задание № 2. Дети находят на таблице нужный пример и говорят результат. Ф и з к у л ь т м и н у т к а Раз, два – выше голова, Три, четыре – руки шире, Пять, шесть – тихо сесть, Семь, восемь – лень отбросим. Раз – согнуться, разогнуться, Два – нагнуться, потянуться, Три – в ладоши три хлопка, Головою три кивка. На четыре – руки шире, Пять, шесть – тихо сесть, Семь, восемь – лень отбросим. IV. Работа над пройденным материалом. 1. Решение задач. Решая задачи № 3 и № 4 с комментированием у доски, учащиеся могут пользоваться составленной таблицей. № 3: Разложили – 50 б. на 5 т. На 1 тарелке – ? 50 : 5 = 10 (б.) О т в е т: 10 бутербродов на 1 тарелке. Учащийся ведёт запись на доске и всё это проговаривает вслух. 2. В самостоятельную работу на уроке можно включить задание № 5. V. Итоги урока. Учитель. Что нового узнали на уроке? Дети. Сегодня на уроке мы учились делить и умножать на число 10. Учитель. Что повторили на уроке? Дети. Повторили решение примеров на сложение и вычитание, решали задачи на умножение и деление. Домашнее задание: с. 29, № 5. У р о к 24. ПЕРИМЕТР МНОГОУГОЛЬНИКА (с. 30) Цели: познакомить учащихся с понятием периметра; научить находить периметр фигур; продолжать работу над решением задач, уравнений и примеров на умножение и деление с числом 10. Ход урока I. Организационный момент. II. Устный счёт. 1. Пользуясь результатом первого примера, найдите результат двух других примеров: 7 · 8 = 56 8 · 9 = 72 6 · 5 = 30 56 : 7 = 72 : 8 = 30 : 5 = 56 : 8 = 72 : 9 = 30 : 6 = 2. «Какое число следующее?».  Здесь учащиеся должны догадаться, что с каждым разом прибавляется число на единицу больше; сначала к 1 + 5 = 6, 6 + 6 = 12, 12 + 7 = 19, 19 + 8 = 27, 27 + 9 = 36, 36 + 10 = 46, 46 + 11 = 57. 3. Арифметические ребусы: III. Работа над новым материалом. Учитель на доске чертит прямоугольный треугольник, стороны которого 3 дм, 5 дм, 4 дм (размеры проставлены для учителя), и предлагает найти сумму длин всех сторон данного треугольника. 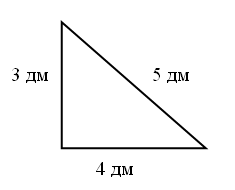 Учитель. Сколько сторон у данного треугольника? Что значит найти сумму длин всех его сторон? Дети. Это значит, нужно измерить каждую сторону, а затем сложить полученные числа. Учитель. Сколько отрезков надо измерить? Дети. Три отрезка. Учитель проводит измерения на доске, при этом обращая внимание на то, как следует прикладывать линейку при измерении каждой стороны треугольника. Учащиеся записывают результаты измерения: 5 дм, 4 дм, 3 дм. Учитель. Все ли стороны измерили? Назовите длину каждой стороны. В задаче требуется найти сумму длин всех сторон треугольника. Запись будет такая: 5 + 4 + 3 = 12 (дм). О т в е т: 12 дм. После этого учитель сообщает, что сумму длин сторон многоугольника называютпериметром. Обозначается периметр знаком Р. Аналогичную работу по измерению сторон многоугольников (задание № 1) и нахождению суммы длин всех сторон каждой фигуры дети выполняют с комментированием и записью решения на доске. Ф и з к у л ь т м и н у т к а Хомка, хомка, хомячок, Полосатенький бочок. Хомка раненько встаёт, Щёчки моет, Шейку трёт. Подметает хомка хатку И выходит на зарядку. Раз, два, три, четыре, пять, Хомка хочет сильным стать. Дети имитируют движения зверька. IV. Работа над пройденным материалом. 1. Работа над задачами. При необходимости задание № 5 можно разобрать у доски. Если дети уже хорошо усвоили решение такого вида задач, то задание выполняется самостоятельно. Задание № 6 выполняется учащимися самостоятельно с последующей проверкой. 2. Для самостоятельной работы можно предложить задания № 2 и № 3. V. Итоги урока. Учитель. Ребята, что нового узнали на уроке? Дети. На уроке мы познакомились с периметром и учились находить его у различных геометрических фигур. Учитель. Ребята, скажите мне ещё раз, что же такое периметр? Дети. Периметр – это сумма длин сторон многоугольника. Учитель. Что нужно знать, чтобы найти периметр? Дети. Надо знать длину каждой стороны многоугольника. Учитель. Что повторяли на уроке? Дети. Решали задачу и составляли к ней обратные задачи, решали также уравнения и примеры. Домашнее задание: с. 30, № 2, № 3. У р о к 25. ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО (с. 31) Цели: продолжать работу над задачами по нахождению периметра геометрических фигур, закреплять умение решать задачи и примеры. Ход урока I. Организационный момент. II. Устный счёт. 1. «Круговые примеры»: 35 – 20 42 – 10 9 + 40 82 – 60 15 – 6 22 + 13 32 + 50 49 – 7 |
