Основные требования к знаниям, умениям и навыкам учащихся
 Скачать 1.98 Mb. Скачать 1.98 Mb.
|
|
4. Для самостоятельной работы может быть предложено задание № 6, но перед выполнением с учащимися надо вспомнить, что 1 дм равняется 10 см. Учитель. Ребята, вспомните, сколько см в 1 дм? Дети. 10 см. Учитель. Верно. А теперь, пользуясь этим, сравните выражения самостоятельно, а потом проверим, что у вас получилось. V. Итоги урока. Учитель. Ребята, что мы повторяли сегодня на уроке? Дети. Сегодня на уроке мы вспомнили свойства сложения и применяли их при решении примеров; вспомнили также решение примеров на сложение и вычитание в пределах 100. Решали задачи и работали с геометрическими фигурами. Домашнее задание: с. 8, № 6. У р о к 5. ЕДИНИЦЫ ДЛИНЫ. МИЛЛИМЕТР (с. 9) Цели: познакомить учащихся с новой единицей длины – миллиметром, установить соотношение между миллиметром и сантиметром; повторить алгоритмы письменного сложения и вычитания в пределах 100; совершенствовать навык решения задач. Ход урока I. Организационный момент. II. Устный счёт. 1. На доске записаны примеры. Подберите такие числа, чтобы записи были верными: 45 – 10 < 45 – … 23 + 5 < 23 + … 18 + 40 > 18 + … 56 – 4 > 56 – … 2. Переведите: 80 см = … дм 5 дм = … см 9 дм 2 см = … см 67 см = … дм … см III. Работа над новым материалом. Работа над новым материалом на уроке зависит от уровня подготовленности детей и предполагает меньшую или большую степень их самостоятельности. В одном случае новый материал вводится в форме беседы о том, что миллиметр – это новая единица для определения длины отрезков. Показав на линейке отрезок в 1 мм, учитель вводит соотношение: 1 см равен 10 мм. Соответствующая запись выполняется на доске и в тетрадях. Полезно обратить внимание детей на то, что на линейке сантиметры обозначены длинными черточками, а миллиметры – короткими, но каждые пять миллиметров обозначены более длинной черточкой, что облегчает измерения. После этого учащиеся читают вводный текст в учебнике на с. 9 и под руководством учителя выполняют задания № 1 и № 2. № 1: измерьте длину каждого отрезка. 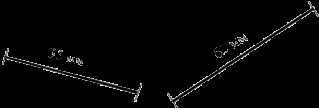 Дети измеряют и записывают результат в миллиметрах. № 2: начертите отрезки длиной 8 мм и 5 см 2 мм.  Если подготовка класса к данному моменту достаточно высокая, учитель может построить работу по-другому: на основе практической работы дети сами приходят к необходимости введения новой единицы длины, а затем подводятся к обобщению. Каждый ученик получает полоску бумаги и измеряет ее длину (длина ее выражается в сантиметрах и миллиметрах). Дети пользуются сантиметровой линейкой и убеждаются, что в целых сантиметрах измерить длину этой полоски нельзя. Учащиеся приходят к выводу, что нужна новая единицы длины, более мелкая, чем сантиметр. Используя учебник, дети узнают, что новая, более мелкая единица измерения называется миллиметром. После чтения в учебнике вводной статьи на с. 9 учащиеся приступают к выполнению заданий № 1 и № 2 под руководством учителя (см. выше). Ф и з к у л ь т м и н у т к а Руки в стороны – в полёт Отправляем самолёт. Правое крыло – вперёд, Левое крыло – вперёд. Раз, два, три, четыре – Полетел наш самолёт. (И. П. – стойка: ноги врозь, руки в стороны; 1 – поворот вправо; 2 – И. П.; 3 – поворот влево; 4 – И. П.) IV. Работа над пройденным материалом. 1. Для повторения алгоритмов письменного сложения и вычитания выполняется задание № 3. Полезно решить эти примеры у доски с подробным комментированием: 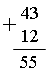 Ученик. Записываю десятки под десятками, единицы под единицами. Складываю единицы: 3 + 2, получится 5. Записываю под единицами. Складываю десятки: 4 + 1, получится 5. Записываю под десятками. Читаю ответ: 55. 2. Решение задач. Упражнение № 4 выполняется устно под руковод-ством учителя. Дети должны объяснить, что, вычислив разность 16 – 12, узнаем длину головы кита, а если к этой разности прибавить еще 16, то узнаем, какова длина всего кита. Задание № 5 можно предложить учащимся выполнить самостоятельно. После решения задачи осуществить проверку. 3. Для самостоятельной работы можно предложить выполнить задание № 6 и задание «Занимательные рамки» (на полях учебника). V. Итоги урока. Учитель. Ребята, что нового мы узнали сегодня на уроке? Над чем работали? Дети. Сегодня на уроке мы познакомились с новой единицей длины – миллиметром, измеряли и чертили отрезки в миллиметрах. Также вспомнили сложение и вычитание столбиком в пределах 100, решали задачи. Домашнее задание: с. 9, № 6. У р о к 6. УРАВНЕНИЕ (с. 10) Цели: дать понятие уравнения; научить правильно читать и решать уравнения методом подбора; закреплять письменные приемы сложения и вычитания; вспомнить сравнение единиц длины. Ход урока I. Организационный момент. II. Устный счёт. 1. Найдите и исправьте ошибки: 6 + 7 – 9 = 4 17 – 8 + 11 = 20 7 + 8 – 6 = 9 13 – 8 + 7 = 12 4 + 9 – 7 = 6 11 – 7 + 9 = 13 2. Арифметические ребусы – вставьте пропущенные цифры: 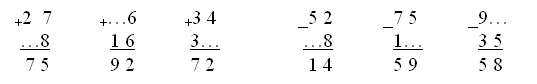 3. Решение простых задач на сложение и вычитание. Четыре-пять задач различных видов предлагаем в форме арифметического диктанта (учитель читает задачу, а дети записывают ее решение или только ответ). В автобусе ехало 17 человек. 5 человек вышли. Сколько человек осталось? Во дворе стояло 20 машин. Из них 8 легковых, а остальные грузовые. Сколько грузовых машин стояло во дворе? Вике 18 лет, а Карине 10 лет. На сколько лет Карина младше Вики? У Кости 13 красных шаров и столько же зеленых. Сколько всего шаров у Кости? Когда Дима подарил 5 календариков, у него осталось 18. Сколько календариков было у Димы? III. Работа над новым материалом. С целью подготовки введения нового материала решить с учащимися устно несколько примеров: 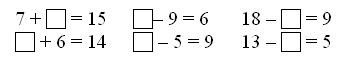 Учитель (поясняет). Неизвестные числа, которые надо найти, принято обозначать латинскими буквами; познакомимся еще с одной из них – буквой х. Далее учащиеся с учителем читают вводный текст в учебнике (с. 10). Учитель также знакомит детей с правильным чтением уравнения: х + 4 = 12 можно прочитать так: к неизвестному числу прибавить 4, получится 12. К какому числу надо прибавить 4, чтобы получилось 12? Дети. 8. Учитель. Первое слагаемое неизвестно, второе – 4, сумма равна 12. Решать уравнения на данном этапе следует устно методом подбора. Для закрепления выполнить задание № 1. Ф и з к у л ь т м и н у т к а А теперь насос включаем, Воду из реки качаем. Влево – раз, вправо – два, Потекла ручьём вода. Раз, два, три, четыре – Хорошо мы потрудились. (3 раза.) (И. П. – стойка: ноги врозь; 1 – наклон влево, правая рука скользит вверх вдоль туловища (до подмышечной впадины); 2 – И. П.; 3 – наклон вправо, движение вверх левой рукой; 4 – И. П.) IV. Работа над пройденным материалом. 1. Выполняя работу по сравнению единиц длины (задание № 3), надо добиться от учащихся не только постановки знака, но и объяснения, почему такой знак поставлен. Ученик. 1 см 6 мм … 16 мм В 1 см содержится 10 мм. Значит, в левой части 1 см = 10 мм да ещё 6 мм. Всего получается 16 мм. А в правой части тоже 16 мм. Значит, ставим знак =. 1 см 6 мм = 16 мм. Аналогично рассуждают дети и при решении других примеров. 2. Для самостоятельной работы можно использовать примеры задания № 2. V. Итоги урока. Учитель. Ребята, что нового мы узнали сегодня на уроке? Над чем работали? Дети. Сегодня на уроке мы познакомились с уравнениями, учились читать, записывать их и решать способом подбора. На уроке также решали задачи, арифметические ребусы, сравнивали единицы длины. Домашнее задание: с. 10, № 2. У р о к 7. ПОВТОРЕНИЕ СВЯЗИ МЕЖДУ КОМПОНЕНТАМИ И РЕЗУЛЬТАТОМ СЛОЖЕНИЯ (с. 11) Цели: повторить связь между компонентами и результатом сложения; научить решать уравнения, опираясь на эту связь; закреплять навык решения составных задач. Ход урока I. Организационный момент. II. Устный счёт. 1. Поставьте нужные знаки «+», «–» так, чтобы равенства остались верными: (40 … 25) … 5 = 20 50 … (43 … 10) = 83 (90 … 35) … 20 = 80 (16 … 3) … 7 = 20 2. Продолжите ряды чисел: 26, 37, 48, …, …, …, … . 88, 87, 85, 82, 78, …, …, …, … . III. Повторение пройденного материала. 1. Повторение связи между суммой и слагаемыми можно провести на основе сравнения троек взаимосвязанных примеров (задание № 1). 10 + 7 = 17 17 – 7 = 10 17 – 10 = 7 После решения примера на сложение дети должны прочесть запись, используя термины «слагаемое» и «сумма». Ученик. Запись 10 + 7 = 17 читается так: 10 – первое слагаемое, 7 – второе слагаемое, 17 – сумма. Учащиеся, сравнивая второй пример с первым, объясняют, что из суммы (17) вычли второе слагаемое (7), и устанавливают, что при этом получили первое слагаемое (10). Так же сравнивают третий пример с первым и устанавливают, что если из суммы (17) вычесть первое слагаемое (10), то получится второе слагаемое (7). Аналогичные объяснения должны быть даны при рассмотрении следующих троек примеров. Затем дети читают вывод, помещенный в учебнике в рамке. Если из суммы двух слагаемых вычесть одно из них, то получится другое слагаемое. Учитель. Как можно использовать этот вывод для проверки сложения? Ученики. Для проверки сложения можно из полученной суммы вычесть одно из слагаемых. Если получится другое слагаемое, значит, пример решен верно. 2. Для закрепления знания связи между суммой и слагаемыми дети заполняют таблицу (задание № 2), записанную предварительно учителем на доске.
Пояснения будут такими: «Сумма 20, второе слагаемое 5. Мы знаем, что если из суммы вычесть второе слагаемое, то получится первое слагаемое: 20 – 5 = 15, значит, первое слагаемое равно 15». 3. Используя вывод о связи между суммой и слагаемыми, учащиеся под руководством учителя решают с комментированием уравнения (задания № 3 и № 4). № 3: х + 6 = 38 х = 38 – 6 х = 32 32 + 6 = 38 38 = 38 Рассуждения могут быть следующими: «Первое слагаемое неизвестно, второе слагаемое 6, сумма равна 38. Чтобы найти первое слагаемое, надо из суммы вычесть второе слагаемое. Значит, 38 – 6 = 32, х = 32. Выполняем проверку. Вместо х подставляем число 32. Складываем: 32 + 6. Получаем 38. Значит, уравнение решили верно». № 4: х + 18 = 42 64 + х = 82 х = 42 – 18 х = 82 – 64 х = 24 х = 18 24 + 18 = 42 64 + 18 = 82 42 = 42 82 = 82 Комментарии такие же, как и при выполнении № 3. Ф и з к у л ь т м и н у т к а Раз, два – выше голова, Три, четыре – руки шире, Пять, шесть – тихо сесть, Семь, восемь – лень отбросим. Раз – согнуться, разогнуться, Два – нагнуться, потянуться, Три – в ладоши три хлопка, Головою три кивка. На четыре – руки шире, Пять, шесть – тихо сесть, Семь, восемь – лень отбросим. IV. Решение задач. Задание № 6 выполняется под руководством учителя. После повторения и краткой записи условия дети должны объяснить, что, вычислив сумму 20 + 5, узнаем, сколько килограммов картофеля собрали со второй грядки, а если к этой сумме прибавить еще 20, то узнаем, сколько всего картофеля собрали с этих двух грядок.
1) 20 + 5 = 25 (кг) – со 2-й грядки 2) 20 + 25 = 45 (кг) О т в е т: 45 кг картофеля всего. Задание № 7 можно предложить учащимся решить самостоятельно, а затем проверить решение. V. Итоги урока. Учитель. Ребята, что мы повторяли сегодня на уроке? Дети. Мы повторяли, какая связь существует между компонентами и результатом сложения. Учитель. Какую же связь мы установили? Дети. Мы установили, что если из суммы вычесть одно слагаемое, то получится другое слагаемое. Учитель. Где использовали это правило на уроке? Дети. Это правило мы применяли при проверке сложения и при решении уравнений. Учитель. Что ещё мы повторяли сегодня на уроке? Дети. А ещё на уроке мы повторили решение задач и примеров. Домашнее задание: с. 11, № 7. У р о к 8. ПОВТОРЕНИЕ СВЯЗИ МЕЖДУ КОМПОНЕНТАМИ И РЕЗУЛЬТАТОМ ВЫЧИТАНИЯ (с. 12) Цели: повторить связь между компонентами и результатом вычитания; использовать полученные выводы для проверки вычитания; закреплять умение находить значение выражения с переменной. Ход урока I. Организационный момент. II. Устный счёт. 1. Игра «Составление поезда из примеров». Учитель выставляет вразброс картинки с записанными на них примерами: 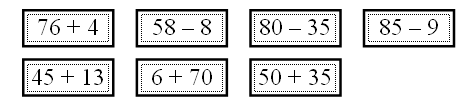 Дети должны составить поезд из вагончиков (карточек с примерами) так, чтобы пример на следующем вагончике начинался с числа, совпадающего с ответом примера на предыдущем вагончике.  2. Составьте и решите тройки примеров: … + 9 = 17 6 + … = 14 … + 5 = 13 17 – 9 = ………….. …………… ………….. ………….. …………… III. Объяснение нового материала. 1. Подготовка к восприятию и усвоению выводов, характеризующих связь между уменьшаемым, вычитаемым и разностью, ведется аналогично тому, как это делалось на предыдущем уроке (задание № 1). Затем дети читают выводы, помещенные в учебнике в рамке. Если к разности прибавить вычитаемое, то получится уменьшаемое. Если из уменьшаемого вычесть разность, то получится вычитаемое. 2. После разбора выводов учащиеся приступают к выполнению задания № 2 с комментированием у доски: 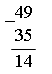 Ученик. Записываю десятки под десятками, единицы под единицами. Вычитаю единицы: 9 – 5, получится 4. Записываю под единицами. Вычитаю десятки: 4 – 3, получится 1. Записываю под десятками. Читаю ответ: 14. Учитель. Как можно использовать эти правила для проверки вычитания? Дети. Для проверки вычитания нужно к полученной разности прибавить вычитаемое. Если получится уменьшаемое, значит, пример решен верно. Проверка примера: 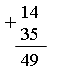 |
