Основные требования к знаниям, умениям и навыкам учащихся
 Скачать 1.98 Mb. Скачать 1.98 Mb.
|
|
2. Решите цепочки примеров:  III. Повторение пройденного материала. 1. Решение задач. Задание № 1 (1, 2) учащиеся решают самостоятельно. После решения учащиеся делают вывод, что в первой задаче первым действием выполнялось деление, а во второй задаче первым действием – вычитание. Вторые действия одинаковые – сложение. После этого разобрать задание № 2 (1, 2) устно. Дети по выражениям составляют задачи, потом сравнивают и находят сходства и отличия. Задание № 3 учащиеся выполняют самостоятельно (с последующей проверкой). 2. Для самостоятельной работы на уроке можно предложить задания № 4, № 5, № 6. Задание № 7 учитель разбирает вместе с детьми. Это задание подготавливает учащихся к введению понятия площади. Учитель. Посчитайте количество клеточек в каждой фигуре. Самый простой способ – это когда дети просто пересчитывают количество клеток и выясняют, что в желтой фигуре их больше, чем в синей. Затем учитель просит: – Подумайте, как еще можно посчитать количество клеток. Ученики. Посчитаем сначала количество клеток в одном длинном ряду у желтой фигуры. Их там 9, а таких рядов 2, значит, 9 · 2, да еще потом надо прибавить 3 клетки. Получается: 9 · 2 + 3 = 21. У синей фигуры 2 ряда по 7 клеток да еще 5, значит, 7 · 2 + 5 = 19. IV. Итоги урока. Учитель. Ребята, что закрепляли мы сегодня на уроке? Дети. На уроке мы закрепляли решение задач, примеров, уравнений, писали арифметический диктант. Домашнее задание: с. 66, № 4, № 5, № 6. У р о к 54. ТАБЛИЦА УМНОЖЕНИЯ И ДЕЛЕНИЯ С ЧИСЛОМ 7 (с. 67) Цели: составить с учащимися и начать разучивать таблицу умножения и деления с числом 7; использовать полученные знания при решении задач и примеров; продолжить работу по закреплению вычислительных навыков. Ход урока I. Организационный момент. II. Устный счёт. 1. Для устного выполнения предложить задание «Вычислить устно, записывая только результаты (запись на доске)»: 36 + 54 : 9 6 · 7 + 8 32 : 8 35 : 5 (36 + 54) : 9 8 + 6 · 7 48 : 6 36 : 6 2. Вставьте пропущенные числа: 6 · … = 18 4 · … = 20 7 · … = 14 … · 2 = 10 6 · … = 12 … · 3 = 15 … · 5 = 15 … · 3 = 9 4 · … = 12 3. Даны числа (запись на доске): 20, 21, 22, 23, 24, 25. Назовите чётные числа. Составьте и вычислите различные суммы, слагаемые которых состоят из 2 чётных данных чисел. Составьте и вычислите различные суммы, слагаемые которых состоят из двух нечётных указанных чисел. III. Работа над новым материалом. Таблицы умножения и деления с числом 7 можно ввести так же, как таблицы с другими числами (см. урок № 37). Учителю следует помнить, что надо повторить и другие случаи умножения с числом 7, рассмотренные в других таблицах. С целью закрепления изученного выполнить задания № 1, № 5 и задание «Какое число лишнее?» (на полях учебника). Ф и з к у л ь т м и н у т к а Солнце глянуло в кроватку… Раз, два, три, четыре, пять. Все мы делаем зарядку, Надо нам присесть и встать. Руки вытянуть пошире, Раз, два, три, четыре, пять. Наклониться – три, четыре, И на месте поскакать. На носок, потом на пятку. Все мы делаем зарядку. IV. Работа над пройденным материалом. 1. Решение задач. Задание № 2 записать кратко под руководством учителя, после чего дети решают его самостоятельно. Учитель оказывает помощь некоторым детям индивидуально. Грузовых – 15 м. Легковых – ? на 25 м. б. Мотоциклов – ? в 5 раз м. Перед выполнением задания № 4 учащиеся ставят вопрос к задаче: «Сколько литров бензина осталось?», а после этого решают задачу самостоятельно с последующей проверкой. 2. Для самостоятельной работы предложить выполнить задания № 3 и № 6. Задание № 7 дети выполняют вместе с учителем. Оно подготавливает детей к введению новой величины «Площадь фигур». V. Итоги урока. Учитель. Ребята, что нового узнали мы сегодня на уроке? Дети. Сегодня на уроке мы составляли таблицу умножения и деления с числом 7. Учитель. Что ещё повторяли и закрепляли на уроке? Дети. Повторяли таблицу умножения и деления, вспоминали, какие числа называются чётными, а какие нечётными, решали задачи. Домашнее задание: с. 67, № 3, № 6. У р о к 55. ПЛОЩАДЬ ФИГУР (с. 68–69) Цели: познакомить учащихся с новой величиной – площадью; дать представление о площади фигур; научить сравнивать площади фигур путем их наложения друг на друга и путем разбиения их на квадраты; закреплять табличные случаи умножения и деления. Ход урока I. Организационный момент. II. Устный счёт. 1. Назовите числа от 7 до 63, которые делятся на 7 без остатка. Назовите числа от 24 до 54, которые делятся на 6 без остатка. 2. Вычислите и найдите лишнее выражение: 49 : 7 = 70 : 10 = 28 : 4 = 56 : 8 = 42 : 6 = 63 : 9 = 35 : 5 = 54 : 6 = 3. Заполните пропуски: 19 = … · 3 + … 28 = … · 6 + … … · 4 – … = 20 8 · … – … = 37 III. Работа над новым материалом. Ознакомление с площадью можно провести так. Учитель. Посмотрите на фигуры, прикрепленные к доске: 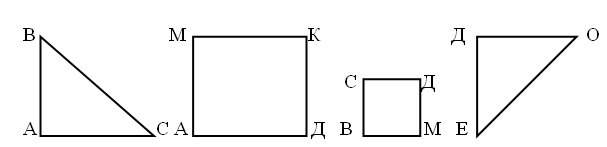 Скажите, какая из них занимает больше всего места на доске? Дети. Квадрат АМКД занимает места больше всех фигур. Учитель. В этом случае говорят, что площадь квадрата больше, чем площадь каждого треугольника и квадрата СДМВ. Сравните площадь треугольника АВС и квадрата АМКД. Дети. Площадь треугольника меньше, чем площадь квадрата. Учитель. Посмотрите, я сравню эти фигуры наложением: треугольник занимает только часть квадрата, значит, действительно площадь его меньше площади квадрата. Сравните на глаз площадь треугольника АВС и площадь треугольника ДОЕ. Дети. У них площади одинаковые, они занимают одинаковое место на доске, хотя расположены по-разному. Учитель. Проверьте наложением. Аналогично сравниваются по площади другие фигуры, а также предметы окружающей обстановки. Однако не всегда так легко установить, какая из двух фигур имеет большую (меньшую) площадь или они одинаковы по площади. Чтобы показать это учащимся, можно предложить им сравнить вырезанные из бумаги прямоугольник и квадрат, незначительно отличающиеся по площади, например: размер квадрата 4 х 4 дм, а прямоугольника 5 х 3 дм, при этом фигуры с обратной стороны разбиты на квадратные дециметры. Сначала учащиеся пытаются сравнить эти фигуры на глаз, а также путем наложения. Однако оба способа не помогают детям решить вопрос убедительно. Выслушав различные предположения, учитель поворачивает фигуры той стороной, на которой сделана разбивка на квадраты, и предлагает сосчитать, сколько одинаковых квадратов содержит каждая фигура. На этой основе дети устанавливают, площадь какой фигуры больше, а какой – меньше. Аналогичные упражнения на сравнение площади фигур, составленных из одинаковых квадратов, выполняются по учебнику, а также по чертежам, данным на доске. Дети убеждаются в том, что если фигуры состоят из одинаковых квадратов, то площадь той фигуры больше (меньше), которая содержит больше (меньше) квадратов. Полезно на этом же уроке рассмотреть такой случай, когда разные по форме фигуры имеют одинаковую площадь, так как содержат одинаковое число квадратов (например, квадрат – 16 кв. ед. и прямоугольник – 16 кв. ед.). После этого учащиеся читают вводную статью в учебнике на с. 68. Для закрепления выполнить задание № 1 на с. 69. Ф и з к у л ь т м и н у т к а Хомка, хомка, хомячок, Полосатенький бочок. Хомка раненько встаёт, Щёчки моет, Шейку трёт. Подметает хомка хатку И выходит на зарядку. Раз, два, три, четыре, пять, Хомка хочет сильным стать. Дети имитируют движения зверька. IV. Работа над пройденным материалом. 1. Решение задач. Учитель вместе с учащимися записывает кратко условие задачи № 4: Было – 8 м Отпилили – 2 м Осталось – ? В ходе беседы выясняется, что сразу ответить на главный вопрос нельзя, так как неизвестно, сколько метров осталось. Но это можно найти вычитанием. Затем дети вспоминают, как узнать, во сколько раз одно число больше или меньше другого. После этого учащиеся записывают решение и ответ самостоятельно. 2. Для самостоятельной работы предложить задания № 2 и № 5. V. Итоги урока. Учитель. Ребята, что нового мы сегодня узнали на уроке? Дети. Сегодня на уроке мы узнали новую величину – площадь. Мы также сравнивали площади фигур. Учитель. А как можно сравнить площади фигур? Дети. Можно наложить одну фигуру на другую, а можно разбить каждую из предложенных фигур на квадраты, посчитать количество квадратов в каждой фигуре и сравнить их. Учитель. Что мы повторяли сегодня на уроке? Дети: Мы повторяли табличные случаи умножения и деления, а также решение задач. Учитель. Какое задание на уроке понравилось вам больше всего? Какое – меньше? Домашнее задание: с. 69, № 2, № 5. У р о к 56. ЕДИНИЦА ПЛОЩАДИ. КВАДРАТНЫЙ САНТИМЕТР (с. 70–71) Цели: познакомить учащихся с единицей площади – квадратным сантиметром; дать представление о квадратном сантиметре; продолжать закреплять навыки решения задач и примеров. Ход урока I. Организационный момент. II. Устный счёт. 1. Каждое из чисел 72, 56, 48, 64 уменьшите на 40, а результат уменьшите в 4 раза. Каждое из чисел 12, 16, 20, 24 уменьшите в 4 раза, а результат увеличьте в 7 раз. 2. Найдите значение выражений: 100 – 6 · 9 = 6 · 4 : 3 + 24 = 6 · 7 + 28 = 48 : (16 : 2) · 5 = 4 · 8 – 27 : 3 = 90 – (3 · 6 + 30) = 3. Посчитайте, сколько треугольников на чертеже: 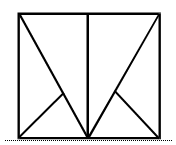 III. Работа над новым материалом. Урок можно начать с выполнения такого задания: учитель показывает прямоугольник, разбитый с одной стороны на клеточки, и просит найти площадь данной фигуры. Учащиеся считают и говорят ответ (например, 12 клеток). Тогда учитель переворачивает этот же прямоугольник другой стороной, где он тоже разбит на клетки, но более крупные, и просит найти площадь этой же фигуры. Учащиеся считают и говорят ответ (например, 6). После этого учитель спрашивает: – Мы измеряли площадь одной и той же фигуры, а ответы получили разные. Почему? Дети. Потому что в первом случае клетка была мелкая, а во втором – крупнее. Учитель. Чтобы не получать разные ответы при измерении площади одной фигуры, есть специальная единица измерения площади – квадратный сантиметр. Квадратный сантиметр – это площадь квадрата со стороной 1 см. Учитель показывает учащимся модель квадратного сантиметра, и дети вычерчивают в тетрадях квадратный сантиметр. Учитель также сообщает: – Слова «квадратный сантиметр» при числах сокращенно записывают так: 1 см2. Далее учащиеся еще раз читают вводную статью в учебнике на с. 70. Для закрепления выполнить задание № 1. Учитель может также предложить аналогичное задание по своим фигурам. Ф и з к у л ь т м и н у т к а А теперь насос включаем, Воду из реки качаем. Влево – раз, вправо – два, Потекла ручьём вода. Раз, два, три, четыре – Хорошо мы потрудились. (3 раза.) IV. Работа над пройденным материалом. 1. Решение задач. Условие задач № 4 и № 5 учащиеся записывают в виде таблицы и решают самостоятельно с последующей проверкой. Задачу № 7 разобрать с комментированием у доски. Даны выражения, надо составить и решить по ним задачи: 3 · 8 + 6; 5 · 4 – 15. Дети могут предложить такого вида задачи: 1) Таня пришила к 8 платьям по 3 пуговицы, и у неё ещё осталось 6 пуговиц. Сколько всего пуговиц было у Тани? 2) В 4 вазах стояло по 5 цветов. 15 цветов взяли. Сколько цветов осталось в вазах? 2. Для самостоятельной работы предложить задание № 8. V. Итоги урока. Учитель. Ребята, что нового вы узнали сегодня на уроке? Дети. Сегодня мы познакомились с единицей площади – квадратным сантиметром, измеряли фигуры квадратными сантиметрами; узнали, как правильно записывать квадратный сантиметр. Учитель. А что мы повторяли сегодня на уроке? Дети. Продолжали учиться решать примеры и задачи. Домашнее задание: с. 71, № 8. У р о к 57. ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА (с. 72–73) Цели: научить вычислять площадь прямоугольника, зная длину его сторон; продолжить работу над задачами на нахождение четвертого пропорционального; отрабатывать вычислительные навыки. Ход урока I. Организационный момент. II. Устный счёт. 1. Вычислите. Найдите лишнее выражение: 48 : 8 = 42 : 7 = 36 : 6 = 56 : 7 = 60 : 10 = 30 : 5 = 54 : 9 = 2. Игра «Цепочка». 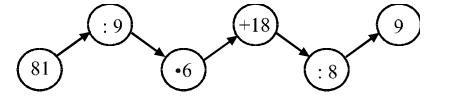 3. Игра «Молчанка». 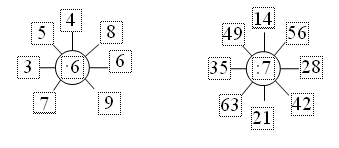 III. Работа над новым материалом. Работу над новым материалом можно начать с выполнения практической работы. Учитель просит начертить учащихся в тетради прямоугольник со сторонами 7 см и 3 см и разбить его на квадратные сантиметры. Учитель. Все квадратные сантиметры составляют несколько рядов. Сколько этих рядов? Дети. 3 ряда. Учитель. А сколько в каждом ряду квадратных сантиметров? Дети. 7 квадратных сантиметров. Учитель. Верно. Их столько, сколько сантиметров в длине прямоугольника. А рядов получилось столько, сколько сантиметров в ширине прямоугольника. Кто из вас догадался, как найти площадь прямоугольника? Дети. Надо 7 умножить на 3. Записывают на доске и в тетради решение и ответ (учитель также знакомит со знаком обозначения площади – S). 7 · 3 = 21 (см2) О т в е т: S = 21 см2. После этого учитель сообщает: – Площадь того же прямоугольника можно вычислить и иначе. Все квадратные сантиметры составляют несколько вертикальных столбцов. В каждом столбце по 3 квадратных сантиметра (столько, сколько сантиметров в ширине прямоугольника). Столбцов получилось столько, сколько сантиметров в длине прямоугольника. Как же можно найти площадь этого прямоугольника? Дети. Нужно 3 умножить на 7. Записывают решение и ответ. 3 · 7 = 21 (см2) О т в е т: S = 21 см2. Учитель продолжает беседу: – Ребята, посмотрите еще раз внимательно на решение задачи и скажите общий вывод: как найти площадь прямоугольника? Учащиеся. Для нахождения площади прямоугольника достаточно измерить его длину и ширину в сантиметрах и полученные числа перемножить. Площадь прямоугольника будет выражена в квадратных сантиметрах. После этого учащиеся читают еще раз вводную статью на с. 72 и правило внизу. Для закрепления изученного учащиеся под руководством учителя выполняют задания № 1, № 2, № 3 и № 4. После решения задачи № 4 учащиеся приходят к выводу, что площадь квадрата находится так же, как и площадь прямоугольника, достаточно знать только длину его стороны. Ф и з к у л ь т м и н у т к а Раз, два – выше голова, Три, четыре – руки шире, Пять, шесть – тихо сесть, Семь, восемь – лень отбросим. Раз – согнуться, разогнуться, Два – нагнуться, потянуться, Три – в ладоши три хлопка, Головою три кивка. На четыре – руки шире, Пять, шесть – тихо сесть, Семь, восемь – лень отбросим. IV. Работа над пройденным материалом. Для самостоятельной работы можно предложить задания № 5, № 6, № 7, № 8. |
