Основные требования к знаниям, умениям и навыкам учащихся
 Скачать 1.98 Mb. Скачать 1.98 Mb.
|
|
V. Итоги урока. Учитель. Ребята, что нового вы сегодня узнали на уроке? Дети. На уроке мы узнали, как можно вычислить площадь прямоугольника. Учитель. Как же можно найти площадь прямоугольника? Дети. Чтобы найти площадь прямоугольника, надо длину умножить на ширину. Домашнее задание: с. 73, № 7, № 8. У р о к 58. ТАБЛИЦЫ УМНОЖЕНИЯ И ДЕЛЕНИЯ С ЧИСЛОМ 8 (с. 74) Цели: составить и начать разучивать таблицу умножения и деления с числом 8; продолжать работу над задачами на нахождение площади и периметра прямоугольника; закреплять вычислительные навыки. Ход урока I. Организационный момент. II. Устный счёт. 1. В целях закрепления навыков сложения в пределах 100 в устные упражнения включить «Лабиринты». 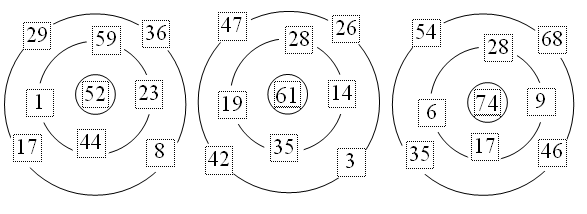 2. Проверьте, верны ли неравенства. Исправьте ошибки. 15 : 3 < 5 2 · 5 < 5 · 2 7 + 7 + 7 + 7 > 4 · 3 (78 – 8) : 2 > 10 8 : 2 > 6 : 3 (15 + 5) · 2 < 15 + 5 4 м < 38 дм 4 дм 5 см > 44 см III. Работа над новым материалом. В качестве подготовки к составлению таблицы умножения числа 8 необходимо непосредственно перед началом работы над новым материалом повторить известные уже детям случаи умножения на 8 (2 · 8, 3 · 8, 4 · 8, 5 · 8, 6 · 8, 7 · 8). Эти примеры полезно заранее записать на доске, чтобы детям оставалось записать только ответы. При решении полезно 2–3 раза спросить, как можно вычислить результат, если он забыт. Дети могут при этом предложить разнообразные способы. Например: 2 · 8 = 16, так как 8 + 8 = 16, 4 · 8 = 32, так как если взять 5 раз по 4, получится 20, да еще 3 раза по 4, получится 12, а 20 + 12 = 32 и т. п. Следует отметить, что хотя все эти случаи умножения на 8 дети уже учили, они запоминаются труднее, чем другие. Вместе с тем, они основа для составления таблицы умножения числа 8, в которой новыми для детей будут только примеры: 8 · 8, 8 · 9. Полезно поэтому, чтобы на доске была составлена вся таблица умножения числа 8, а последние два примера в ней могут быть выделены цветом или подчеркнуты. При решении знакомых примеров дети будут опираться на использование приема перестановки множителей, при вычислении произведения 8 · 8 могут воспользоваться приемом набора слагаемых группами (например: 8 · 4 = 32 и еще 8 · 4 = 32, 32 + 32 = 64 или 8 · 5 = 40, да еще 8 · 3 = 24, 40 + 24 = 64). Они могут так же, как это уже неоднократно делалось, найти результат, опираясь на ответ предыдущего примера в таблице (8 · 7 = 56, 56 + 8 = 64). Этим приемом они могут воспользоваться и вычисляя произведение 8 · 9. Затем, как обычно, на основе примера на умножение составляется и записывается пример, полученный из него перестановкой множителей, и соответствующие примеры на деление. После того как таблица составлена и записана в тетради, можно обратиться к учебнику. Пусть дети сами рассмотрят рисунок, данный вверху на с. 74, и воспроизведут по нему только что составленную таблицу (учитель задает примеры из таблицы подряд, ученики один за другим, используя рисунок, говорят ответы). Для закрепления выполнить задание № 2. Ф и з к у л ь т м и н у т к а Солнце глянуло в кроватку… Раз, два, три, четыре, пять. Все мы делаем зарядку, Надо нам присесть и встать. Руки вытянуть пошире, Раз, два, три, четыре, пять. Наклониться – три, четыре, И на месте поскакать. На носок, потом на пятку. Все мы делаем зарядку. IV. Работа над пройденным материалом. 1. Решение задач. Под руководством учителя можно выполнить задание № 4 (1, 2). По ходу чтения задачи, при повторении детьми ее условия и вопроса, записываем их кратко на доске: Лук – 24 кг Чеснок – ? в 4 раза м. Морковь – ? в 5 раз б. Повторив задачу по этой краткой записи, ученики намечают кратко план решения: сначала надо узнать, сколько собрали чеснока, а потом – сколько собрали моркови. Если учитель не уверен, что все дети справятся после этого с решением самостоятельно, можно задать уточняющий контрольный вопрос: «Каким действием вы будете узнавать, сколько собрали чеснока? Почему?». Дети самостоятельно пишут решение, которое необходимо проверить в классе. При этом выбор каждого действия должен обосновываться. Затем учитель предлагает детям составить задачу, похожую на только что решенную по выражению, предложенному в задании № 4 (2). Прослушиваются 2 –3 задачи, составленные учащимися, и каждый решает придуманную им задачу, записывая ответ. Дано выражение: (15 : 3) · 2. Дети могут составить задачу, подобную следующей: «На 3 листах 15 переводных картинок. Сколько переводных картинок на 2 таких листах?». Перед выполнением задания № 5 учащиеся должны вспомнить правила нахождения периметра и площади прямоугольника. После этого самостоятельно записывают решение и ответ задачи. 2. Для самостоятельной работы на уроке предложить задания № 1, № 3, № 6. V. Итоги урока. Учитель. Ребята, что нового мы сегодня узнали на уроке? Дети. Сегодня мы составляли таблицу умножения и деления с числом 8. Учитель. Что повторяли на уроке? Дети. Мы вспоминали решение задач, примеров, уравнений, находили площадь и периметр прямоугольника. Домашнее задание: с. 74, № 1, № 3, № 6. У р о к 59. ЗАКРЕПЛЕНИЕ ЗНАНИЯ ТАБЛИЦЫ УМНОЖЕНИЯ И РЕШЕНИЕ ЗАДАЧ (с. 75) Цели: продолжать работу по закреплению табличных случаев умножения и деления; закреплять умение решать и анализировать задачи. Ход урока I. Организационный момент. II. Устный счёт. 1. Заполните таблицу:
При заполнении данной таблицы учащиеся должны отметить, что делимое постоянно, а делитель увеличивается. После того как дети найдут значения частного, они делают вывод, что при увеличении делителя частное уменьшается. 2. Поставьте нужные знаки: +, –, ·, :. 26 * 6 * 7 = 13 8 * 9 * 2 = 70 7 * 9 * 2 = 18 9 * 9 * 2 = 20 2 * 2 * 4 = 0 9 * 2 * 2 = 16 III. Повторение пройденного материала. 1. Решение задач. Задание № 1 (1 и 2) учащиеся выполняют под руководством учителя. Сначала читают данное условие задачи, затем рассматривают выражение. После этого анализируют, что запись 10 · 5 показывает, сколько денег у Сережи, а прибавив еще 50, получим, сколько всего денег у мальчиков. Значит, вопрос задачи будет звучать так: «Сколько всего денег у мальчиков?». Аналогично разбирается задание № 1 (2). После этого учащиеся самостоятельно записывают условие задачи в тетрадь, а также решение и ответ. Задание № 4 (1 и 2) дети решают с комментированием. При разборе можно вести рассуждения, отправляясь от данных («8 наборов стоят 80 р. Что можно узнать по этим данным?»), а можно от вопроса («Нужно узнать, сколько стоят 5 таких наборов. Что для этого нужно знать? Знаем ли мы это?»). Как в том, так и в другом случае разбор должен быть завершен составлением краткого плана решения: «Сначала узнаем, сколько стоит 1 набор бумаги, а потом – сколько стоят 5 таких наборов». Выполняют решение дети сами. Аналогично разбирается задание № 4 (2), а после этого сравниваются решения задач. Учащиеся находят сходства и отличия. 2. Для самостоятельной работы можно рекомендовать решение примеров № 2. Ф и з к у л ь т м и н у т к а А теперь насос включаем, Воду из реки качаем. Влево – раз, вправо – два, Потекла ручьём вода. Раз, два, три, четыре – Хорошо мы потрудились. (3 раза.) IV. Итоги урока. Учитель. Ребята, что закрепляли мы сегодня на уроке? Дети. На уроке мы закрепляли изученные случаи умножения и деления, решали и сравнивали решение задач. Домашнее задание: с. 75, № 2. У р о к 60. ЗАКРЕПЛЕНИЕ ЗНАНИЯ ИЗУЧЕННЫХ ТАБЛИЦ УМНОЖЕНИЯ И ДЕЛЕНИЯ (с. 76) Цели: закреплять табличные случаи умножения и деления, а также навыки решения задач. Ход урока I. Организационный момент. II. Устный счёт. 1. В целях закрепления табличных случаев умножения и деления проводим арифметический диктант: 5 · 6 42 : 6 8 · 5 54 : 9 32 : 8 21 : 3 56 : 7 24 : 8 28 : 4 6 · 6 7 ·2 8 ·8 2. Найдите периметр и площадь прямоугольников (чертежи на доске): 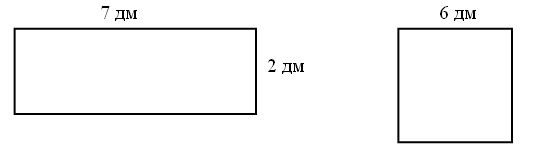 III. Повторение пройденного материала. 1. Решение задач. Задание № 2 содержит 2 вопроса, поэтому учащиеся решают его как две самостоятельные задачи. Записывают условие кратко в виде таблицы:
Далее решение и ответ записывают самостоятельно. После решения второй задачи учитель проводит проверку. Задание № 4 учитель разбирает вместе с детьми. После чтения условия задачи учитель на доске, а учащиеся у себя в тетради делают чертеж, заносят все данные и смотрят, что по чертежу неизвестно.  Затем дети ставят вопрос: «Сколько метров дорожки расчистил папа?». Анализируя задачу, дети должны увидеть, что вся дорожка разбита как бы на 3 части, 2 части из них известны, надо найти третью часть. Учащиеся составляют план решения задачи: сначала надо найти длину 2 частей, то есть сколько метров расчистили Миша и Ира. Затем из всей длины дорожки вычесть найденное число. Дети записывают самостоятельно решение и ответ. При разборе задачи № 3 учитель просит детей вспомнить, сколько дней в одной неделе. После этого вместе с учащимися записывают условие: На даче – 10 д. В доме отдыха – 2 нед. по 7 д. Далее дети записывают самостоятельно решение и ответ. Учитель оказывает индивидуальную помощь некоторым учащимся, кто затрудняется записать решение задачи. 2. Для самостоятельной работы предложить примеры № 1. 3. Если останется время на уроке – выполнить задание № 5 и задание «Задача на смекалку» (внизу страницы учебника). Ф и з к у л ь т м и н у т к а Хомка, хомка, хомячок, Полосатенький бочок. Хомка раненько встаёт, Щёчки моет, Шейку трёт. Подметает хомка хатку И выходит на зарядку. Раз, два, три, четыре, пять, Хомка хочет сильным стать. Дети имитируют движения зверька. IV. Итоги урока. Учитель. Ребята, что закрепляли мы сегодня на уроке? Дети. На уроке мы писали арифметический диктант по изученной таблице умножения, находили площадь и периметр прямоугольников, решали задачи и примеры. Домашнее задание: с. 76, № 1. У р о к 61. КОНТРОЛЬНАЯ РАБОТА I вариант 1. В саду росло 4 гладиолуса, а лилий – на 8 больше. Во сколько раз меньше росло в саду гладиолусов, чем лилий? 2. Найдите значение выражений: 47 + 5 · 3 – 18 = (36 : 6 + 3) · 2 = 3. Найдите площадь и периметр прямоугольника со сторонами 7 см и 5 см. 4. Решите уравнения: х · 4 = 36 х : 6 = 9 5. Сравните: 3 дм 4 см … 4 дм 3 см 63 см … 7 дм 40 см … 4 дм 2 см … 9 мм 6. Каждые понедельник, среду и четверг папа покупает по одной газете. Сколько газет папа купит за 8 недель? II вариант 1. Хозяйка купила 3 кг яблок, а груш – на 6 кг больше. Во сколько раз больше купила хозяйка груш, чем яблок? 2. Найдите значение выражений: (3 · 8 – 20) · 6 = 38 + 3 · 4 – 17 = 3. Длина прямоугольника 8 дм, а ширина 6 дм. Найдите его площадь и периметр. 4. Сравните: 7 · х = 28 48 : х = 6 5. Сравните: 6 мм … 4 см 8 дм 2 см … 2 дм 8 см 70 см … 7 дм 34 см … 4 дм 6. Каждые вторник, четверг и субботу Алёша смотрит по одному новому мультфильму. Сколько новых мультфильмов Алёша посмотрит за 6 недель? У р о к 62. РАБОТА НАД ОШИБКАМИ. ЗАКРЕПЛЕНИЕ ПРОЙДЕННОГО На этом уроке учитель даёт анализ проведённой контрольной работы, проводит с учащимися работу над ошибками в тех заданиях, где было допущено их больше всего, подбирает похожие задания, чтобы отработать необходимые навыки и умения. У р о к 63. ТАБЛИЦЫ УМНОЖЕНИЯ И ДЕЛЕНИЯ С ЧИСЛОМ 9 (с. 77) Цели: составить и начать разучивать таблицу умножения и деления с числом 9; использовать полученные знания для решения задач и примеров; повторить соотношения между единицами длины. Ход урока I. Организационный момент. II. Устный счёт. 1. Для закрепления навыков табличного деления полезно включить в устные упражнения задания вида: «Какие числа от 40 до 50 делятся на 6? на 7? на 8?», «Назовите самое большое число до 30, которое делится на 8, на 7», «Назовите по порядку числа, которые делятся на 4, на 3» и т. п. 2. Вычислите. Найдите лишнее выражение: 40 : 5 = 72 : 9 = 64 : 8 = 24 : 4 = 80 : 10 = 32 : 4 = 56 : 7 = 48 : 6 = 3. Арифметические ребусы: 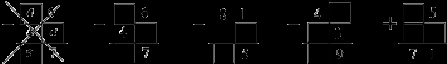 III. Работа над новым материалом. Составление таблицы умножения числа 9 можно провести аналогично тому, как это делалось при составлении таблицы умножения числа 8 (см. урок № 58). Однако, учитывая особую трудность новой таблицы для запоминания (опыт показывает, что больше всего затруднений и ошибок возникает у детей именно при решении примеров на умножение и деление на 9), полезно познакомить учеников с некоторыми специальными приемами, облегчающими вычисления результата для этих случаев. Так, составляя таблицу, полезно провести иллюстрацию с использованием демонстрационных палочек.Например: рассматривается пример 9 · 2. Учитель выставляет на полочке 2 пучка-десятка и говорит: «Я взяла 2 раза по 10, получилось 2 десятка, а надо было взять 2 раза по 9. Выну из каждого пучка по 1 палочке. Всего я вынула 2 палочки, значит, получится 2 десятка без двух, то есть 9 · 2 = 18». Аналогично ведутся демонстрация и рассуждения для случая 9 · 5 и других. На доске делаем запись вида: 9 · 2 – это 2 д. без двух, то есть 18; 9 · 3 – это 3 д. без трех, то есть 27; 9 · 4 – это 4 д. без четырех, то есть 36 и т. д. После того как вся таблица будет составлена и записана на доске, обратить внимание детей на то, что во всех случаях число десятков в ответе на 1 меньше, чем второй множитель, а сумма цифр в записи ответов всегда равна 9. Эти наблюдения, как показывает опыт, предупреждают возникновение многих ошибок, а кроме того, готовят детей к усвоению в дальнейшем признака делимости на 3 и на 9. Запись всей таблицы в тетрадях выполнять не обязательно – можно ограничиться записью лишь тех двух новых примеров, которые на этом уроке встречаются впервые (9 · 9 = 81, 81 : 9 = 9), а затем выполнить задание № 2. Ф и з к у л ь т м и н у т к а Мы становимся всё выше, Достаём руками крыши. На два счёта – поднялись, Три, четыре – руки вниз. IV. Работа над пройденным материалом. 1. Решение задач. Задачу № 3 дети решают сами; учитель может помочь записать условие: 1-й пакет – 15 м. 2-й пакет – 21 м. После этого учащиеся записывают решение и ответ сами. Задачу № 4 учитель разбирает с детьми устно. Учащиеся объясняют, что разделив 27 на 9, узнаем, сколько кроликов получило морковку из первого пакета. Вычислив сумму 27 и 18, узнаем, сколько всего морковок принесла девочка кроликам, а разделив эту сумму на 9, узнаем, сколько кроликов получили морковки. |
