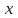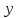Отчет по лабораторным работам по дисциплине Конструирование программ

• Название: Отчет по лабораторным работам по дисциплине Конструирование программ
• Дата: 06.03.2021
• Размер: 356.47 Kb.
• Имя файла: Otchyot.docx
• Тип: Отчет; #182374
• страница: 2 из 9

Лабораторная работа № 2. Интерполирование и экстраполирование данных. Интерполяционный многочлен Лагранжа

В практических расчетах чаще всего используют интерполяционные многочлены невысоких степеней. Из формулы (2.3.4) видно, что единственный, восстанавливаемый без дополнительных условий многочлен Лагранжа должен иметь степень, на единицу меньшую числа точек интерполяционной таблицы. Обычно по исходным данным именно такой многочлен и восстанавливается. По найденному многочлену находят приближенные значения функции для любых значений аргумента, лежащих между узлами заданной сетки.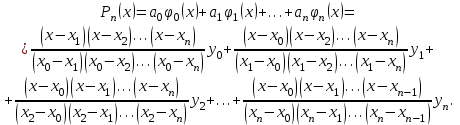
(2.3.3)

Эта формула называется интерполяционной формулой Лагранжа. Приведем ее в сокращенной записи: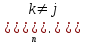

(2.3.4)

Согласно этой схеме интерполяционные многочлены любого вида вычисляются последовательно по формулам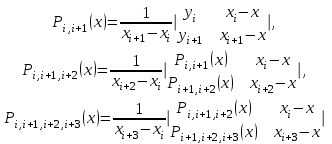



Задание № 1. По образцу разобранного примера восстановить многочлен Лагранжа, удовлетворяющий приведенным исходным данным.

25.

	0	1	2	3
	-3	-2	-1	0
	40	27	12	1

Задание № 2. Используя схему Эйткена, вычислить приближенное значение функции 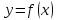, заданной таблично при данном значении аргумента .

№ варианта
5	8.960	6.81	8.0866
10	7.675	7.35	8.9492
15	9.490	8.00	10.2964
20	10.000	8.85	12.0966
25	8.125	9.34	13.4087
30	10.777	9.95	15.2368
		10.25	18.1109
		11.00	21.5445

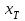Задание №1

#include

#include

using namespace std;

int main()

{

int x[4], y[4], x_x[4][4];

double a[4], b[4], temp;

do

{

for (int i = 0; i < 4; ++i)

{

cout << "x" << i << " = ";

cin >> x[i];

cout << "y" << i << " = ";

cin >> y[i];

}

for (int i = 0; i < 4; ++i)

for (int j = 0; j < 4; ++j)

x_x[i][j] = x[i] - x[j];

for (int i = 0; i < 4; ++i)

{

a[i] = y[i];

for (int j = 0; j < 4; ++j)

if (i != j) a[i] /= x_x[i][j];

}

b[3] = 0;

for (int i = 0; i < 4; ++i) b[3] += a[i];

b[2] = 0;

for (int i = 0; i < 4; ++i)

for (int j = 0; j < 4; ++j)

if (i != j) b[2] -= x[j] * a[i];

b[1] = 0;

for (int i = 0; i < 4; ++i)

for (int j = 0; j < 4; ++j)

if (i != j) for (int k = 0; k < 4; ++k)

if ((i != k) && (j != k)) b[1] += x[j] * x[k] * a[i];

b[1] /= 2;

b[0] = 0;

for (int i = 0; i < 4; ++i)

{

temp = a[i];

for (int j = 0; j < 4; ++j)

if (i != j) temp *= x[j];

b[0] -= temp;

}

cout << b[3] << "x^3+" << b[2] << "x^2+" << b[1] << "x+" << b[0] << endl;

temp = _getch();

} while (temp != 27);

return 0;

}

Задание №2

#include

#include

using namespace std;

int main()

{

const double h = 0.01;

double a[10][8],x;

bool br;

do

{

cout << "x = ";

cin >> x;

for (int i = 0; i < 8; ++i)

{

cout << "x" << i << " = ";

cin >> a[0][i];

cout << "y" << i << " = ";

cin >> a[1][i];

a[2][i] = a[0][i] - x;

}

for (int i = 1; i < 8; ++i)

a[3][i] = (a[1][i - 1] * a[2][i] - a[1][i] * a[2][i - 1]) / (a[0][i] - a[0][i - 1]);

for (int j = 4; j < 10; ++j)

{

for (int i = j - 2; i < 8; ++i)

{

a[j][i] = (a[j-1][i - j + 2] * a[2][i] - a[j-1][i] * a[2][i - j + 2]) / (a[0][i] - a[0][i - j + 2]);

if (((a[j][i] - a[j - 1][i]) < h) || ((a[j][i] - a[j - 1][i - 1]) < h))

{

cout << "y(" << x << ") = " << round(a[j][i] / h)*h << endl;

br = true;

break;

}

}

if (br) break;

}

x = _getch();

} while (x != 27);

return 0;

}