Отчет по лабораторным работам по дисциплине Конструирование программ
 Скачать 356.47 Kb. Скачать 356.47 Kb.
|
Лабораторная работа № 5. Численное дифференцирование и численное интегрирование функцийЧисленное дифференцирование применяется в тех случаях, когда либо невозможно, либо очень сложно или дорого продифференцировать функцию аналитически. Из-за быстрого накопления ошибок при численном вычислении старших производных обычно ограничиваются нахождением первой и второй производной по формулам (4.1.1), (4.1.2) и (4.1.5). Из определения первой производной 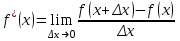 естественно использовать для ее вычисления две простейшие приближенные формулы естественно использовать для ее вычисления две простейшие приближенные формулы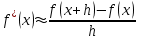 , (4.1.1) , (4.1.1)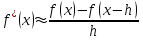 , (4.1.2) , (4.1.2)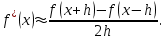 (4.1.5) (4.1.5)В прикладных исследованиях, когда возникает необходимость вычисления 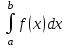 и первообразной не существует, приходиться интеграл считать численно. Наиболее широко на практике используются квадратурные формулы - приближенные равенства вида и первообразной не существует, приходиться интеграл считать численно. Наиболее широко на практике используются квадратурные формулы - приближенные равенства вида 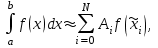 (4.5.1) (4.5.1)где 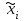 - некоторые точки из отрезка - некоторые точки из отрезка 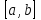 - узлы квадратурной формулы (4.5.1), - узлы квадратурной формулы (4.5.1), 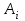 - числовые коэффициенты, называемые весами квадратурной формулы, - числовые коэффициенты, называемые весами квадратурной формулы, 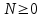 - целое число. Сумма - целое число. Сумма 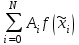 , которая принимается за приближенное значение интеграла, называется квадратурной суммой. , которая принимается за приближенное значение интеграла, называется квадратурной суммой. Задание № 1. Для данных функций построить правую, левую и центральную первые разностные производные, вторую разностную производную на указанном интервале с данными шагами сетки 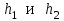 и сравнить полученные значения с точными значениями производных: и сравнить полученные значения с точными значениями производных:25. 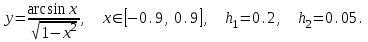 Задание № 2. Найти численное значение интеграла от функций, указанных в задании № 1, на заданном промежутке. При вычислении по подпрограмме parab выбрать 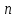 , соответствующее меньшему значению шага. , соответствующее меньшему значению шага. Код программы #include #include using namespace std; double arcsin(double x) { double result = x, prev, temp, a = x; int i = 1; do { prev = result; temp = 1; a *= x*x; for (int j = 1; j <= i; ++j) temp = temp * ((2 * j - 1) * (2 * j) )/ (4 * j * j); temp /= 2 * i + 1; result += temp * a; ++i; } while ((result - prev) > 0.00001); return result; } double func(double x) { return arcsin(x) / sqrt(1 - x*x); } int main() { setlocale(LC_ALL, "rus"); double x1, x2, h1, h2, x; do { cout << "x1 = "; cin >> x1; cout << "x2 = "; cin >> x2; cout << "h1 = "; cin >> h1; cout << "h2 = "; cin >> h2; cout << "Задание 1" << endl; cout << "Шаг равен " << h1 << endl; x = x1; do { cout << "x = " << x << "; f'r = " << (func(x + h1) - func(x)) / h1 << "; f'l = " << (func(x) - func(x - h1)) / h1 << "; f' = " << (func(x + h1) - func(x - h1)) / (h1 + h1) << "; f'' = " << (func(x - h1) - 2 * func(x) + func(x + h1)) / (h1 * h1) << endl; x += h1; } while (x <= x2); cout << "Шаг равен " << h2 << endl; x = x1; do { cout << "x = " << x << "; f'r = " << (func(x + h2) - func(x)) / h2 << "; f'l = " << (func(x) - func(x - h2)) / h2 << "; f' = " << (func(x + h2) - func(x - h2)) / (h2 + h2) << "; f'' = " << (func(x - h2) - 2 * func(x) + func(x + h2)) / (h2 * h2) << endl; x += h2; } while (x <= x2); cout << "Задание 2" << endl; double result = 0; x = x1; do { result += func(x + h2 / 2); x += h2; } while (x < x2); cout << "Формула центральных прямоугольников: Интеграл равен " << result * h2 << endl; result = func(x1) / 2; x = x1 + h2; do { result += func(x); x += h2; } while (x < x2 - h2); result += func(x) / 2; cout << "Формула трапеций: Интеграл равен " << result * h2 << endl; result = func(x1); x = x1 + h2; do { result += 4 * func(x - h2 / 2) + 2 * func(x); x += h2; } while (x < x2 - h2); result += func(x) + 4 * func(x - h2 / 2); cout << "Формула парабол: Интеграл равен " << result * h2 / 6 << endl; x = _getch(); } while (x != 27); return 0; } |
