|
|
Отчет по лабораторным работам по дисциплине Конструирование программ
Задача Коши для отдельного дифференциального уравнения решается сравнительно редко. Чаще приходится интегрировать систему обыкновенных дифференциальных уравнений. Дифференциальные уравнения высших порядков также легко сводятся к системе уравнений. Если задано уравнение 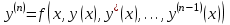 с начальными условиями с начальными условиями 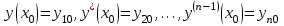 , то стандартная замена переменных , то стандартная замена переменных 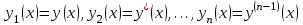 приводит это уравнение к системе приводит это уравнение к системе 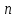 дифференциальных уравнений первого порядка: дифференциальных уравнений первого порядка:
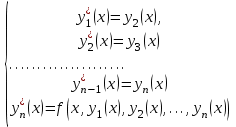 (7.11.1) (7.11.1)
с начальными условиями 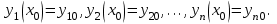
Расчетная формула метода Эйлера 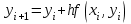 применительно к системе (7.9.3) примет вид применительно к системе (7.9.3) примет вид
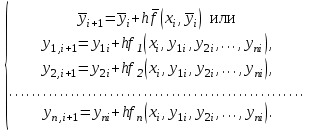 (7.9.6) (7.9.6)
Метод Рунге - Кутты четвертого порядка точности (7.4.13) порождает следующие формулы:
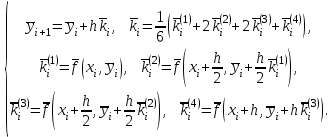 (7.9.7) (7.9.7)
Теория численных методов решения задачи Коши для систем дифференциальных уравнений имеет много общего с соответствующей теорией решения задачи Коши для одного дифференциального уравнения.
Задание № 1. С помощью любой из разобранных в лабораторной работе подпрограмм решить задачу Коши для системы дифференциальных уравнений на заданном отрезке:
25. 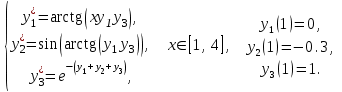
Код программы
#include
#include
using namespace std;
double exp(double x)
{
double y = 1, prev, a = 1, fact = 1;
int i = 1;
const double E = 0.00001;
do
{
prev = y;
a *= x;
fact *= i;
++i;
y += a / fact;
} while ((y - prev) > E);
return y;
}
double arctg(double x)
{
double y = x, prev, a = x;
int i = 2;
const double E = 0.00001;
do
{
prev = y;
a *= x*x;
if (i % 2) y += a / (2 * i - 1);
else y -= a / (2 * i - 1);
++i;
} while (abs(y - prev) > E);
return y;
}
double sin(double x)
{
double y = x, prev, a = x, fact = 1;
int i = 2;
const double E = 0.00001;
do
{
prev = y;
a *= x*x;
fact *= i*(i + 1);
if (i % 2) y += a / fact;
else y -= a / fact;
++i;
} while (abs(y - prev) > E);
return y;
}
double f1(double x, double y1, double y2, double y3)
{
return arctg(x*y1*y3);
}
double f2(double x, double y1, double y2, double y3)
{
return sin(arctg(y1*y3));
}
double f3(double x, double y1, double y2, double y3)
{
return exp(-y1*y3*y2);
}
int main()
{
setlocale(LC_ALL, "rus");
double x1 = 1, x2 = 4, h = 0.1, y1 = 0, y2 = -0.3, y3 = 1, x = x1;
cout << "Метод Эйлера" << endl;
cout << "x = 1; y1 = 0; y2 = -0.3; y3 = 1" << endl;
do
{
x += h;
y1 += h*f1(x, y1, y2, y3);
y2 += h*f2(x, y1, y2, y3);
y3 += h*f3(x, y1, y2, y3);
cout << "x = " << x << "; y1 = " << y1 << "; y2 = " << y2 << "; y3 = " << y3 << endl;
} while (x <= x2);
cout << "Метод Рунге - Кутты" << endl;
double k[3][4];
y1 = 0;
y2 = -0.3;
y3 = 1;
x = 1;
cout << "x = 1; y1 = 0; y2 = -0.3; y3 = 1" << endl;
do
{
k[0][0] = f1(x, y1, y2, y3);
k[1][0] = f2(x, y1, y2, y3);
k[2][0] = f3(x, y1, y2, y3);
x += h / 2;
k[0][1] = f1(x, y1 + h*k[0][0] / 2, y2 + h*k[1][0] / 2, y3 + h*k[2][0] / 2);
k[1][1] = f2(x, y1 + h*k[0][0] / 2, y2 + h*k[1][0] / 2, y3 + h*k[2][0] / 2);
k[2][1] = f3(x, y1 + h*k[0][0] / 2, y2 + h*k[1][0] / 2, y3 + h*k[2][0] / 2);
k[0][2] = f1(x, y1 + h*k[0][1] / 2, y2 + h*k[1][1] / 2, y3 + h*k[2][1] / 2);
k[1][2] = f2(x, y1 + h*k[0][1] / 2, y2 + h*k[1][1] / 2, y3 + h*k[2][1] / 2);
k[2][2] = f3(x, y1 + h*k[0][1] / 2, y2 + h*k[1][1] / 2, y3 + h*k[2][1] / 2);
x += h / 2;
k[0][3] = f1(x, y1 + h*k[0][2], y2 + h*k[1][2], y3 + h*k[2][2]);
k[1][3] = f2(x, y1 + h*k[0][2], y2 + h*k[1][2], y3 + h*k[2][2]);
k[2][3] = f3(x, y1 + h*k[0][2], y2 + h*k[1][2], y3 + h*k[2][2]);
y1 += h * (k[0][0] + 2 * k[0][1] + 2 * k[0][2] + k[0][3]) / 6;
y2 += h * (k[1][0] + 2 * k[1][1] + 2 * k[1][2] + k[1][3]) / 6;
y3 += h * (k[2][0] + 2 * k[2][1] + 2 * k[2][2] + k[2][3]) / 6;
cout << "x = " << x << "; y1 = " << y1 << "; y2 = " << y2 << "; y3 = " << y3 << endl;
} while (x < x2 - h);
_getch();
return 0;
}
Лабораторная работа № 11. Решение задачи Дирихле
для уравнения Лапласа методом сеток
Найти приближенное решение уравнения Лапласа
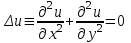 (8.9.1) (8.9.1)
в квадрате 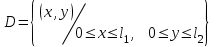 , принимающее на границе области , принимающее на границе области 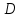 заданные краевые условия (8.3.7) и (8.3.8): заданные краевые условия (8.3.7) и (8.3.8):
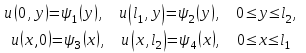 (8.9.2) (8.9.2)
Построим область решения, покроем ее сеткой с шагом 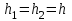 , , 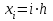 , , 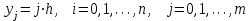 и вычислим значения искомой функции и вычислим значения искомой функции 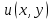 в граничных точках области по формулам (8.9.2). Введем обозначения в граничных точках области по формулам (8.9.2). Введем обозначения 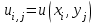 и аппроксимируем частные производные и аппроксимируем частные производные 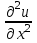 и и 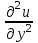 в каждом внутреннем узле сетки центральными разностными производными второго порядка по формулам (8.6.7) и (8.6.8): в каждом внутреннем узле сетки центральными разностными производными второго порядка по формулам (8.6.7) и (8.6.8):
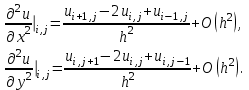 (8.9.3) (8.9.3)
Уравнение Лапласа (8.9.1) заменим конечно-разностным уравнением
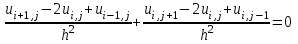 . (8.9.4) . (8.9.4)
Погрешность замены дифференциального уравнения разностным составляет величину 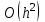 . Уравнение (8.9.4) вместе со значениями . Уравнение (8.9.4) вместе со значениями 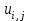 в граничных узлах образуют систему линейных алгебраических уравнений относительно приближенных значений в граничных узлах образуют систему линейных алгебраических уравнений относительно приближенных значений 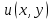 в узлах сетки: в узлах сетки:
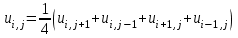 . (8.9.5) . (8.9.5)
При получении сеточных уравнений (8.9.5) использовалась схема узлов, изображенная на
с. 208.
Численное решение задачи Дирихле для уравнения Лапласа в области 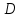 состоит в нахождении приближенных значений состоит в нахождении приближенных значений 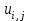 искомой функции искомой функции 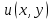 во внутренних узлах сетки. Для определения величин во внутренних узлах сетки. Для определения величин 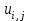 необходимо решить систему линейных алгебраических уравнений (8.9.5). необходимо решить систему линейных алгебраических уравнений (8.9.5).
В данной лабораторной работе система (8.9.5) решается методом простых итераций (см. подразд. 5.5) по формулам
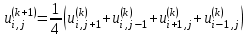 , (8.9.6) , (8.9.6)
где верхним индексом 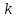 обозначен номер итерации. В качестве условия окончания итерационного процесса можно принять обозначен номер итерации. В качестве условия окончания итерационного процесса можно принять
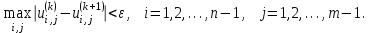 (8.9.7) (8.9.7)
Как следует из теории, изложенной в подразд. 8.6, описанная разностная схема обладает свойством устойчивости и сходимости. Это означает, что, выбрав достаточно малый шаг 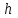 , можно сколь угодно точно решить исходную задачу. , можно сколь угодно точно решить исходную задачу.
Задание № 1. С помощью подпрограммы Dirichlet найти приближенное решение уравнения Лапласа в заданной области 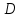 с указанными граничными условиями. с указанными граничными условиями.
25. 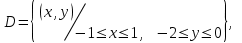
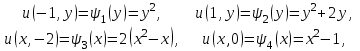
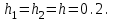
Код программы
#include
#include
using namespace std;
double psi1(double y)
{
return y*y;
}
double psi2(double y)
{
return y*y + 2 * y;
}
double psi3(double x)
{
return 2 * (x*x - x);
}
double psi4(double x)
{
return x*x - 1;
}
int main()
{
double x1 = -1, x2 = 1, y1 = -2, y2 = 0, h = 0.2, u[11][11], E = 0.001, l, next;
bool rep;
cout.precision(3);
for (int i = 0; i < 11; ++i)
u[0][i] = psi1(y1 + h * i);
for (int i = 0; i < 11; ++i)
u[10][i] = psi2(y1 + h * i);
for (int i = 0; i < 11; ++i)
u[i][0] = psi3(x1 + h * i);
for (int i = 0; i < 11; ++i)
u[i][10] = psi4(x1 + h * i);
for (int i = 1; i < 10; ++i)
{
l = (u[10][i] - u[0][i]) / 10;
for (int j = 1; j < 10; ++j)
u[j][i] = u[0][i] + j*l;
}
do
{
rep = false;
for (int i = 1; i < 10; ++i)
for (int j = 1; j < 10; ++j)
{
next = (u[i][j - 1] + u[i][j + 1] + u[i - 1][j] + u[i + 1][j]) / 4;
if (abs(next - u[i][j]) > E) rep = true;
u[i][j] = next;
}
} while (rep);
for (int i = 0; i < 11; ++i)
{
for (int j = 0; j < 11; ++j)
cout << u[j][i] << " ";
cout << endl;
}
_getch();
return 0;
}
Лабораторная работа № 12. Решение однородного уравнения колебаний струны методом сеток по неявной схеме.
Уравнение гиперболического типа
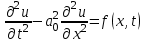 (8.10.1) (8.10.1)
описывает поперечные колебания упругой натянутой струны. Его решение – функция 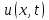 дает смещение участков струны в поперечном направлении. дает смещение участков струны в поперечном направлении.
Решим пример на это уравнение при условии 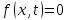 . Задача состоит в отыскании функции . Задача состоит в отыскании функции 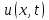 , удовлетворяющей в прямоугольнике , удовлетворяющей в прямоугольнике 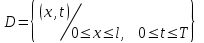 при при 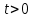 уравнению уравнению
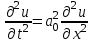 , (8.10.2) , (8.10.2)
начальным условиям
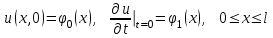 (8.10.3) (8.10.3)
и краевым условиям
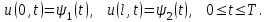 (8.10.4) (8.10.4)
Для реализации разностной схемы решения задачи (8.10.2) – (8.10.4) построим в области 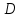 сетку сетку 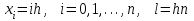 , , 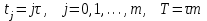 и аппроксимируем производные от решения в узлах и аппроксимируем производные от решения в узлах 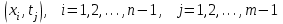 с помощью центральных разностных отношений (8.5.11) и (8.5.12) на пятиточечном шаблоне, изображенном на с. 206. Этот шаблон не требует выполнения какого-либо соотношения между шагами с помощью центральных разностных отношений (8.5.11) и (8.5.12) на пятиточечном шаблоне, изображенном на с. 206. Этот шаблон не требует выполнения какого-либо соотношения между шагами 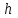 и и 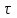 для обеспечения устойчивости решения. для обеспечения устойчивости решения.
Получим приближенное уравнение
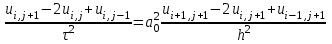 . (8.10.5) . (8.10.5)
Погрешность замены дифференциального уравнения (8.10.2) разностным (8.10.5) составляет величину 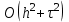 . Полагая . Полагая 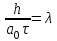 , получаем трехслойную разностную схему , получаем трехслойную разностную схему
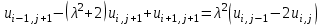 . (8.10.6) . (8.10.6)
Эта схема называется трехслойной потому, что связывает между собой приближенные значения 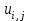 функции функции 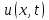 на трех временных слоях с номерами на трех временных слоях с номерами 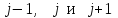 . .
Система линейных алгебраических уравнений (8.10.6) обладает трехдиагональной матрицей и решается методом прогонки. Например, при 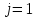 система уравнений (8.10.6) приобретает вид система уравнений (8.10.6) приобретает вид
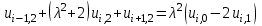 . (8.10.7) . (8.10.7)
Значения 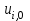 известны из начальных условий (8.10.3), а для определения известны из начальных условий (8.10.3), а для определения 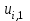 можно исполь- можно исполь-
зовать один из возможных приемов, например,
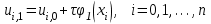 . (8.10.8) . (8.10.8)
Задание № 1. Найти приближенное решение однородного уравнения гиперболического типа 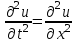 в квадрате в квадрате 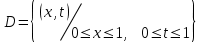 с шагом с шагом 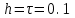 , используя программы , используя программы 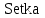 и и 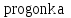 . .
25. 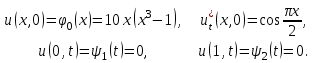
Код программы
#include
#include
using namespace std;
double cos(double x)
{
double y = 1, prev, a = 1, fact = 1;
int i = 1;
const double E = 0.0001;
do
{
prev = y;
a *= x*x;
for (int j = 2 * (i - 1) + 1; j <= 2 * i; ++j)
fact *= j;
if (i % 2) y -= a / fact;
else y += a / fact;
++i;
} while (abs(y - prev) > E);
return y;
}
double phi(double x)
{
return 10 * x*(x*x*x - 1);
}
double ut(double x){return cos(3.1415926*x / 2);}
int main()
{
cout.precision(3);
double h = 0.1, x1 = 0, x2 = 1, t1 = 0, t2 = 1, u[11][11];
for (int i = 0; i < 11; ++i)
{
u[0][i] = 0;
u[10][i] = 0;
}
for (int i = 1; i < 10; ++i)
u[i][0] = phi(x1 + i*h);
for (int i = 1; i < 10; ++i)
u[i][1] = u[0][i] + ut(x1 + i*h);
double prev[9], b[9], E = 0.001, temp;
for (int k = 2; k < 11; ++k)
{
for (int i = 0; i < 9; ++i)
{
b[i] = u[i + 1][k - 2] - 2 * u[i + 1][k - 1];
u[i + 1][k] = 0;
}
do
{
temp = 0;
for (int i = 0; i < 9; ++i)
{
prev[i] = u[i + 1][k];
u[i + 1][k] = (b[i] - u[i][k] - u[i + 2][k]) / 3;
if (abs(prev[i] - u[i + 1][k]) > temp) temp = abs(prev[i] - u[i + 1][k]);
}
} while (temp > E);
}
for (int i = 0; i < 11; ++i)
{
for (int j = 0; j < 11; ++j)
cout << u[j][i] << " ";
cout << endl;
}
_getch();
return 0;
} |
|
|
 Скачать 356.47 Kb.
Скачать 356.47 Kb. с начальными условиями
с начальными условиями 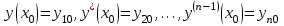 , то стандартная замена переменных
, то стандартная замена переменных 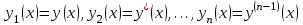 приводит это уравнение к системе
приводит это уравнение к системе 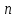 дифференциальных уравнений первого порядка:
дифференциальных уравнений первого порядка: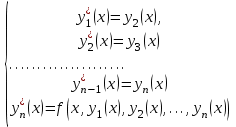 (7.11.1)
(7.11.1)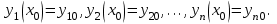
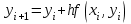 применительно к системе (7.9.3) примет вид
применительно к системе (7.9.3) примет вид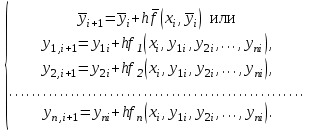 (7.9.6)
(7.9.6)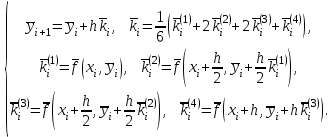 (7.9.7)
(7.9.7)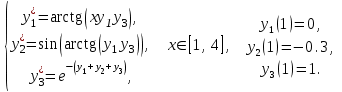

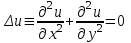 (8.9.1)
(8.9.1)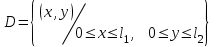 , принимающее на границе области
, принимающее на границе области 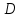 заданные краевые условия (8.3.7) и (8.3.8):
заданные краевые условия (8.3.7) и (8.3.8):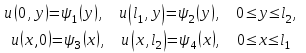 (8.9.2)
(8.9.2)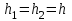 ,
, 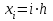 ,
, 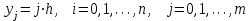 и вычислим значения искомой функции
и вычислим значения искомой функции 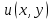 в граничных точках области по формулам (8.9.2). Введем обозначения
в граничных точках области по формулам (8.9.2). Введем обозначения 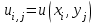 и аппроксимируем частные производные
и аппроксимируем частные производные 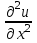 и
и 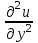 в каждом внутреннем узле сетки центральными разностными производными второго порядка по формулам (8.6.7) и (8.6.8):
в каждом внутреннем узле сетки центральными разностными производными второго порядка по формулам (8.6.7) и (8.6.8):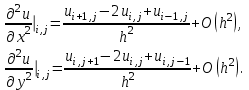 (8.9.3)
(8.9.3)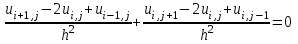 . (8.9.4)
. (8.9.4)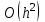 . Уравнение (8.9.4) вместе со значениями
. Уравнение (8.9.4) вместе со значениями 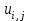 в граничных узлах образуют систему линейных алгебраических уравнений относительно приближенных значений
в граничных узлах образуют систему линейных алгебраических уравнений относительно приближенных значений 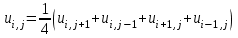 . (8.9.5)
. (8.9.5)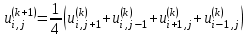 , (8.9.6)
, (8.9.6)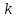 обозначен номер итерации. В качестве условия окончания итерационного процесса можно принять
обозначен номер итерации. В качестве условия окончания итерационного процесса можно принять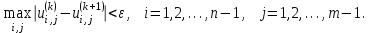 (8.9.7)
(8.9.7)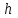 , можно сколь угодно точно решить исходную задачу.
, можно сколь угодно точно решить исходную задачу.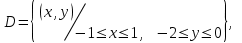
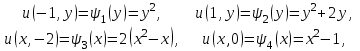
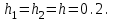
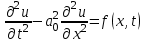 (8.10.1)
(8.10.1)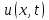 дает смещение участков струны в поперечном направлении.
дает смещение участков струны в поперечном направлении.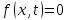 . Задача состоит в отыскании функции
. Задача состоит в отыскании функции 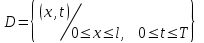 при
при 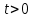 уравнению
уравнению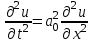 , (8.10.2)
, (8.10.2)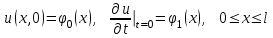 (8.10.3)
(8.10.3)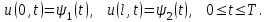 (8.10.4)
(8.10.4)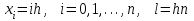 ,
, 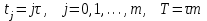 и аппроксимируем производные от решения в узлах
и аппроксимируем производные от решения в узлах 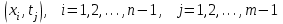 с помощью центральных разностных отношений (8.5.11) и (8.5.12) на пятиточечном шаблоне, изображенном на с. 206. Этот шаблон не требует выполнения какого-либо соотношения между шагами
с помощью центральных разностных отношений (8.5.11) и (8.5.12) на пятиточечном шаблоне, изображенном на с. 206. Этот шаблон не требует выполнения какого-либо соотношения между шагами 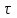 для обеспечения устойчивости решения.
для обеспечения устойчивости решения.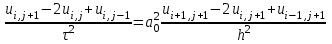 . (8.10.5)
. (8.10.5)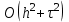 . Полагая
. Полагая 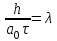 , получаем трехслойную разностную схему
, получаем трехслойную разностную схему 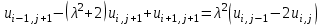 . (8.10.6)
. (8.10.6)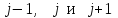 .
.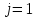 система уравнений (8.10.6) приобретает вид
система уравнений (8.10.6) приобретает вид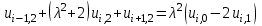 . (8.10.7)
. (8.10.7)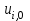 известны из начальных условий (8.10.3), а для определения
известны из начальных условий (8.10.3), а для определения 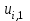 можно исполь-
можно исполь-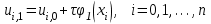 . (8.10.8)
. (8.10.8)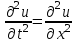 в квадрате
в квадрате 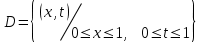 с шагом
с шагом 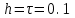 , используя программы
, используя программы 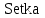 и
и 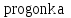 .
.