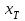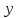Отчет по лабораторным работам по дисциплине Конструирование программ
 Скачать 356.47 Kb. Скачать 356.47 Kb.
|
Лабораторная работа № 3. Интерполирование и экстраполирование данных. Интерполяционный многочлен НьютонаИнтерполяционный многочлен Ньютона является другой формой записи единого интерполяционного многочлена. Применение многочлена Ньютона имеет практические преимущества по сравнению с формулой Лагранжа и в случае неравноотстоящих, и особенно в случае равноотстоящих узлов. Алгебраический многочлен 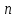 -й степени -й степени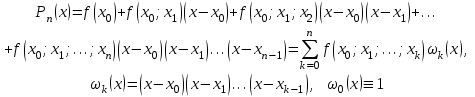 (2.7.1) (2.7.1)называется интерполяционным многочленом Ньютона с разделенными разностями. Очевидна аналогия формулы (2.7.1) с формулой Тейлора. Действительно, так как по теореме 2.7 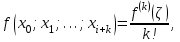 то то 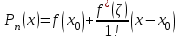 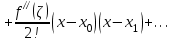 Формулы подраздела 2.4 о погрешности интерполяции Формулы подраздела 2.4 о погрешности интерполяции 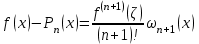 в точке в точке 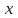 , не являющейся узловой, можно уточнить следующим образом: , не являющейся узловой, можно уточнить следующим образом: 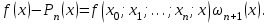 Задание № 1. Построить интерполяционный многочлен Ньютона по неравноотстоящей сетке узлов и найти приближенное значение интерполируемой функции 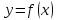 при значении аргумента при значении аргумента 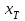 . .
Задание_№_2.'>Задание № 2. Вычислить приближенное значение функции 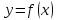 по интерполяционной формуле Ньютона для интерполяции вперед или назад. по интерполяционной формуле Ньютона для интерполяции вперед или назад.
Задание №1 #include #include using namespace std; int main() { double a[9][8], x, b[8]; do { for (int i = 0; i < 8; ++i) { cout << "x" << i << " = "; cin >> a[0][i]; cout << "y" << i << " = "; cin >> a[1][i]; } for (int i = 2; i < 9; ++i) for (int j = 0; j < 9 - i; ++j) a[i][j] = (a[i - 1][j + 1] - a[i - 1][j]) / (a[0][i+j-1] - a[0][j]); for (int z = 7; z >= 0; --z) { b[z] = a[z + 1][0]; if (z == 7) continue; for (int i = 0; i < z + 1; ++i) b[z] -= a[z+2][0] * a[0][i]; if (z == 6) continue; for (int i = 0; i < z + 2; ++i) for (int j = 0; j < i; ++j) b[z] += a[z+3][0] * a[0][i] * a[0][j]; if (z == 5) continue; for (int i = 0; i < z + 3; ++i) for (int j = 0; j < i; ++j) for (int k = 0; k < j; ++k) b[z] -= a[z + 4][0] * a[0][i] * a[0][j] * a[0][k]; if (z == 4) continue; for (int i = 0; i < z + 4; ++i) for (int j = 0; j < i; ++j) for (int k = 0; k < j; ++k) for (int l = 0; l < k; ++l) b[z] += a[z + 5][0] * a[0][i] * a[0][j] * a[0][k] * a[0][l]; if (z == 3) continue; for (int i = 0; i < z + 5; ++i) for (int j = 0; j < i; ++j) for (int k = 0; k < j; ++k) for (int l = 0; l < k; ++l) for (int s = 0; s < l; ++s) b[z] -= a[z + 6][0] * a[0][i] * a[0][j] * a[0][k] * a[0][l] * a[0][s]; if (z == 2) continue; for (int i = 0; i < z + 6; ++i) for (int j = 0; j < i; ++j) for (int k = 0; k < j; ++k) for (int l = 0; l < k; ++l) for (int s = 0; s < l; ++s) for (int u = 0; u < s; ++u) b[z] += a[z + 7][0] * a[0][i] * a[0][j] * a[0][k] * a[0][l] * a[0][s] * a[0][u]; } b[0] -= a[8][0] * a[0][0] * a[0][1] * a[0][2] * a[0][3] * a[0][4] * a[0][5] * a[0][6]; for (int i = 7; i >= 1; --i) cout << b[i] << "x^" << i << "+"; cout << b[0] << endl; do { cout << "x = "; cin >> x; double temp = 1, result = 0; result += b[0]; for (int i = 1; i < 8; ++i) { temp *= x; result += temp*b[i]; } cout << "y(" << x << ") = " << result << endl; x = _getch(); } while (x != 27); x = _getch(); } while (x != 27); return 0; } Задание №2. #include #include using namespace std; int fact(int n) { if (n == 1) return 1; else return n*fact(n - 1); } int main() { double a[6][10], x, q, h, result, temp; int k; do { cout << "x = "; cin >> x; for (int i = 0; i < 10; ++i) { cout << "x" << i << " = "; cin >> a[0][i]; cout << "y" << i << " = "; cin >> a[1][i]; } h = a[0][1] - a[0][0]; for (int j = 2; j < 6; ++j) for (int i = 0; i < 9; ++i) a[j][i] = a[j - 1][i + 1] - a[j - 1][i]; if (x > a[0][4]) { for (k = 5; k < 10; ++k) if (a[0][k] > x) break; q = (x - a[0][k]) / h; result = a[1][k]; temp = 1; for (int i = 1; i < 5; ++i) { temp *= q + i - 1; result += a[i + 1][k - i] / fact(i)*temp; } } else { for (k = 4; k > 0; --k) if (a[0][k] < x) break; q = (x - a[0][k]) / h; result = a[1][k]; temp = 1; for (int i = 1; i < 5; ++i) { temp *= q - i + 1; result += a[i+1][k-1] / fact(i)*temp; } } cout << "y(" << x << ") = " << result << endl; x = _getch(); } while (x != 27); } |