Отчет по лабораторным работам по дисциплине Конструирование программ
 Скачать 356.47 Kb. Скачать 356.47 Kb.
|
Лабораторная работа № 9. Методы интегрирования обыкновенных дифференциальных уравненийСуществует большое число методов приближенного решения дифференциальных уравнений, основанных на самых различных идеях. Численные методы дают приближенное решение 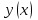 в виде таблицы значений в виде таблицы значений 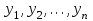 в точках в точках 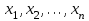 . .Простейшим методом численного интегрирования дифференциального уравнения первого порядка 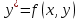 , удовлетворяющего начальному условию , удовлетворяющего начальному условию 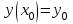 , является метод Эйлера. В нем величины , является метод Эйлера. В нем величины 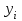 вычисляются по формуле вычисляются по формуле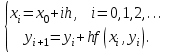 Метод Эйлера относится к группе одношаговых, в которых для расчета точки 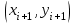 требуется информация только о последней вычисленной точке требуется информация только о последней вычисленной точке 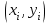 . Геометрическая интерпретация метода изложена в подразд. 7.4. . Геометрическая интерпретация метода изложена в подразд. 7.4.Методы Рунге - Кутты обладают следующими отличительными свойствами: 1) являются одношаговыми: чтобы найти 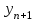 нужна информация только о предыдущей точке нужна информация только о предыдущей точке 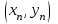 ; ; 2) согласуются с рядом Тейлора вплоть до членов порядка 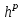 , где степень , где степень 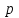 различна для различных методов и называется порядком метода; различна для различных методов и называется порядком метода;3) не требуют вычисления производных от 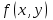 , а только вычисления функции. , а только вычисления функции.Именно благодаря третьему свойству методы Рунге - Кутты более известны, нежели ряд Тейлора. Однако для вычисления одной последующей точки решения приходится вычислять 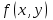 несколько раз при различных значениях несколько раз при различных значениях 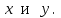 Классический метод Рунге - Кутты описывается системой следующих шести уравнений: 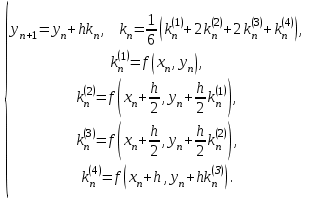 (7.4.13) (7.4.13)Ошибка метода 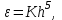 при его использовании функцию необходимо вычислять дважды. при его использовании функцию необходимо вычислять дважды.Существуют более точные методы оценки погрешности интегрирования, основанные на использовании для контроля точности двух различных методов Рунге - Кутты. Один из самых эффективных - метод Рунге - Кутты - Фельберга. В этом методе для оценки погрешности метода пятого порядка используются формулы метода четвертого порядка точности, причем на одном шаге интегрирования требуется всего лишь шесть вычислений значений правой части 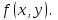 Задание № 1. Решить заданное дифференциальное уравнение первого порядка методом Эйлера и Рунге – Кутты четвертого порядка на отрезке 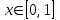 с шагом с шагом 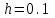 и оценить погрешность интегрирования по правилу Рунге. и оценить погрешность интегрирования по правилу Рунге.25. 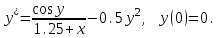 Код программы #include #include using namespace std; double cos(double x) { double y = 1, prev, a = 1, fact = 1; int i=1; const double E = 0.0001; do { prev = y; a *= x*x; for (int j = 2 * (i - 1) + 1; j <= 2 * i; ++j) fact *= j; if (i % 2) y -= a / fact; else y += a / fact; ++i; } while (abs(y - prev) > E); return y; } double func(double x, double y) { return cos(y) / (1.25 + x) - 0.5*y*y; } int main() { setlocale(LC_ALL, "rus"); double x1 = 0, x2 = 1, h = 0.1, x = x1 + h, y = 0, prev; cout << "Метод Эйлера" << endl; cout << "x = 0; y = 0" << endl; do { y += h*func(x, y); cout << "x = " << x << "; y = " << y << endl; x += h; } while (x <= x2); cout << "Метод Рунге - Кутты" << endl; double A[4][3]; A[0][0] = x1; A[0][1] = 0; cout << "x = 0; y = 0" << endl; do { A[2][0] = A[1][0] = A[0][0] + h / 2; A[3][0] = A[0][0] + h; A[0][2] = func(A[0][0], A[0][1]); A[1][1] = A[0][1] + h / 2 * A[0][2]; A[1][2] = func(A[1][0], A[1][1]); A[2][1] = A[0][1] + h / 2 * A[1][2]; A[2][2] = func(A[2][0], A[2][1]); A[3][1] = A[0][1] + h * A[2][2]; A[3][2] = func(A[3][0], A[3][1]); A[0][1] += h*(A[0][2] + 2 * A[1][2] + 2 * A[2][2] + A[3][2])/6; A[0][0] += h; cout << "x = " << A[0][0] << "; y = " << A[0][1] << endl; } while (A[0][0] <= x2-h); _getch(); return 0; } |
