Отчет по лабораторным работам по дисциплине Конструирование программ
 Скачать 356.47 Kb. Скачать 356.47 Kb.
|
Лабораторная работа № 4. Аппроксимация функции по методу наименьших квадратовОчень часто при анализе эмпирических данных необходимо найти явную функциональную зависимость между двумя величинами 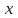 и и 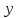 , полученными в результате измерений. Поскольку опытные данные всегда содержат ошибки, то строить интерполяционный многочлен , полученными в результате измерений. Поскольку опытные данные всегда содержат ошибки, то строить интерполяционный многочлен 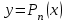 не рационально, так как при интерполяции ошибки повторяются. Желательно по возможности сгладить и минимизировать ошибки наблюдений. Этот результат достигается построением многочлена наилучшего среднего квадратического приближения по методу наименьших квадратов. не рационально, так как при интерполяции ошибки повторяются. Желательно по возможности сгладить и минимизировать ошибки наблюдений. Этот результат достигается построением многочлена наилучшего среднего квадратического приближения по методу наименьших квадратов. Итак, если 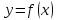 аппроксимируется многочленом вида аппроксимируется многочленом вида 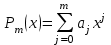 , так что система базисных функций имеет вид , так что система базисных функций имеет вид 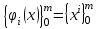 , то неизвестные коэффициенты многочлена , то неизвестные коэффициенты многочлена 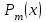 по методу наименьших квадратов определяются из решения системы по методу наименьших квадратов определяются из решения системы 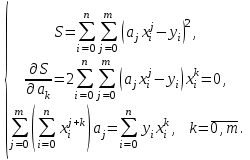 Задание № 1. По методу наименьших квадратов аппроксимировать таблично заданную функцию 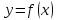 многочленом наилучшего среднеквадратического приближения многочленом наилучшего среднеквадратического приближения 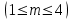 . .
Код программы #include #include using namespace std; double det(double *line1, double *line2, double *line3, double *line4, double *line5, int deg) { if (deg == 1) return line1[0]; else { double result = 0; int i = deg; result += line1[0] * det(line2 + 1, line3 + 1, line4 + 1, line5 + 1, NULL, deg - 1); result -= line2[0] * det(line1 + 1, line3 + 1, line4 + 1, line5 + 1, NULL, deg - 1); i -= 2; if (i == 0) return result; result -= line3[0] * det(line1 + 1, line2 + 1, line4 + 1, line5 + 1, NULL, deg - 1); i--; if (i == 0) return result; result -= line4[0] * det(line1 + 1, line2 + 1, line3 + 1, line5 + 1, NULL, deg - 1); i--; if (i == 0) return result; result -= line5[0] * det(line1 + 1, line2 + 1, line3 + 1, line4 + 1, NULL, deg - 1); return result; } } int main() { double a[13][21], temp, line[6][5], d, c[5]; // 8 иксов и 5 икс-игриков do { for (int i = 0; i < 20; ++i) { cout << "x" << i << " = "; cin >> a[0][i]; for (int j = 1; j < 8; ++j) a[j][i] = a[j - 1][i] * a[0][i]; cout << "y" << i << " = "; cin >> a[8][i]; for (int j = 9; j < 13; ++j) a[j][i] = a[j - 1][i] * a[0][i]; } for (int i = 0; i < 13; ++i) { temp = 0; for (int j = 0; j < 20; ++j) temp += a[i][j]; a[i][20] = temp; } line[0][0] = 20; for (int i = 1; i < 5; ++i) line[0][i] = a[i-1][20]; for (int i = 1; i < 5; ++i) for (int j = 0; j < 5; ++j) line[i][j] = a[i + j][20]; for (int i = 0; i < 5; ++i) line[5][i] = a[i + 8][20]; for (int i = 2; i < 5; ++i) { d = det(line[0], line[1], line[2], line[3], line[4], i); int j = i - 2; c[0] = det(line[5], line[1], line[2], line[3], line[4], i) / d; c[1] = det(line[0], line[5], line[2], line[3], line[4], i) / d; if (j == 0) cout << "m = 1\n" << c[1] << "x+" << c[0] << endl; else { c[2] = det(line[0], line[1], line[5], line[3], line[4], i) / d; j--; if (j == 0) cout << "m = 2\n"<< c[2] << "x^2+" << c[1] << "x+" << c[0] << endl; else { c[3] = det(line[0], line[1], line[2], line[5], line[4], i) / d; j--; if (j == 0) cout << "m = 3\n" << c[3] << "x^3+" << c[2] << "x^2+" << c[1] << "x+" << c[0] << endl; else { c[4] = det(line[0], line[1], line[2], line[3], line[5], i) / d; j--; if (j == 0) cout << "m = 4\n" << c[4] << "x^4+" << c[3] << "x^3+" << c[2] << "x^2+" << c[1] << "x+" << c[0] << endl; } } } } temp = _getch(); } while (temp != 27); return 0; } | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||