Отчет по лабораторным работам по дисциплине Конструирование программ
 Скачать 356.47 Kb. Скачать 356.47 Kb.
|
Лабораторная работа № 7. Вычисление собственных значений (чисел) и векторов матрицК настоящему времени имеется много различных алгоритмов решения проблемы собственных значений. Все они эффективны, но достаточно сложны и трудоемки. К наиболее простым методам нахождения собственных чисел относится степенной метод. К сожалению, им можно определить лишь два максимальных по модулю собственных значения. Также довольно простой метод обратных итераций, очень похожий на степенной по алгоритму, позволяет находить собственный вектор, соответствующий заданному собственному числу. Это итеративный метод, он дает приближение к собственному вектору, сходящееся к нему по направлению. Следует заметить, что при вычислении собственных векторов имеется определенный произвол. Собственные векторы линейного оператора, отвечающие определенному собственному числу, образуют линейное пространство. Различные способы вычисления собственных векторов дают разные базисы этого пространства и, следовательно, разные координаты собственных векторов, удовлетворяющих, однако, основному определению собственного вектора 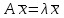 . . Число 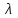 называется собственным значением (собственным числом) матрицы называется собственным значением (собственным числом) матрицы 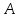 , если существует ненулевой вектор , если существует ненулевой вектор 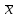 , удовлетворяющий уравнению , удовлетворяющий уравнению 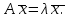 (5.10.1) (5.10.1)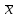 называется собственным вектором матрицы называется собственным вектором матрицы 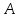 , соответствующим собственному числу , соответствующим собственному числу 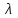 . .Перепишем (5.10.1) в виде 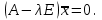 Это однородная система уравнений. Чтобы существовало решение этой системы Это однородная система уравнений. Чтобы существовало решение этой системы 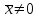 , необходимо чтобы определитель матрицы этой системы был равен нулю, то есть , необходимо чтобы определитель матрицы этой системы был равен нулю, то есть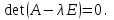 (5.10.2) (5.10.2)Раскрытие этого уравнения приводит к характеристическому уравнению 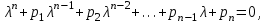 (5.10.3) (5.10.3)Задание № 1. Определить собственные значения и собственные вектора матрицы 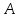 средствами пакета Mathcad, затем найти максимальное по модулю собственное число и соответствующий ему собственный вектор с помощью подпрограмм средствами пакета Mathcad, затем найти максимальное по модулю собственное число и соответствующий ему собственный вектор с помощью подпрограмм 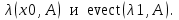 25. 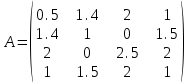 Код программы #include #include using namespace std; int main() { setlocale(LC_ALL, "rus"); const double E = 0.0000001; double A[4][4], x[4], prev, y[4], h[4], temp; for (int i = 0; i < 4; ++i) { cout << "Строка №" << i << endl; for (int j = 0; j < 4; ++j) cin >> A[i][j]; x[i] = 0; } x[0] = 1; for (int k = 0; k < 2; ++k) { do { for (int i = 0; i < 4; ++i) { y[i] = 0; for (int j = 0; j < 4; ++j) y[i] += A[i][j] * x[j]; } prev = h[k]; h[k] = 0; for (int i = 0; i < 4; ++i) h[k] += x[i] * y[i]; temp = 0; for (int i = 0; i < 4; ++i) temp += y[i] * y[i]; temp = sqrt(temp); for (int i = 0; i < 4; ++i) x[i] = y[i] / temp; } while ((h[k] - prev) > 0.001); if (k == 0) for (int i = 0; i < 4; ++i) A[i][i] -= h[0]; else for (int i = 0; i < 4; ++i) A[i][i] += h[0]; } h[1] += h[0]; cout << h[0] << endl << h[1]; _getch(); return 0; } Лабораторная работа № 8. Решение систем нелинейных уравнений методом НьютонаОсновная идея метода Ньютона состоит в выделении из уравнений системы 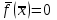 линейных частей, которые являются главными при малых приращениях аргументов. Это позволяет свести одну исходную задачу к решению последовательности задач для линейных систем. линейных частей, которые являются главными при малых приращениях аргументов. Это позволяет свести одну исходную задачу к решению последовательности задач для линейных систем.Итерационная формула метода Ньютона для системы нелинейных уравнений (6.4.7) имеет вид 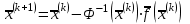 . Необходимость обращения матрицы первых частных производных при каждой итерации сильно затрудняет решение. Эти затруднения чаще носят технический характер, тем не менее вместо уравнения (6.4.7) иногда решают систему линейных алгебраических уравнений вида (6.4.8): . Необходимость обращения матрицы первых частных производных при каждой итерации сильно затрудняет решение. Эти затруднения чаще носят технический характер, тем не менее вместо уравнения (6.4.7) иногда решают систему линейных алгебраических уравнений вида (6.4.8):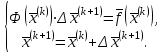 По методу Ньютона итерационный процесс при наличии хорошего начального приближения сходится с квадратичной скоростью, то есть если 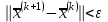 , то , то 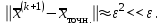 В методе Ньютона применяется линеаризация системы (6.4.1). Пусть по выбранному 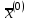 построены приближения построены приближения 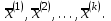 Заменим в системе (6.4.1) каждую из функций Заменим в системе (6.4.1) каждую из функций 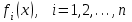 линейной частью ее разложения по формуле Тейлора в точке линейной частью ее разложения по формуле Тейлора в точке 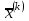 : :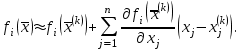 (6.4.2) (6.4.2) В матричной форме система (6.4.3) будет иметь вид 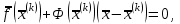 (6.4.4) (6.4.4)где матрица Якоби  (6.4.5) (6.4.5)Задание № 1. Любым способом, разобранным в этой лабораторной работе, решить методом Ньютона следующую систему уравнений: 25. 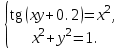 Код программы #include #include using namespace std; double tg(double x) { return x + x*x*x / 3 + 2 * x*x*x*x*x / 15 + 17 * x*x*x*x*x*x*x / 315; } double func1(double x, double y) { return tg(x*y + 0.2) - x*x; } double func2(double x, double y) { return x*x + y*y - 1; } int main() { const double E = 0.001, h = 0.001; double x[2], y[2], prev[2], F[2][2], det, temp; cout << "tg(xy + 0.2) = x^2" << endl << "x^2 + y^2 = 1" << endl; x[0] = 0.1; x[1] = 0.1; do { prev[0] = x[0]; prev[1] = x[1]; F[0][0] = (func1(prev[0] + h, prev[1]) - func1(prev[0] - h, prev[1])) / (2 * h); F[0][1] = (func1(prev[0], prev[1] + h) - func1(prev[0], prev[1] - h)) / (2 * h); F[1][0] = (func2(prev[0] + h, prev[1]) - func2(prev[0] - h, prev[1])) / (2 * h); F[1][1] = (func2(prev[0], prev[1] + h) - func2(prev[0], prev[1] - h)) / (2 * h); det = F[0][0] * F[1][1] - F[0][1] * F[1][0]; temp = F[0][0]; F[0][0] = F[1][1] / det; F[1][1] = temp / det; F[0][1] /= -det; F[1][0] /= -det; y[0] = func1(prev[0], prev[1]); y[1] = func2(prev[0], prev[1]); x[0] = prev[0] - F[0][0] * y[0] - F[0][1] * y[1]; x[1] = prev[1] - F[1][0] * y[0] - F[1][1] * y[1]; } while (((x[0] - prev[0]) > E) || ((x[1] - prev[1]) > E)); cout << "x = " << x[0] << endl << "y = " << x[1] << endl; _getch(); return 0; } |
