Перечень вопросов по тувд
 Скачать 1.76 Mb. Скачать 1.76 Mb.
|
2.Двойственность задач линейного программирования, пример в системе ОрВД.Двойственность задач ЛП сводится к тому, что вместо поиска MAX, можно искать MIN двойственной задачи с другими переменными и наоборот. Св-ва двойственности ЗЛП: 1. В одной задаче находится MAX целевой функции, в другой MIN. 2. Кэффы при переменных в целевой функции одной задачи являются свободными членами систем ограничений другой задачи и наоборот. 3. Число неравенств в системе ограничений одной задачи совпадает с числом неравенств в другой 4. Условия не отрицательности переменных сохраняется в обоих задачах. Для того чтобы во множестве ограничений было однообразие при решении ЗЛП целесообразно привести к одному из двух видов: стандартному (когда все ограничения в виде неравенств с одним знаком) или каноническому (все ограничения есть равенство). БИЛЕТ 51. На чем основано воспроизведение решений в ИМ ОВД.Воспроизведение исследования Имитационной Модели ОВД позволяет установить причины и предпосылки неожиданных результатов, что часто не возможно в реальной системе. Особенности имитационного моделирования заключаются в том, что имитационная модель позволяет воспроизводить моделируемые объекты с сохранением их логической структуры и поведенческих свойств, динамики воздействий. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ – частный случай, при котором изучаемая система заменяется моделью, с достаточной точностью описывает реальную систему, с которой производятся эксперименты с целью получения инфы об этой системе. Имитационное моделирование – метод, позволяющий строить модели, описывающие процессы так, как они протекали бы в действительности. Такую модель можно «проиграть» во времени как для одного испытания, так и заданного их множества. При этом результаты будут определятся случайным характером процессов. По этим данным можно получить достаточно устойчивую статистику. 2. Формализация и обработка неопределённости в представлениях объектов.В представлениях объектов можно выделить неопределенности 2х видов: - неопределенность событий (неопределенность координат события в опорном базисе) - неопределенность отношений между событиями-признаками ситуации и зависимым событием в данном ситуационном базисе. Способы формализации: 1. Нечеткие события и нечеткие преобразования 2. Нечеткие ситуации 3. Нечеткие экземпляры объектов 4. Комбинирование нечетких экземпляров Мышление проявляется при решении задач, когда человек сталкивается с объективной реальностью. Наиболее частый вид - решение задач Механизм - анализ\синтез Оперативная деятельность - оперативное мышление. Выражается в формализации и моделировании с учетом неопределенности (если я сделаю ТАК, то что будет дальше?) БОЛЕЕ ПОДРОБНО Виды неопределенности в представлениях объектов. По времени возникновения неопределённости распределяются на ретроспективные, текущие и перспективные. Необходимость учёта фактора времени при оценке экономической эффективности принимаемых решений обусловлена тем, что как эффект, так и затраты могут быть распределены во времени. Равные по величине затраты, по-разному распределённые во времени, обеспечивают неодинаковый полезный результат того или иного вида (экономический, социальный, политический и т.д.). • По факторам возникновения неопределённости подразделяются на экономические и политические. Эти виды неопределённости тесно связаны между собой, и часто на практике. • Неопределённость внешней среды. При экономическом анализе предпринимательской деятельности вводятся понятия внешней и внутренней среды. Внутренняя среда включает факторы, обусловленные деятельностью самого предпринимателя и его контактами. Внешняя среда представлена факторами, которые не связаны непосредственно с деятельностью предпринимателя и имеют более широкий социальный, демографический, политический, экономический и иной характер. БИЛЕТ 61. Постановка задачи, основные понятия динамического программирования.Суть этого метода состоит в том, что при оптимизации динамических процессов необходимо найти последовательность оптимальных решений Х1, Х2, Х3.., для одного состояния динамического объекта, 2-го, 3-го и т.д., тем самым найти оптимальную траекторию движения объекта из начального в конечное желаемое состояние. Динамическое программирование основано на Принципе Оптимальности Беллмана (каково бы ни было состояние объекта на не- котором, k-м шаге управления, управляющее воздействие на этом шаге нуж- но выбирать так, чтобы затраты на этом шаге плюс затраты на всех последующих шагах были наименьшие по сравнению со всеми другими возможными управляющими воздействиями.) НИЖЕ БОЛЕЕ ПОДРОБНО Алгоритм метода динамического программирования. При оптимизации динамических процессов необходимо определить оптимальную траекторию движения управляемого объекта из первоначального состояния в желаемое и последовательность управляющих воздействий, которая позволяет реализовать эту оптимальную траекторию. В динамическом программировании как и ранее при оптимизации статических процессов состояние объекта описывается вектором X. При этом состояние объекта на первом шаге управления описывается вектором X0; на втором шаге вектором X1; на к-м шаге –X*; конечное состояние, в которое попадает управляемый объект после m-го шага управления – вектором Xm. Считается, что на каждом шаге управления имеется доступное множество управляющих воздействий Uk из которого выбирается то управление ик, которое будет переводить объект в последующее состояние. Этот k-й шаг управления записывается так: 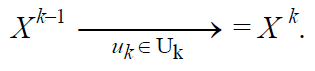 Выбирая различные управляющие воздействия на том или ином шаге управления, в итоге можно получить различные траектории движения объекта из состоянияX0 в состояниеXm. Это значит, что каждой возможной траектории соответствует своя последовательность управляющих воздействий, которая называется также стратегией управления: U=(u1,u2, … uk, …um). Задача состоит в том, чтобы найти такую стратегию управления, которая была бы оптимальной, т.е. соответствовала оптимальной траектории движения объекта. Трудность оптимизации заключается в том, что выбирая в одном состоянии управление, трудно оценивать его оптимальность с точки зрения суммарных затрат на последующих шагах. Иными словами, выбор на k-м шаге управления, которое наименьшее по затратам именно на этом шаге, в итоге может привести в такие состояния на последующих шагах, которые потребуют значительных затрат для вывода объекта в желаемое состояние; наоборот, менее предпочтительное управление на данном шаге может оказаться выгодным в том смысле, что приведет в такие состояния, которые на следующих шагах потребуют минимальных затрат. Чтобы преодолеть эти трудности, метод динамического программирования основывается на использовании так называемого принципа оптимальности (принцип Беллмана). Одна из его формулировок следующая: каково бы ни было состояние объекта на не- котором, k-м шаге управления, управляющее воздействие на этом шаге нуж- но выбирать так, чтобы затраты на этом шаге плюс затраты на всех последующих шагах были наименьшие по сравнению со всеми другими возможными управляющими воздействиями. |
