Перечень вопросов по тувд
 Скачать 1.76 Mb. Скачать 1.76 Mb.
|
2. Форма записи задач линейного программирования и их взаимные преобразования.Чтобы в множестве ограничений было единообразие при решении различных задач линейного программирования, их целесообразно привести к одному из двух видов – стандартному каноническому. Приведение к каноническому виду используется, в частности, при решении ЗЛП симплекс-методом. Стандартный вид: все ограничения записаны в виде неравенства с 1 знаком. Канонический вид: все ограничения -равенства Преобразование одного вида записи в другой, т.е. приведение к одному виду записи всех ограничений, может быть выполнено следующим образом. 1. Стандартный к каноническому - путем введения дополнительных переменных: например, если в ЗЛП с неравенствами типа aj1x1 + aj2x2+ aj3x3 ≤ bj добавить переменную x4 с коэффициентом aj4 =1 (или «–1» в случае «≥»), то можно записать aj1x1 + aj2x2+ aj3x3 + aj4x4 = bj. 2. Канонический к стандартному – путем введения вместо одного равенства двух неравенств: вместо aj1x1 + aj2x2+ aj3x3 + aj4x4 = bj можно записать aj1x1 + aj2x2+ aj3x3 + aj4x4 ≤ bj, aj1x1 + aj2x2+ aj3x3 + aj4x4 ≥ bj. Кроме упомянутых видов записи и их взаимных преобразований можно преобразовать задачу поиска минимума в задачу поиска максимума (или наоборот) путем БИЛЕТ 7 1. Какие подсистемы учитываются при анализе процессов в контуре ОВД В зависимости от решаемых задач.(Сие слово из Крыжановского стр 24.) ЕТО не точно  2. Требования к структурному построению модели в системе ОрВД.Для того чтобы во множестве ограничений было однообразие при решении ЗЛП целесообразно привести к одному из двух видов: стандартному (когда все ограничения в виде неравенств с одним знаком) или каноническому (все ограничения есть равенство). Нужно: а) определение организационных приоритетов и задач; b) определение порядка осуществления деятельности; с) наем, обучение и контроль за деятельностью сотрудников; d) обеспечение оборудованием для деятельности по предоставлению услуг; е) использование навыков персонала; f) распределение необходимых ресурсов БИЛЕТ 815. Наличие каких групп задач характеризуют условия решений по ОВД.Классификация задач ПР: 1. По регулярности проблемной ситуации (новые, уникальные, повторяющ) 2. По длительности периода реализации ( долгосрочные, среднесрочные(тактические), краткосрочные(оперативные))
Задачи, характеризующие условия ПР: 1) Задачи релейного типа, когда диспетчер принимает решение в виде разрешения или запрещения; 2) Задачи траекторного управления; 3) Задачи выбора, когда диспетчеру нужно из множества допустимых альтернативных вариантов выбрать наиболее рациональное. 2. Решения транспортной задачи линейного программирования графическим способом. Задачи о назначениях: особенности и примеры использования при оптимизации процессов ОВД.ТРАНСПОРТНАЯ ЗАДАЧА. Пусть имеется а\д на который пребывают ВС. По причинам (пр. метеоусловия) а/д закрывается. ВС рассредоточены по различным ЗО. Такое может быть если в районе а/д имеется несколько коридоров и в этих коридорах организованы ЗО. Кол-во ЗО  , кол-во ВС в ЗО , кол-во ВС в ЗО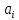 , кол-во запасных а/д , кол-во запасных а/д 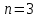 ,кол-во ВС которые может принять запасной а/д ,кол-во ВС которые может принять запасной а/д 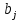 . .Предполагается что все ВС из ЗО могут быть приняты на запасной а/д. Это может быть записано следующим образом  Обозначим  – количество ВС которые отправляются из i ЗО на j а/д. Тогда если мы все ВС должны отправить из ЗО необходимо чтобы выполнялось требование: – количество ВС которые отправляются из i ЗО на j а/д. Тогда если мы все ВС должны отправить из ЗО необходимо чтобы выполнялось требование: 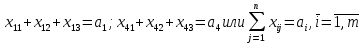 . Все ВС отправленные на запасной а/д должны дойти до а/д назначения: . Все ВС отправленные на запасной а/д должны дойти до а/д назначения:  . Хотя в более общем случае главным . Хотя в более общем случае главным является условие  При формулировке ТЗ, считается что все вероятности принимающих а/д реализованы полностью, поэтому принимается равенство. Критерием оптимизации будем считать затраты к запасному а/д, тогда можем записать математическую формулу ТЗ: При формулировке ТЗ, считается что все вероятности принимающих а/д реализованы полностью, поэтому принимается равенство. Критерием оптимизации будем считать затраты к запасному а/д, тогда можем записать математическую формулу ТЗ:  . Минимизировать . Минимизировать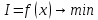 суммарные затраты на передвижение ВС из m ЗО в n запасных а/д. Сумма суммарные затраты на передвижение ВС из m ЗО в n запасных а/д. Сумма  , ,  . . Задача может быть усложнена если на маршруты полета накладывается ограничение по пропускной способности тогда добавляются ограничения вида:  . И чтобы ТЗ с ограниченными . И чтобы ТЗ с ограниченными 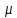 была разрешима необходимо выполнить неравенства: была разрешима необходимо выполнить неравенства:  . Если не выполняется условие: количество находящихся в ЗО ВС меньше чем могут принять запасные а/д, то для решения задачи применяют след. Искусственный прием: вводят ещё один . Если не выполняется условие: количество находящихся в ЗО ВС меньше чем могут принять запасные а/д, то для решения задачи применяют след. Искусственный прием: вводят ещё один  дополнительный пункт ожидания для которого полагают дополнительный пункт ожидания для которого полагают 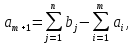 стоимость полета от фиктивной ЗО до каждого запасного а/д принимают равным 0. В результате приходим к стандартной ТЗ. стоимость полета от фиктивной ЗО до каждого запасного а/д принимают равным 0. В результате приходим к стандартной ТЗ.ЗАДАЧА О НАЗНАЧЕНИЯХ. Является частным случаем общей ТЗ. n-самолетов. Требуется установить очередность посадки таким образом чтобы суммарное нахождение ВС в РА было минимальным. Прибывающие ВС находятся в зоне ожидания.  - интервал времени на который должно быть задержано i-е ВС при заходе за j-ым. Если - интервал времени на который должно быть задержано i-е ВС при заходе за j-ым. Если  то будем считать что то будем считать что 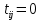 . Введем переменные . Введем переменные . Переменная . Переменная может принимать 2 значения (0;1), причем если i ВС следует за j, то может принимать 2 значения (0;1), причем если i ВС следует за j, то  . В противном случае . В противном случае 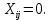 Т.к. можно реализовать один вариант очередности, то соблюдаетсяусловие Т.к. можно реализовать один вариант очередности, то соблюдаетсяусловие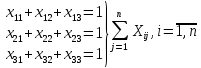 Аналогично 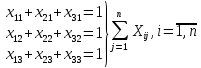 (то есть 1 может следовать только за 1,2,3) (то есть 1 может следовать только за 1,2,3)Таким образом имеем следующую задачу линейного программирования: 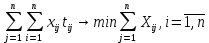 , ,  Как рассчитывается  . Известно, что при заходе на посадку на 4 развороте м/у ВС должно быть не менее одной единицы времени. Но надо учесть, что если более скоростное ВС следует за менее скоростным, то необходимо создать дополнительный интервал времени. . Известно, что при заходе на посадку на 4 развороте м/у ВС должно быть не менее одной единицы времени. Но надо учесть, что если более скоростное ВС следует за менее скоростным, то необходимо создать дополнительный интервал времени.  Минимальный интервал между ВС выходящими из ЗО а также между посадками ВС равен 1 и совокупный интервал будет следующим:  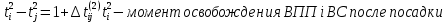 |
