Перечень вопросов по тувд
 Скачать 1.76 Mb. Скачать 1.76 Mb.
|
БИЛЕТ 161. Классификация по решаемым задачам и алгоритмы функционирования СППР.СППР - компьютерная автоматизированная система, целью которой является помощь людям, принимающим решение в сложных условиях для полного и объективного анализа предметной деятельности. - Пассивная СППР - система, которая помогает процессу принятия решения, но не может вынести предложение, какое решение принять. - Активная СППР может сделать предложение, какое решение следует выбрать. - Кооперативная позволяет ЛПР изменять, пополнять или улучшать решения, предлагаемые системой, посылая затем эти изменения в систему для проверки. Система изменяет, пополняет или улучшает эти решения и посылает их опять пользователю. Процесс продолжается до получения согласованного решения. 2.Формы записи задачи линейного программирования в их взаимные преобразования.(ПОВТОР) БИЛЕТ 171. Алгоритм построения универсальной модели, отражающей совокупность всех свойств объекта.Основные этапы построения модели. 1) Выделение системы из внешней среды. Наблюдение за системой, накопление информации, достаточной для выдвижения гипотез о структуре системы и ее функционировании. 2) Выбор аппарата формализации. Осуществляется исследователем и зависит от целей моделирования, имеющейся информации, полученных экспериментальных данных. 3) Построение внешнего описания. Сводится к поиску области определения и области значений, определении соответствия между входными и выходными параметрами. 4) Проверка адекватности показывает, что если построенная модель не удовлетворяет предъявляемым к ней требованиям и причиной этого является более сложная система, то производится выбор нового метода математического описания. 5) Построение внутреннего описания. производится переход от внешнего к внутреннему описанию. При этом размерность пространства состояний системы должна быть минимальной. 6) Определение параметров, определяющих функционирование системы. ОБЩАЯ СХЕМА МОДЕЛИРОВАНИЯ 1) Изучение и анализ реального объекта 2) определение цели исследования 3) Содержательное описание модели 4) Построение формализованной схемы 6) Оценка модели 7) Планирование экспериментов 8) Экспериментирование 9) Обработка результатов 10) Использование полученных данных 2. Стохастическая оптимизация статических процессов.Стохастическая оптимизация — класс алгоритмов оптимизации, использующая случайность в процессе поиска оптимума. Случайность может проявляться в разных вещах. Алгоритмы стохастической оптимизации используются в случае, если целевая функция сложная, многоэкстремальная, с разрывами, с помехами и пр. МЕТОДЫ ОПТИМИЗАЦИИ СМОТРИ ЗДЕСЬ БИЛЕТ 181. Динамическая загрузка и модель диспетчера.МОДЕЛЬ ДИСПЕТЧЕРА - совокупность правил и технологий, а также алгоритм формирования и реализации решений по ОВД. В этой модели путем сложных соответствующих затрат времени на выполнение операций по ОВД должна определяться и учитываться динамическая загрузка на диспетчера, с ее учетом должны формироваться и вводиться ошибки при ОВД. Динамическая загрузка — общее количество ВС, одновременно находящихся на связи СВЯЗЬ ЧЕМ БОЛЬШЕ У ТЕБЯ ВОЗДУШНЫХ СУДОВ НА УПРАВЛЕНИИ ТЕМ БОЛЬШЕ ВРЕМЕНИ ТЫ ТРАТИШЬ. 2. По каким признакам классифицируются регулирования движения ВС.1) По отношению к рассматриваемой системе: внутренняя и внешняя 2) По степени непрерывности: непрерывная и дискретная 3) По степени регулярности: детерминированные и стохастические 4) По степени стабильности: постоянные и нестабильные 5) По степени изменчивости: стационарные и нестационарные 6) По характеру перемещения движения: равномерные и неравномерные 7) По степени периодичности: периодические и непериодические 8) По степени сложности: простые, дифференцированные (одни объекты) и сложные (разные объекты) 9) По степени управляемости: управляемые и неуправляемые БИЛЕТ 191. Чему равно среднее число заявок системе.Среднее число заявок в системе равно произведению интенсивности входного потока на среднее время пребывания заявки в системе. Одноканальная система с неограниченной очередью. На практике часто встречаются одноканальные СМО с неограниченной очередью (например, определенный канал авиадиспетчера). Рассмотрим задачу. Имеется одноканальная СМО с очередью, на которую не наложены никакие ограничения (ни по длине очереди, ни по времени ожидания). Поток заявок, поступающих в СМО, имеет интенсивность λ, а поток обслуживании — интенсивность μ. Необходимо найти предельные вероятности состояний и показатели эффективности СМО. Пропускная способность-величина, обратная времени обслуживания Предельная вероятность состояний-это вероятность максимальной очереди Система может находиться в одном из состояний S0, S1, S2, …, Sk, по числу заявок, находящихся в СМО: S0 — канал свободен; S1 — канал занят (обслуживает заявку), очереди нет, S2 — канал занят, одна заявка стоит в очереди; ... Sk — канал занят, (k—1) заявок стоят в очереди и т.д. Граф состояний СМО представлен на рис.  Это процесс гибели и размножения, но с бесконечным числом состояний, в котором интенсивность потока заявок равна λ, а интенсивность потока обслуживании μ. Прежде чем записать формулы предельных вероятностей, необходимо быть уверенным в их существовании, ведь в случае, когда время t→∞, очередь может неограниченно возрастать. Доказано, что если ρ<1, т.е. среднее число приходящих заявок меньше среднего числа обслуженных заявок (в единицу времени), то предельные вероятности существуют. Если ρ≥1, очередь растет до бесконечности. По другому р-это отношение интенсивности к пропускной способности. Формула среднего числа заявок: L = 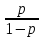 То есть интенсивность самолетов в час=4, максимально может быть обслужено 5 ВС в час. Р=4/5=0.8 Среднее число заявок в системе:L=0.8/0.2=4 ВС |
