Риски. Практика 4 Риски. Показатели измерения риска и методы его оценки

• Название: Показатели измерения риска и методы его оценки
• Анкор: Риски
• Дата: 24.03.2022
• Размер: 4.17 Mb.
• Имя файла: Практика 4 Риски.doc
• Тип: Документы; #413219
• страница: 1 из 20

Показатели измерения риска и методы его оценки

Случайным называется событие, которое при данном комплексе условий может произойти либо не произойти.

Под вероятностью Р события Е понимают отношение числа К случаев, благоприятствующих наступлению этого события, к общему числу M всех равновозможных случаев.

Свойства:

• 
  вероятность события есть число неотрицательное;
  
• 
  вероятность достоверного события, т. е. события, которое при данном комплексе условий непременно произойдет, равна 1; вероятность невозможного события равна 0;
  
• 
  вероятность события может принимать значения, лежащие в диапазоне от 0 до 1.
  

Большинство случайных явлений, происходящих в жизни, характеризуются наличием большого числа случайных факторов. Их можно описать законом нормального распределения, который является основным во многих практических исследованиях. Нормальное распределение вероятности Гаусса¹ характеризуется двумя параметрами, которые являются основными критериями измерения риска:

1. 
   средним ожидаемым значением;
   
2. 
   среднеквадратическим отклонением, или степенью риска, определяющим колеблемость (изменчивость) возможного результата.
   

Математическое ожидание служит центром распределения вероятностей. Среднее ожидаемое значение измеряет результат, который мы ожидаем в среднем. Для равной вероятности наступления событий (т.е. при р_k=1/n):



Стандартное или среднеквадратическое отклонение - характеристика разброса (вариации) случайной величины от ее центра распределения (среднего значения м(е)), рассчитывается, как корень из дисперсии - суммы квадратов отклонений случайной величины от ее среднего значения, взвешенных на соответствующие вероятности.



Риск имеет математически выраженную вероятность наступления потери. Вероятность означает возможность получения определенного результата. Под вероятностью р события Х понимают отношение числа К случаев, благоприятствующих наступлению этого события, к общему числу М всех равновозможных событий. Свойства вероятности: р(Х)>=0, вероятность достоверного события =1, невозможного =0: 0>=р(Х)>=1. Сумма вероятностей должна быть:



Любое правило, позволяющее находить вероятности всех значений случайной величины Х, называют законом распределения ее вероятностей. Случайная величина имеет нормальное распределение вероятностей с параметрами а (а=М(x)) и s, если плотность ее распределения задается формулой: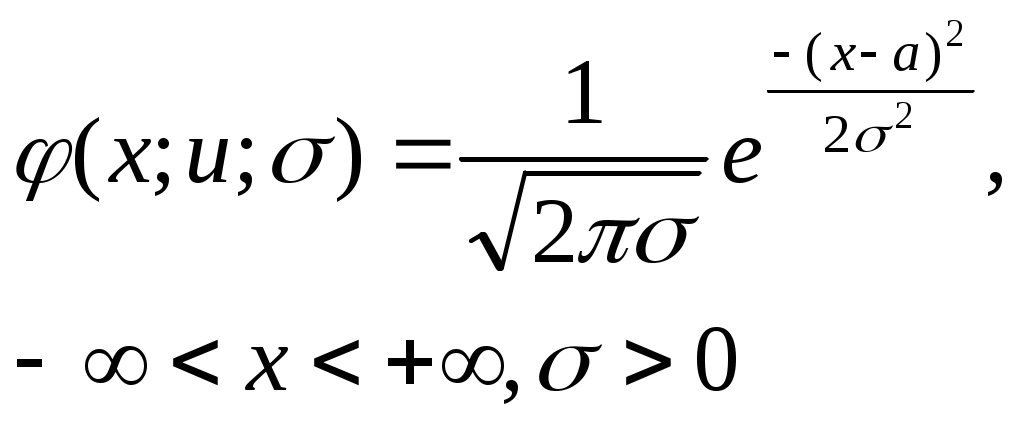



При этом среднеквадратическое отклонение характеризует форму кривой распределения. С увеличением значения кривая распределения «растягивается» вдоль оси абсцисс.

На графике уравнение, описывающие плотность вероятности нормального распределения, представляет собой симметричную кривую Гаусса, имеющую максимум в точке соответствующей значению Х = М (соответствует среднему арифметическому Х_ср и называется центром группирования).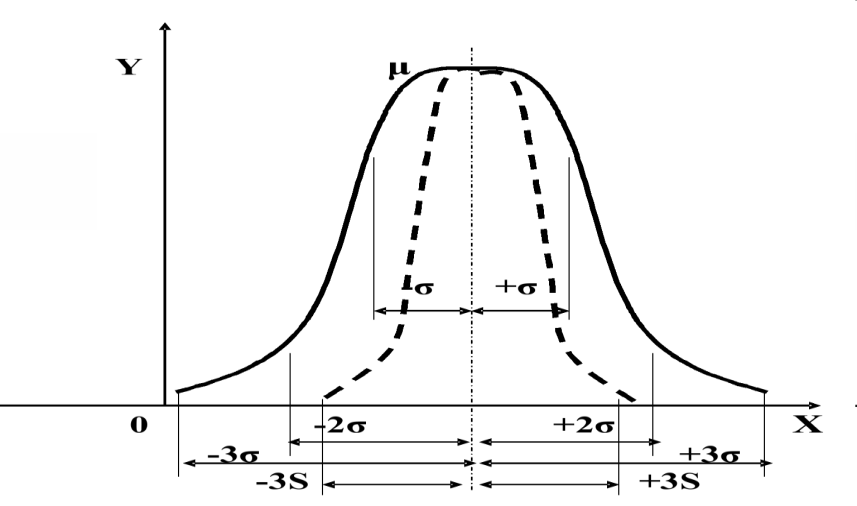


М ± 


Рисунок 1. График функции плотности нормального распределения вероятности

В интервале М ±  расположено 68,3% всей площади кривой. Это означает, что при нормальном распределении 68,3 % всех измеренных единиц отклоняются от среднего значения не более чем на σ. А значит ожидаемое значение Х лежит в интервале: (М - ) < Х< (М + ).

Нормальное распределение не является единственно возможным. В зависимости от физической природы случайных величин, некоторые из них на практике могут иметь распределение другого вида, например, логарифмическое, экспоненциальное, Вейбулла, Симпсона, Релея, равной вероятности и др. Для характеристики формы распределения обычно используют ту математическую модель, которая наилучшим образом приближает к виду кривой распределения вероятностей, полученной при анализе экспериментально полученных данных.

К оэффициент вариации - это относительный показатель, определяющий степень риска на единицу среднего дохода:

К оэффициент ассиметрии (скоса - skew) - нормированная величина третьего центрального момента:

Для нормального распределения величина скоса s=0: M(x)±d.

Если S>0, самые высокие доходы (правый «хвост») считаются более вероятными, чем самые низкие: M(x)+d.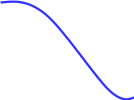



Рисунок 2. Правосторонний скос – получение более высоких доходов вероятнее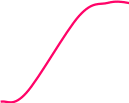



Рисунок 3. Левосторонний скос – получение низких доходов вероятнее

Если S<0, низкие доходы (левый «хвост») считаются более вероятными, чем высокие: M(x)-d.

Эксцесс – excess - четвертый нормированный центральный момент: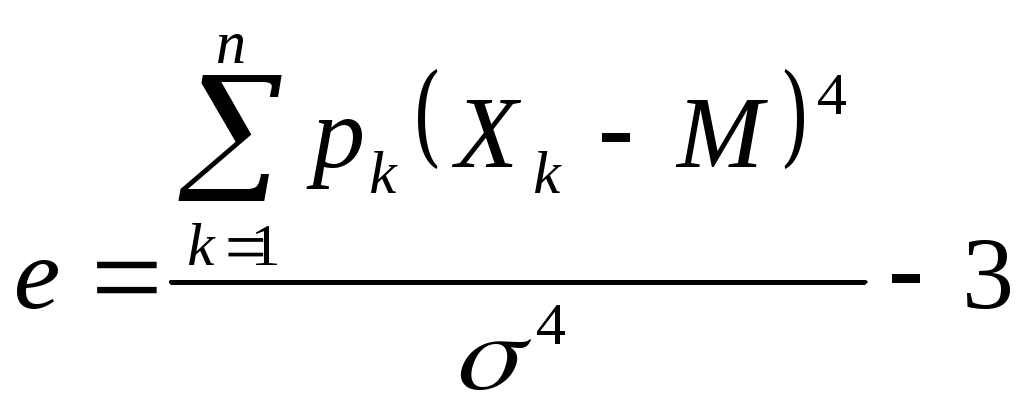



Для нормального распределения величина эксцесса е=0: M(x)±d.

Е 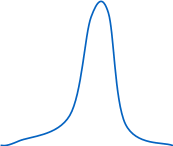сли е>0, кривая распределения более остроконечна, чем нормальная кривая: M(x).



Рисунок 4. Положительный эксцесс – получение доходов ближе к среднему их значению вероятнее

Если е<0, кривая распределения более полога, чем нормальная кривая: M(x)±d



Рисунок 5. Отрицательный эксцесс – получение доходов ближе к значению с учетом отклонения вероятнее