Риски. Практика 4 Риски. Показатели измерения риска и методы его оценки

• Название: Показатели измерения риска и методы его оценки
• Анкор: Риски
• Дата: 24.03.2022
• Размер: 4.17 Mb.
• Имя файла: Практика 4 Риски.doc
• Тип: Документы; #413219
• страница: 3 из 20

Кейс: расчет рисков проектов

Кейс 1. Анализ рисков акций «Н»

Рассматривается возможность покупки акций недавно образованной фирмы «Н». Предполагается, что прогнозируемая доходность по акциям через год будет зависеть от состояния спроса на продукцию фирмы в течение данного периода и соответственно равна: 12% - повышенный спрос, 9% - обычный спрос, 6% - умеренный спрос.

В приведенном примере предполагается, что доходность акции зависит от реализации одного из трех внешних событий (состояний спроса), каждое из которых имеет равные шансы осуществиться. Так как наступление одного из них исключает наступление двух других (т.е. они попарно несовместимы и равновозможные), вероятность осуществления каждого из них равна 1/3, или 0,33 (33%).

Поскольку на момент принятия решения неизвестно, какое именно из событий произойдет (каким спросом будет пользоваться продукция фирмы в течение года с момента приобретения акций) и принимающий решение не может оказывать никакого влияния на ход событий, можно полагать, что конкретное значение доходности по акциям фирмы за период хранения зависит от случая, т.е. является случайной величиной.

Любое правило, позволяющее находить вероятности всех значений случайной величины Е, называют законом распределения ее вероятностей. Для дискретной случайной величины этот закон задается в виде таблицы, в которой перечисляют все ее возможные значения и их вероятности. При этом если число ее значений конечно, сумма их вероятностей равна 1. Закон распределения вероятностей для рассматриваемого примера приведен в табл.

Событие	Доходность,%	Вероятность
повышенный спрос	12	0,33
обычный спрос	9	0,33
умеренный спрос	6	0,33

Средним, или ожидаемым, значением (математическим ожиданием) дискретной случайной величины Е называется сумма произведений ее значений на их вероятности. Смысл этой характеристики для рассматриваемого примера заключается в том, что она представляет собой наиболее правдоподобную меру годовой доходности по акциям фирмы "Н".

Дисперсией называется сумма квадратов отклонений случайной величины от ее среднего значения, взвешенных на соответствующие вероятности. Дисперсия может служить мерой риска финансовых операций.

В качестве меры разброса случайной величины удобно использовать стандартное (среднее квадратическое) отклонение. Будучи выражено в тех же единицах, стандартное отклонение показывает, насколько значения случайной величины могут отличаться от ее среднего.

Зная закон распределения вероятностей и его основные параметры, можно делать выводы о степени риска проводимой операции. Однако следует всегда помнить о том, что эти выводы будут также носить вероятностный характер.

Еще одним показателем, применяемым при анализе рисков, является коэффициент вариации.

В отличие от стандартного отклонения коэффициент вариации - относительный показатель, он определяет степень риска на единицу среднего дохода. В случае одинаковых или нулевых средних значений доходности вычисление этого показателя теряет смысл. Очевидно, что при равных средних чем больше величина стандартного отклонения о, тем больше коэффициент вариации.

Помимо среднего значения и стандартного отклонения, асимметричные распределения часто требуют знания дополнительного параметра - коэффициента асимметрии (скоса).

Смысл коэффициента асимметрии применительно к рассматриваемой проблеме заключается в следующем. В случае положительного значения коэффициента (положительного скоса) самые высокие доходы (правый "хвост") считаются более вероятными, чем самые низкие. Соответственно в случае отрицательного коэффициента асимметрии более вероятными будут считаться самые низкие доходы. Коэффициент асимметрии может также использоваться для приблизительной проверки гипотезы о нормальном распределении случайной величины. Его значение в этом случае должно быть равным 0.

Для автоматизации расчетов, связанных с нормальным распределением вероятностей, в EXСEL реализован ряд специальных функций. Мы будем использовать две функции - НОРМРАСП и НОРМОБР.

Событие / Функции в MS Excel	Доход, рубль		Вероятность
повышенный спрос	12		0,33
обычный спрос	9		0,33
умеренный спрос	6		0,33
СрЗнач()	М(Е)= =0,33*12+0,33*9+0,33*6=9
Диспр()	VAR(E)=0.33*(12-9)2+0.33*(9-9)2+0.33*(6-9)2=6
СтандОтклонП()	6 = 2,44949
Коэффициент вариации, CV	0,272151918
Интервал: М(Е)-  Е  М(Е)+	9-2,45=6,55  Е  9+2,45=11,45
Скос()	s=(0.33*(12-9)3+0.33*(9-9)3+0.33*(6-9)3) / 2,453 = -2,33147E-15
Эксцесс()	e=(0.33*(12-9)4+0.33*(9-9)4+0.33*(6-9)4) / 2,454 – 3 = -1,499849985
Смещение интервала:	Т.к. s= 0, подтверждается гипотеза о нормальном распределении вероятностей: [М(Е)-; М(Е)+]: 9-2,45=6,55  Е  9+2,45=11,45
	Т.к. e=0, подтверждается гипотеза о нормальном распределении вероятностей
	Е>=6,55	Е<=11.45
Вероятность результата
р(6.5 Е 11.5) Нормрасп()	0,15865526	0,84134474
М(Е)-2  Е  М(Е)+2	9-2*2,45=4,1  Е  9+2*2,45=13,9
	Е>=4,1	Е<=13,9
р(4 Е 14) Нормрасп()	0,022750062	0,977249938
М(Е)-3  Е  М(Е)+3	9-3*2,45=1,65  Е  9+3*2,45=16,35
	Е>=1,65	Е<=16,35
р(1,5 Е 16,5) Нормрасп()	0,001349967	0,998650033

Анализ рисков акций «Н»

СПРОС	Покупка акций компании
	Ожидаемые значения	Вероятность дохода	для 	для скоса - skew	для эксцесс - excecc
	Ei	Pi	Pi *(Ei -M)^2	(Pi *(Ei -M)^3)/ ^3	((Pi *(Ei -M)^4))/ ^4) - 3
повышенный	12	33%	2,9997	0,612403057	0,750075008
обычный	9	33%	1,05202E-30	-1,27173E-46	9,22297E-62
умеренный	6	33%	2,9997	-0,612403057	0,750075008
Среднее ожидаемое значение, M(Ei)	9,00		5,9994
Стандартное среднеквадратичное отклонение, 			2,449367265
Коэффициент вариации, CV			0,272151918
СКОС, s				-2,33147E-15
ЭКСЦЕСС, e					-1,499849985

	M - 	М	M + 		CV	s	e
Н	6,55	9	11,45	2,449	0,272151918	-2,33147E-15	-1,499849985
				 < M	27 копеек возможных потерь на каждый ожидаемый в среднем рубль	s<0 x [M -  M	e<0 x M - 

Ожидаемый результат: значения попадут в интервал x [6,55;9], причем получение низкий доходов вероятнее (е<0).
Для графика функции плотности распределения вероятностей:

max	min	Шаг T=(max+min)/15
12	6	1,2

№№	Точки на графике Хi	ряд Н =НОРМРАСП(Хi;М;;0)
1	1,651898204	0,001809385	= M -3*
2	2,851898204	0,006977860	= Хi +T
3	4,051898204	0,021167642
4	5,251898204	0,050510489
5	6,451898204	0,094809000
6	7,651898204	0,139983375
7	8,851898204	0,162578179
8	10,0518982	0,148527527
9	11,2518982	0,106735907
10	12,4518982	0,060335517
11	13,6518982	0,026828379
12	14,8518982	0,009383713
13	16,0518982	0,002581748
14	17,2518982	0,000558743
15	18,4518982	0,000095119

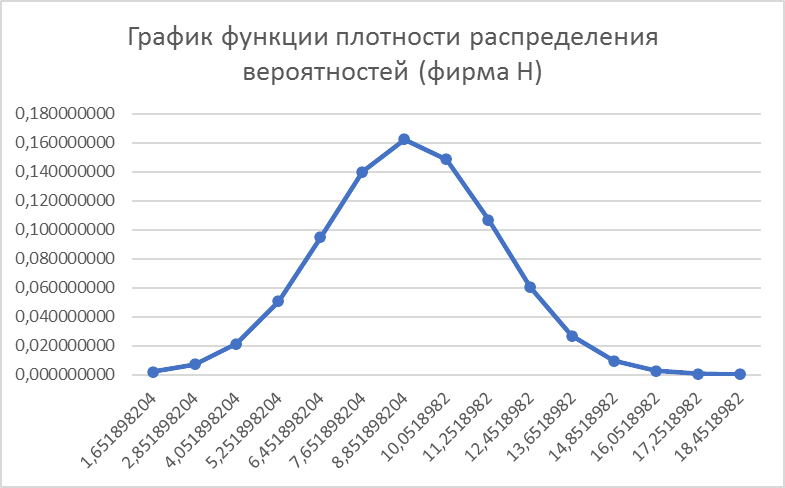Правило трех сигм:

k	(M - k*	М	(M + k*	Вероятность попадание в интервал Р (M - k* <= M <= M+ k*)
1	6,55	9,00	11,45	0,047024205
2	4,10	9,00	13,90	0,627629555
3	1,65	9,00	16,35	0,989979561

=НОРМРАСП((M + k* - (M - k*; М;;1)