Пояснительная записка Цель данного пособия помочь студентам глубже разобраться в разделах теоретической механики Кинематика
 Скачать 1.98 Mb. Скачать 1.98 Mb.
|
|
Работа и мощность. Работа постоянной силы на прямолинейном пути. Произведение модуля силы Р на длину пути s пройденного точкой приложения этой силы, и косинуса угла между направлениями силы Р и скороститочки называют работой, обозначаемой А, т. е. А= P s cos (P,v) В зависимости от угла (Р, v) = α различают следующие случаи: 1. Если 0<α< π/2 , то силы называют движущими. Движущие силы направлены в сторону движения.. При этом О < cos a < 1 и А = P s cos α >0. Работа движущих сил всегда положительна. В частном случае cos = 1 при α = 0, А = P s 2. Направление силы перпендикулярно направлению движения. При этом α= π/2 ; cosα = 0 и А=0 3. Если, π/2 <α< π, то силы называют силами сопротивления. Они направлены против движения. При этом - 1 < cos α А= P s cos α < О. Работа сил сопротивления всегда отрицательна. В частном случае cos α = - 1 при α = π ; А= - P s. В системе (СИ) работа измеряется в джоулях (дж) : 1 дж = 1 Н* 1 м Работа переменной силы на криволинейном пути. В общем случае, когда сила переменная и путь криволинейный, работу определяют по формуле А = Работа равнодействующей. Если на некотором перемещении работу совершает система сил (Р1, Р2, …Рп), то алгебраическая сумма работы этих сил равна работе равнодействующей R на этом же перемещении, т. е. АR = ΣАРi Работа сил тяжести Работа сил тяжести не зависит от формы траектории и равна произведению силы тяжести G на разность начальной h1 и конечной h2 высот, т. е. A = G(h1 — h2). Если начальная высота расположена выше h1> h2, то работа силы тяжести положительна; если конечная высота выше h1< h2, то работа силы тяжести отрицательна; если начальная и конечная высоты находятся на одном уровне h1= h2, то работа силы тяжести равна нулю. Работа при скольжении тела по негладкой наклонной плоскости На тело, скользящее по негладкой наклонной (рис.12), действуют следующие силы: G— вес тела; Т —движущая сила; Fтр — сила трения скольжения; N — нормальная реакция поверхности (рис.13). Полная работа этих сил на перемещении L равна ΣА = АG+АT+АN+АFтр При этом сила тяжести совершает положительную или отрицательную работу (в зависимости от того, опускается тело или поднимается) АG = ± Gh = ± Gl sin a. Движущая сила совершает положительную работу. Нормальная реакция работы не производит АN=0 Сила трения совершает отрицательную работу АFтр = — Fтр l = - ƒ N l= - ƒ (G cos α — Т sin β)l . Таким образом, ΣА = [Т cos β ± G sin α — ƒ (G cos α— Т sin β)] Движение вверх по наклонной плоскости (рис.13,а) 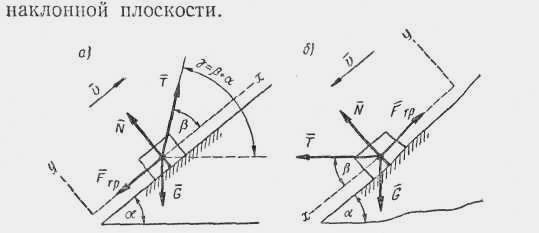 Рис.13 В этом случае сила веса G совершает отрицательную работу. а) Полная работа положительна ΣА >0 (работа движущей силы Т больше работы сил сопротивления Fтр и G — движение равноускоренное). Тогда Т> G (sin α + ƒcos α ) / (cos β +ƒsin β) При этом, если тяговое усилие Т направлено вдоль наклонной (β = 0), то T>G(sinα+ƒcos α) Если тяговое усилие горизонтально (β= —α), то Т> G (sin α + ƒcos α ) / (cos α - ƒsin α) б) Полная работа равна нулю ΣА = 0 (работа движущей силы равна работе сил сопротивления — движение тела с постоянной скоростью, либо тело находится на грани между покоем и движением). Тогда Т= G (sin α + ƒcos α ) / (cos β + ƒsin β) в) Полная работа отрицательна ΣА <0 (работа движущей силы меньше работы сил сопротивления — движение равнозамедленное). Тогда Т< G (sin α + ƒcos α ) / (cos β + ƒsin β) Движение вниз по наклонной плоскости (Рис.13,б) В этом случае вес G совершает положительную работу. а) ΣА >0 —движение ускоренное. Тогда Т> G ( - sin α + ƒcos α ) / (cos β + ƒsin β) при β = 0 Т> G ( - sin α + ƒcos α ) при β = α Т > G ( - sin α + ƒ cos α)/ (cos α + ƒsin α) б) ΣА = 0 — движение равномерное, либо тело находится на грани между движением и покоем. Тогда Т= G ( - sin α + ƒcos α ) / (cos β + ƒsin β) в) ΣА < 0 —движение замедленное. Т > G ( - sin α + ƒ cos α)/ (cos α + ƒsin α) Самоторможение. При движении вниз движущей силой является не только сила тяги, но и вес. Поэтому движение возможно и без приложения силы тяги под действием собственного веса. При этом если угол трения φ больше угла наклонной плоскости α, тело не двигается вниз, а если оно имеет первоначальную скорость, то оно тормозится. Это явление называют самоторможением. Очевидно, при φ = α тело равномерно скользит вниз по наклонной плоскости, при φ<α — ускоренно. Работа сил при вращательном движении твердого тела Работа постоянной силы Р, приложенной к телу, вращающемуся вокруг неподвижной оси Z, равна произведению момента этой силы Mz относительно оси вращения поворота тела, т.е. А = Phφ=Mzφ, где h—плечо силы, относительно оси вращения. При действии переменного момента работу на конечном угловом перемещении φ определяют по формуле А =∫ Mz dφ Работа при вращательном движении твердого тела вокруг неподвижной оси z равна работе суммы моментов всех сил, приложенных к телу, относительно этой оси, А=ΣMz φ При этом тело вращается ускоренно, если А=ΣMz φ>0 Тело вращается с постоянной скоростью, если А=ΣMz φ=0 Тело вращается замедленно, если А=ΣMz φ<0 Мощность. Золотое правило механики Величину работы, совершаемую в единицу времени, называют мощностью. Если работа, производимая машиной в равные промежутки времени, не одинакова, то мощность является переменной величиной. В таких случаях вводят понятие средней мощности, равное отношению всей работы А к промежутку времени Δt, за который она совершена Мощность в данный момент равна первой производной от работы по времени: Мощность силы Р при поступательном движении твердого тела равна произведению модуля силы на модуль скорости и косинус угла между направлениями силы и скорости: N = PV cos (P, v), Мощность момента силы М при вращательном движении твердого тела равна произведению величины момента на угловую скорость вращения: Nм = Mω Мощность имеет размерность дж/сек. Определение мощности по крутящему моменту. В расчетах для определения мощности по крутящему моменту применяют зависимость Mкр = 9560 N/n, где N выражено в кВт, а n — в об/ мин Движущие силы, силы полезных и вредных сопротивлений. При работе к машине приложены: 1. Движущие силы — силы, которые приводят машину в движение. Работа движущих сил всегда положительна, поскольку направление их всегда совпадает с направлением движения. 2. Силы полезных сопротивлений — силы, для преодоления работы которых и создана машина. Работа сил полезных сопротивлений всегда отрицательна, так как машина совершает работу против сил полезного сопротивления. 3. Силы вредных сопротивлений — силы, появляющиеся в механизмах машины вследствие ее несовершенства (силы трения, сопротивления среды и т. д.). Работа сил вредных сопротивлений всегда отрицательна, так как они направлены против движения. Золотое правило механики. В идеальных машинах и механизмах силы вредных сопротивлений отсутствуют, поэтому мощность движущих сил равна мощности сил полезного сопротивления: Nдв.=Nп Пусть к механизму приложены две силы: движущая Р и сила полезного сопротивления Q. Соответственно проекции скоростей точек приложения сил Р и Q на направления самих сил равны Vp и VQ. Тогда Nдв. = PVP и Nn=QVQ или по Nдв.=Nп ; PVP = QVQ. Это равенство называют золотым правилом механики. Его формулируют так: сколько выигрываем в силе, столько теряем в скорости, и наоборот. Золотое правило можно выразить через перемещения: сколько выигрываем в силе, столько теряем в перемещении. В идеальном механизме работа движущих сил за любой промежуток времени равна работе сил полезного сопротивления: Ад=Ап; тогда PSp = QSQ, где Sp и Sq — проекции перемещений точек приложения сил Р и Q на направления самих сил. Золотое правило механики позволяет находить зависимость между движущей силой Р и полезным сопротивлением Q для любого идеального механизма. В реальном механизме всегда присутствуют силы вредного сопротивления, поэтому выигрыш в силе всегда меньше величины, получаемой по золотому правилу механики: Тест №15 Работа и мощность Hf,jnf/ Vjoyjcnm Вопросы группы А Что называется механической работой? Совершается ли механическая работа, если на движущееся тело действуют взаимно уравновешивающиеся силы? Совершается ли работа, если при действии силы на тело оно не перемещается? Какой вид имеет формула работы, когда направление силы совпадает с направлением пути? Какой вид имеет формула работы, когда сила направлена под углом к направлению пути? Что принимается за единицу работы в СИ? Какой вид имеет формула работы, совершаемой под действием силы тяжести? Какой формулой устанавливается связь между мощностью и скоростью равномерного движения? Вопросы группы В Какова размерность работы в СИ? Какое существует соотношение между килограммометром и Джоулем? В каком случае работа является отрицательной? Что называется работой в широком смысле этого слова? Совершается ли работа при свободном падении тел? Совершается ли работа в процессе вращения Земли вокруг Солнца? Что называется мощностью?
Коэффициент полезного действия. Коэффициентом полезного действия (к. п. д.) машины называют отношение работы сил полезного сопротивления Ап к работе движущих сил АД, т. е. ŋ= Ап/ АД К. п. д. характеризует степень совершенства машины. Чем меньше работа сил вредного сопротивления А3, тем выше к. п. д. Коэффициентом полезного действия механизма называют отношение работы, отводимой от механизма, к работе, подводимой к нему. Подводимая работа является работой движущих сил, а отводимая — работой сил полезного сопротивления. Так как мощность — это работа в единицу времени, то к. п. д. равен отношению мощности сил полезного сопротивления Nn к мощности движущих сил Ад, т. е. ŋ= Nп/ NД Последовательное и параллельное соединения механизмов и машин. Механизмы и машины могут быть соединены между собой последовательно и параллельно. Последовательным называют соединение, при котором полезное сопротивление предыдущего элемента является движущей силой для последующего. Коэффициент полезного действия машины (механизма), состоящей из последовательно соединенных элементов, равен произведению к. п. д. этих элементов: ŋ= ŋ1 ŋ2 ŋ3 …. ŋ n Параллельным называют соединение, при котором полезные сопротивления и движущие силы составляющих элементов не зависят друг от друга. Пусть полная работа движущих сил распределяется между элементами следующим образом: Ад = Ад1+ Ад2 + …+Адn Тогда полная работа сил полезного сопротивления Ап = Ад1 ŋ1+ Ад2 ŋ2+ …+Адn ŋn и общий коэффициент полезного действия равен ŋ0= Σ Адi ŋi/ Адi Теоремы динамики 1. Теорема об изменении количества движения материальной точки Произведение массы точки m на скорость V, которой она обладает в данный момент, называют количеством движения материальной точки. Произведение силы Р на время Δt, в течение которого она действует, называют импульсом силы. Теорема об изменении количества движения материальной точки при действии постоянных сил формулируется следующим образом: изменение количества движения материальной точки под действием постоянных сил равно импульсу силы за этот же промежуток времени, т. е. mvK-mv0=ΣP Δt Проектируя это векторное равенство на оси координат, получаем три скалярных равенства: m 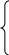 vKx — mv0x = ΣX Δt vKx — mv0x = ΣX ΔtmvKy — mv0y = ΣY Δt mvKz — mv0z = ΣZ Δt Количество движения и импульс силы в системе (СИ) имеют размерность: [mv]=м*кг*сек-1 [Pt]=H сек=м*кг*сек-1 Если импульс сил ΣP Δt за некоторый промежуток времени равен нулю, то скорость постоянна: Vk= V0= const Если проекция импульса сил на какую-нибудь ось равна нулю ΣX Δt=0, то проекция скорости на эту ось постоянна VkхV0х= const |
