Пояснительная записка Цель данного пособия помочь студентам глубже разобраться в разделах теоретической механики Кинематика
 Скачать 1.98 Mb.
|
|
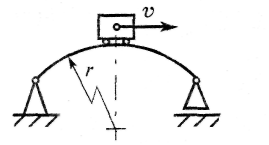
Применение принципа Даламбера при решении задач Приступая к решению задач, в которых рассматривается несвободная материальная точка, нужно, прежде всего, выявить действующие на точку активные силы (движущие силы и силы сопротивления), а также реакции связей (пассивные силы). Выявив действующие силы, необходимо определить, находятся они в равновесии или нет? Этот вопрос в зависимости от заданных условий решается двояко. Если, например, известно, что точка движется равномерно и прямолинейно, значит, система сил уравновешена; если же известно, что точка двигается неравномерно или имеет криволинейную траекторию, то система сил неуравновешенна. Если система сил задана (все силы системы известны), то, определив проекции сил на оси координат, можно установить равновесие или неравновесие системы. В случае, когда суммы проекций всех сил на каждую из осей равны нулю, заданная система сил уравновешена; когда же сумма проекций всех сил хотя бы на одну из осей не равна нулю, система сил неуравновешенна; в первом случае точка движется равномерно и прямолинейно, во втором случае - имеет ускорение (вторая задача динамики). При решении различных технических задач особенно важное значение приобретает случай, когда на материальную точку действует неуравновешенная система сил. В подобных случаях целесообразно решать задачи, применяя так называемый метод кинетостатики или принцип Даламбера, который формулируется так: Активные силы, реакции связей и сила инерции образуют уравновешенную систему сил. Применяя принцип Даламбера, необходимо очень хорошо понимать сущность силы инерции. Нужно помнить, во-первых, что сила инерции, численно равная произведению массы точки на приобретенное ускорение, всегда направлена в сторону, противоположную вектору ускорения; во-вторых, что сила инерции в действительности не приложена к рассматриваемой в задаче материальной точке; она условно прикладывается к этой точке; фактически сила инерции приложена к двигающему телу или к связи; в-третьих, что равновесие сил, которое образуется после добавления силы инерции к силам, приложенным к точке,- равновесие фиктивное; но оно позволяет воспользоваться для решения задачи уравнениями равновесия из статики. При решении задач с применением метода кинетостатики рекомендуется придерживаться такой последовательности: 1. Выделить точку, движение которой рассматривается, и изобразить ее на рисунке; 2. Выявить все активные силы и изобразить их приложенными к точке на рисунке; 3. Освободить точку от связей, заменить связи их реакциями и также изобразить их на рисунке; 4. Добавить к полученной системе сил силу инерции; 5. Рассмотреть образовавшуюся уравновешенную систему сил и в зависимости от вида системы сил выбрать наиболее рациональный способ решения. Задача 1. По наклонной плоскости (рис. 10) АВ длиной 4 м с углом подъема α=150 равноускоренно поднимают груз весом G= 200 Н, постоянной силой P=65Н, направленной параллельно наклонной плоскости. Определить, сколько времени потребуется, чтобы переместить груз на расстояние АВ, если коэффициент трения при движении груза по наклонной плоскости ƒ=0,05 Решение. Изобразим тело на наклонной плоскости с приложенными к нему силами G и Р, а также силой трения Fтр и нормальной реакцией N наклонной плоскости. Находясь под действием этих сил, тело движется по наклонной плоскости с постоянным ускорением α. 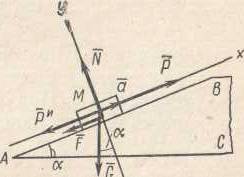 Рис. 10 Груз перемещается равноускоренно, без начальной скорости. Время движения можно определить из уравнения движения  , откуда  , но предварительно необходимо определить ускорение αТак как груз движется с ускорением, то силы G, P, N, F, приложенные к нему, не образуют уравновешенной системы. Приложим к грузу силу инерции Ри = mα =  , н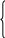аправив ее в сторону, противоположную ускорению α. Теперь система пяти сил G, P, N, Fтр, Ри является уравновешенной.4  . Выберем системы координат, спроектируем все силы на оси, получим два уравнения равновесия:ΣX=0; P-G sinα-Fтр-Pи=0 (1) ΣY =0; N-G cos α =0 (2) 5. Из уравнения (1) найдем Pи= P-G sinα-Fтр, где Fтр=ƒN Нормальное давление найдем из уравнения (2) N= G cos α Поэтому Pи= P-G sinα- ƒ G cos α=3,6 Н 6. Из выражения Ри = mα = найдем ускорение  = 0,18 м/с27. Подставив значение ускорения в выражение , найдем время перемещения груза по всей длине наклонной плоскости = =6,7 сПрименение принципа Даламбера при решении задач на криволинейное движение точки Как известно из кинематики, при движении материальной точки по криволинейной траектории ее ускорение α имеет два составляющих ускорения: α t - касательное (тангенциальное) и αn - нормальное (центростремительное). Из динамики уже известно, что ускорение α, приобретенное точкой, есть результат действия определенной системы сил. Равнодействующая Р этой системы и ускорение и находятся в зависимости, выражающей основной закон динамики точки: P=mα Если уравновесить силу Р приложением к точке силы инерции Ри, а затем разложить ее на две составляющие Риt Риn соответственно по нормали и по касательной, то эти составляющие будут находиться в зависимости от нормальных и касательных ускорений , определяемых такими векторными равенствами: Риt= - mαt и Риn= - mαn В задачах на криволинейное движение точки в основном рассматривается нормальная (центробежная) сила инерции Риn. Числовое значение нормальной (центробежной) силы инерции можно следующими формулами: Риn= - mαn. Заменим здесь  ;  Если материальная точка, рассматриваемая в задаче, связана с каким-либо вращающимся телом, то скорость точки удобнее выражать через угловую скорость тела v= ωr и тогда Риn=m ω 2 r Если в последней формуле выразить массу точки через ее вес  , а угловую скорость тела – в об/мин  то  ; если учесть, что π2= g (9,86≈9,81), поэтому  Эта формула дает приближенное значение центробежной силы ; но она очень удобна при решении многих задач. Последовательность решения задач на криволинейное движение при помощи метода кинетостатики та же. Методические указания к решению задач При решении задач с применением принципа Даламбера необходимо придерживаться следующего порядка: 1. Выбрать объект рассмотрения, принять его за материальную точку (систему материальных точек) и изобразить ее в текущий момент времени. Выбрать направление ускорения. 2. Приложить все активные (заданные) силы, действующие на точку. 3. Освободить точку от связей, заменив их действие реакциями. 4. Добавить силы инерции. 5. Составить уравнения кинетостатического равновесия. 6. Решить полученные уравнения, число которых должно быть равно числу неизвестных величин, входящих в уравнения. Задача 2. Шарик, масса которого m=0,5 кг, привязан к нити длиной 0,7 м (рис.11) Нить вместе с шариком вращается в вертикальной плоскости, затрачивая на один оборот 1 сек. Определить натяжение шнура в моменты высшего и низшего положения шарика, считая, что скорость остается постоянной при перемещении во всей длине окружности. 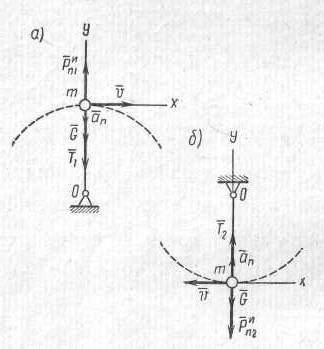 Рис. 11 Решение. 1. В соответствии с условием задачи считаем, что шарик движется равномерно по окружности, радиус которой равен длине (r = 0,7 м). Следовательно, его скорость  Оставаясь численно неизменной, скорость точки непрерывно изменяет направление, значит, точка имеет нормальное ускорение = =27,6 м/с22. Рассмотрим движущийся шарик в тот момент, когда он проходит через верхнюю точку траектории (Рис. 11, а). На шарик действуют две силы: его вес G и реакция нити Т1, равная ее натяжению. Заметим, что обе силы направлены в одну сторону - к точке О подвеса, так как вес всегда направлен вертикально вниз. Реакция гибкой связи всегда направлена вдоль нити от тела, которое удерживается нитью. Шарик, привязанный к нити и приведенный в движение, стремится согласно закону инерции двигаться равномерно и прямолинейно и поэтому он постоянно натягивает нить. 3. Добавим к силам G и Т силу инерции Риn, направив ее в сторону, противоположную ускорению αn. Образовав, таким образом, уравновешенную систему сил, получим уравнение равновесия ΣYi=0; Риn1- G - Т1=04. Из уравнения равновесия находим Т1, учитывая, что Риn1= mαn и G = mg: Т1= Риn1-G=m(αn-g), подставляя в это выражение числовые значения: Т1 = 0,5 (27 ,6- 9,81) = 0,5* 17,8 = 8,9 Н. Таким образом, находясь в верхнем положении, двигающийся шарик натягивает нить силой 8,9 Н. Отметим, что натяжение нити будет ослабевать при уменьшении скорости движения шарика. Следовательно, для того чтобы шарик при движении в вертикальной плоскости смог пройти верхнюю точку траектории с заданным радиусом кривизны р, он должен иметь в этой точке определенную скорость. 5. Рассмотрим теперь движущийся шарик в момент прохождения им нижней точки траектории (Рис.11, б) В этом положении на шарик действуют также две силы: вес G и реакция нити Т2, но в отличие от предыдущего случая эти силы, действуя вдоль одной прямой, направлены в противоположные стороны. 6. Добавим к силам G и Т2 силу инерции Ри и составим уравнение равновесия: ΣYi =0; Т2 - G - Риn2=0 7. Находим Т2: Т2 = G + Риn2= m (g+αn) = 0,5 (9,81 +27,6) = 18,7 Н.Как видно, при прохождении через нижнюю точку траектории шарик создает наибольшее натяжение. Пример 11 Тело под действием собственного веса (Рис.12 )скользит по негладкой наклонной плоскости, составляющей с горизонтом угол а = 45°. Определить ускорение движения, если коэффициент трения тела о плоскость f = 0,3 а) б) 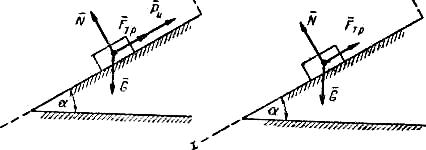 Рис. 12 Р ешение. Принимаем тело за материальную точку. Изобразим его на наклонной плоскости (Рис.12,а). Очевидно, что скорость v и ускорение α направлены вниз по наклонной плоскости. На материальную точку действует одна активная сила — вес G. Отбросим связь-плоскость и приложим нормальную реакцию N и силу трения FTP. Добавим силу инерции Fи; получим согласно принципу Даламбера уравновешенную систему сил. Направим оси координат х и у и составим уравнения кинетостатического равновесия:ΣХ =0 G sina —Fтр —Ри= 0; ΣY = 0, N — G cosa = 0. Из второго уравнения следует N = G cos a, тогда FTp = ƒN =ƒG cos a. Подставим в первое уравнение найденное значение Fтp и Ри= m a=G a /g: G sin a — ƒ G cosa — G α /g = 0. Решаем это уравнение относительно искомого ускорения: а = g (sin a — ƒcos a) = 9,81 (sin 45° — 0,3 cos 45°) = 4,84 м/сек2 Для сравнения решим эту же задачу при помощи уравнений движения (рис.12, б) Примем тело за материальную точку. Отбросим связь. На материальную точку действуют: G—сила веса; N— нормальная реакция; FTp —сила трения. Составим уравнения движения: m  ах = ΣX = G sin a — F тр,mаy = ΣY = N — G cos a. Согласно условию, αу =О, тогда из последнего уравнения находим N = Gcosa. Следовательно , Fтр = ƒ N = ƒG cosα. Подставим в первое уравнение значения F тр и m=G/g: G αх /g = G sin α— ƒG cos α. Искомое ускорение равно αx = α = g (sinα - f cos α) = 4,84 м/сек2 Тест №14 ДИНАМИКА Вариант 1
|
