Пояснительная записка Цель данного пособия помочь студентам глубже разобраться в разделах теоретической механики Кинематика

• Название: Пояснительная записка Цель данного пособия помочь студентам глубже разобраться в разделах теоретической механики Кинематика
• Дата: 23.12.2020
• Размер: 1.98 Mb.
• Имя файла: 00107dca-1ad52854.doc
• Тип: Методическое пособие; #163330
• страница: 8 из 15

Сложное движение точки.

В мире все находится в непрерывном движении, и неподвижная система координат в действительности не существует. Поэтому возникает необходимость рассматривать движение точек одновременно по отношению к двум системам отсчета, одна из которых считается неподвижной, а вторая определенным образом движется по отношению к первой. Движение точки в данном случае называется сложным.

Движение точки по отношению к неподвижной системе координат называется абсолютным. Движение точки по отношению к подвижной системе координат называется относительным. Движение подвижной системы координат по отношению к неподвижной называется переносным. Абсолютное движение является сложным и состоит из относительного и переносного движений.

В тех случаях, когда заданы движения двух или более тел (точек) относительно неподвижной системы координат и необходимо определить движение одного из этих тел относительно другого, удобно пользоваться расчленением абсолютного движения на переносное и относительное.

Тело, относительно которого требуется рассмотреть движение, мысленно остановим, а неподвижную систему координат заставим двигаться по его закону, но в обратном направлении. Тогда для второго тела это движение станет переносным, а движение второго тела - относительным. После этого просто понять, как будет двигаться второе тело по отношению к первому.

При изучении сложного движения точки будем рассматривать только перемещение и скорость.

Если переносное и относительное движения направлены вдоль одной прямой, то

1. 
   перемещение точки в абсолютном движении равно алгебраической сумме перемещений в переносном и относительном движениях.;
   
2. 
   скорость точки в абсолютном движении равна алгебраической сумме переносной и относительной скоростей.
   

Условимся направление переносного перемещения и соответственно направление переносной скорости считать положительными. Тогда относительное перемещение и соответственно относительная скорость будут также положительными, если они направлены в ту же сторону, что и переносное. Если же относительное перемещение имеют направление, противоположное переносному, то будем считать их отрицательными.

Таким образом, при совпадении направлений переносного и относительного движений

При противоположных друг другу направлениях переносного и относительного движений

Модуль абсолютной скорости находится по теореме косинусов:

, а направление по теореме синусов



Указания к решению задач:

1. 
   Выяснить, какое движение является абсолютным, какое относительным, какое переносным.
   
2. 
   Направить векторы абсолютной, относительной и переносной скоростей.
   
3. 
   Простроить параллелограмм или треугольник скоростей и из него найти неизвестные величины.
   

Пример 7.

Наклонная плоскость АВ (рис.6) с углом ВАС, равным 45⁰, движется прямолинейно с постоянной скоростью v=5 м/с. По плоскости скользит тело G со скоростью 2t . определить абсолютную скорость тела через 5 с после начала движения, считая, что в начальный момент относительная скорость тела G равнялась нулю.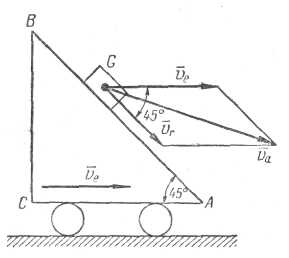



Рис.5

Решение.

Прямолинейное движение тела со скоростью 2t по движущейся плоскости – относительное V_отн.=2t. Прямолинейное движение наклонной плоскости с постоянной скоростью V_пер=5 м/с – переносное.

Таким образом, V_абс=V_пер+V_отн, угол между векторами V_пер и V_отн в параллелограмме скоростей = 45⁰, тогда

=

Определяем модуль абсолютной скорости в момент времени 5 секунд.

V_абс = √5²+ 45² + 10√2*5 =14 м/с

Пример 8.

Вниз по течению реки равномерно плывет лодка, приводимая в движение гребным винтом от мотора. Скорость течения реки 4 км/ч, скорость лодки, сообщаемая ей гребным винтом по отношению к воде, составляет 8 км/ч. Определить скорость лодки относительно берегов и расстояние, которое проходит лодка вдоль берегов за 20 мин.

Решение.

1. Лодку принимаем за материальную точку, а водную массу реки – за материальную среду.

Движение лодки относительно берегов или, иначе говоря, движение лодки, наблюдаемое с берега, - это абсолютное движение.

Переносное движение лодки – ее перемещение вместе с рекой; скорость – 4 км/ч, которую сообщает лодке река, - ее переносная скорость.

Относительное движение – перемещение лодки по поверхности воды, создаваемое гребным винтом, скорость относительного движения – 8 км/ч.

2. Так как в данном случае переносное и относительное движения направлены в одну и ту же сторону, то скорость лодки относительно берегов (абсолютная скорость)

V_абс =V_реки+ V_лодки= 4+8 = 12 км/ч

3. За время t = 20 мин = часа лодка вдоль берегов проходит расстояние S_абс= V_абс t = 12 * = 4 км.

Для самостоятельного решения.

Задача

С какой скоростью относительно берегов будет перемещаться лодка и какое расстояние она проплывет за 30 мин, если будет двигаться против течения?

Ответ: V_абс= 4 км/ч S_абс=2 км

Сложное движение твердого тела

Плоскопараллельным движением твердого тела называют такое движение, при котором все точки движутся в плоскостях, параллельных некоторой неподвижной плоскости.

Плоскопараллельное движение является сложным, состоящим из переносного поступательного вместе с выбранным полюсом и относительного вращательного движений вокруг полюса. Отметим, что скорость поступательного движения зависит от выбора полюса, а угловая скорость вращательного движения не зависит от выбора полюса.

Применяют три способа определения скоростей точек плоской фигуры:

1 способ. (рис.6, а)

Скорость любой точки плоской фигуры равна геометрической сумме скорости полюса V_А и скорости той же точки во вращательном движении данной фигуры относительно полюса V_ВА: V_В = V_А +V _ВА.

При этом скорость полюса V_А по существу является переносной скоростью точки В, а скорость во вращательном движении вокруг полюса V _ВА – относительной скоростью точки В. Модуль относительной скорости V _ВА=ω АВ, где ω – угловая скорость плоской фигуры.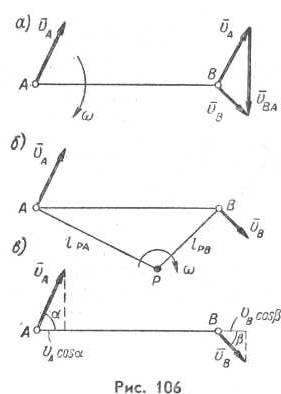




Рис.6

2 способ. (рис.6, б) В любой момент времени в плоскости фигуры можно найти такую точку Р, абсолютная скорость которой равна нулю V_P =0. Точку Р называют мгновенным центром скоростей плоской фигуры. Скорость любой другой точки А этой плоской фигуры равна вращательной скорости той же точки вокруг мгновенного центра скоростей.

V_А=АР ω.

3 способ. (рис.6, в) Если при плоскопараллельном движении фигуры известны модуль и направление одной точки А и направление другой точки В, то неизвестный модуль точки В можно определить по следующей теореме: проекции скоростей концов неизменяемого отрезка на направление этого отрезка равны между собой, т.е. ПР_АВ V_A= ПР_АВ V_B.

Пусть на отрезке АВ известны V_A, α, β и направление V_В. Требуется определить модуль V_В. Тогда ПР_АВ V_A= V_A cos α, ПР_АВ V_В= V_В cos β,

Подставляя проекции скоростей в ПР_АВ V_A= ПР_АВ V_B, находим V_В= V_A cos α/ cos β.

Определение мгновенного центра скоростей.

При решении задач возможны следующие случаи:

1.Известны вектор скорости одной точки V_A и угловая скорость вращения плоской фигуры ω (рис.7, а). Мгновенный центр скоростей находится на перпендикуляре, восстановленном из точки А к направлению вектора скорости, на расстоянии АР = V_A/ ω.

Если мгновенный центр скоростей при движении тела остается неподвижным, то плоское движение превращается во вращательное.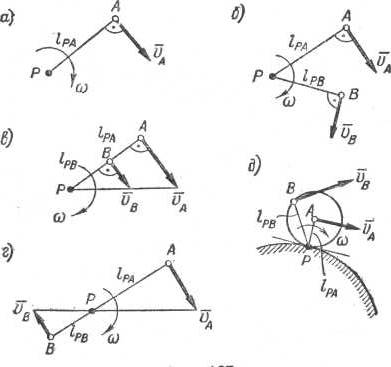


Рис. 7

2. Известны только направления скоростей двух точек А и В, причем линии действия векторов скоростей пересекаются (рис.7, б). Мгновенный центр скоростей находится в точке пересечения перпендикуляров, восстановленных в этих точках, к направлению их скоростей.

Так как V_A= АР ω и V_В= ВР ω, то V_A/ V_В=АР/ВР. Если скорости двух точек параллельны и направлены в одну сторону, а прямая, соединяющая эти точки, не перпендикулярна направлению скоростей, то тело движется поступательно

3. Известны векторы двух точек V_A и V_В, причем V_A и V_В параллельны и направлены в одну сторону (рис.7, в). Прямая, соединяющая эти точки, перпендикулярна направлению скоростей. Мгновенный центр скоростей находится на пересечении прямой, проведенной через концы векторов V_A и V_В , и продолжении прямой АВ , со стороны точки, имеющей меньшую скорость. Расстояния от мгновенного центра скоростей до точек А и В пропорциональны модулям скоростей.

V_A/АР= V_В/ВР.

Если V_A = V_В, то в данный момент тело движется поступательно. В этом случае мгновенный центр скоростей находится в бесконечности. Скорости всех точек плоской фигуры геометрически равны, а скорость вращения вокруг любого полюса равна ω=0

4. Векторы V_A и V_В параллельны, но направлены в разные стороны (рис.7, г). Мгновенный центр лежит на отрезке АВ и делит его на части, пропорциональные величинам скоростей.

V_A/АР= V_В/ВР

5. 
   Плоская фигура катится без скольжения по неподвижной кривой
   

(рис.7, г). Мгновенный центр скоростей Р находится в точке касания фигуры с кривой.

Пример 9 Стержень АВ двигается в плоскости чертежа. В момент, когда стержень занимает горизонтальное положение(рис.8, а), скорость его точки А равна 2 м/с и направлена под углом 60⁰ к прямой АВ. Определить скорость точки В, если известно, что она направлена вдоль АВ.

Решение 1. Сложение переносной и относительной скоростей (рис.8, б)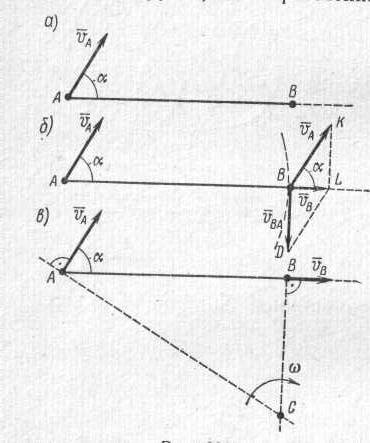



Рис. 8

1. 
   Примем за полюс точку А. Вместе с полюсом стержень АВ движется поступательно, поэтому точка В как слагаемая скорость имеет скорость полюса, т.е. V_A, которую изобразим у точки В вектором ВК.
   
2. 
   Вследствие вращения стержня вокруг полюса точка В имеет вторую слагаемую скорость V_ВA – относительную скорость, направленную перпендикулярно к стержню.
   
3. 
   Построим параллелограмм скоростей. В параллелограмме известно направление диагонали, которая изобразит искомую скорость V_В; поэтому из точки К проведем до пересечения с продолжением АВ отрезок KL, параллельный направлению относительной скорости V _ВA. Затем из точки L проведем прямую LD, параллельную КВ ( или вектору V_A), до пересечения в точке D с линией, характеризующей направление V _ВA. Получается параллелограмм BKLD, в котором диагональ BL изображает V _В - скорость точки В.
   
4. 
   Находим числовое значение V _В: Треугольник BLK – прямоугольный, поэтому V _В= V _A cos α= 2 cos 60⁰ = 1 м/c.
   

Решение 2. При помощи мгновенного центра скоростей (рис.8, в).

1. 
   Из точек А и В проведем две прямые, перпендикулярные к направлениям скоростей V _В и V _A. Точка С пересечения этих прямых и определит положение МЦС.
   
2. 
   Вращение стержня АВ вокруг МЦС С в данный момент характеризуется угловой скоростью ω. Поэтому V _В/ ВG= V _A/ AC = ω.
   

Отсюда V _В = V _A ВС/АС, но т.к. угол ВСА =α, то ВС/АС = cos α, следовательно

V _В = V _A cos α= 2 cos 60⁰ = 1 м/c.

Решение 3. С применением теоремы о проекциях скоростей двух точек плоского сечения.

1. В рассматриваемом случае искомая скорость V _В направлена вдоль прямой, соединяющей точки А и В, при этом известен угол между данной скоростью V _А и той же прямой АВ. Поэтому удобно применить теорему: проекции скоростей концов неизменяемого отрезка на направление этого отрезка равны между собой.

2. Спроектировав данную скорость V _А и искомую скорость V _В на прямую АВ (рис.4,в) и приравняв эти проекции, получим

V _В = V _A cos α, откуда V _В = V _A cos α= 2 cos 60⁰ = 1м/c.

Основные понятия динамики

Предмет динамики.

В динамике изучают движение механи­ческой системы материальных точек, в связи с действующими на нее силами.

Аксиомы (законы) динамики.

В основе динамики лежат четыре аксиомы (закона), сформулированные Исааком Ньютоном.

Первая аксиома (Закон инерции). Всякая материальная точка сохраняет состояние покоя или равномерного прямоли­нейного движения до тех пор, пока внешние силы не выведут её из этого состояния.

Если тело движется прямолинейно, то на него или совсем не действуют никакие силы (идеальный случай) или действует уравновешенная система сил (реальный случай).

Всякая материальная точка обладает инертностью, т. е. она стремится сохранять состояние покоя или равномерного прямо­линейного движения. Другими словами, инертность — свойство сохранять скорость (по модулю и по направлению).

Сама материальная точка, без участия внешних сил, не может изменить свою скорость.

Вторая аксиома (Основное уравнение динамики точки). Сила равна массе, умноженной на ускорение Р = mа.

Так как масса — величина скалярная, то вектор силы направ­лен в ту же сторону, что и вектор ускорения.

Чем больше масса, тем большую силу необходимо приложить к точке, чтобы изменить ее скорость. Следовательно, масса является мерой инертности.

Всякая материальная точка притягивается к Земле с силой, кото­рую называют весом. Чем больше масса материальной точки, тем больше ее вес. Следовательно, масса является и мерой тяжести.

В применении к свободному падению (притяжению к Земле) второй закон Ньютона имеет вид mg=G, где g – ускорение свободного падения, зависящее от географической широты местности; G – сила веса тела.

Третья аксиома (Закон независимости действия сил).

Если на материальную точку действуют несколько сил одновременно, то точка имеет такое же ускорение, какое она получит от равнодействующей этой системы сил.

Это означает, что вместо того, чтобы находить ускорение материальной точки как сумму α = α₁ + α₂ +….+ α_n =P₁/m + P₂/m + …+P_n/m, достаточно определить равнодействующую и ускорение найдется как отношение α =P/m

Действие силы на точку не зависит от того, действует ли сила одна или совместно с другими силами, а также и от того, находится ли точка в покое или в движении.

Четвертая аксиома (Закон равенства действия и противодействия). Действия двух тел друг на друга всегда равны и направлены в противоположные стороны.

Если тело А действует на тело В с силой Р₁; то и тело В действует на тело А с силой Р₂ = — Р₁

Идеальные и реальные связи. Связи, в которых отсутствует трение, называют идеальными. Реакции таких связей всегда перпендикулярны опорной поверхности. В природе существуют только связи с трением, их называют реальными. Полная реак­ция такой связи всегда отклонена от нормали

При решении задач реакцию опорной поверхности обычно представляют двумя составляющими: нормальной реакцией N и силой трения F_TP.

При движении величина силы трения связана с нормальной реакцией законом Кулона F_TP= ƒ N,

где ƒ — коэффициент трения движения (в отличие от коэффи­циента трения покоя), зависящий от материалов и обработки трущихся поверхностей и скорости их взаимного перемещения. Обычно изменением f с увеличением или умень­шением скорости пренебрегают и считают его постоянным.