Пояснительная записка Цель данного пособия помочь студентам глубже разобраться в разделах теоретической механики Кинематика

• Название: Пояснительная записка Цель данного пособия помочь студентам глубже разобраться в разделах теоретической механики Кинематика
• Дата: 23.12.2020
• Размер: 1.98 Mb.
• Имя файла: 00107dca-1ad52854.doc
• Тип: Методическое пособие; #163330
• страница: 9 из 15

Тест №13

Законы Ньютона. Сила. Единицы силы

Для каждого вопроса группы А указать правильный ответ из группы А, для каждого вопроса группы В указать правильный ответ из группы В

Вопросы группы А

1. 
   Что называется инерцией тела?
   
2. 
   В чем состоит первый закон Ньютона?
   
3. 
   Как будет двигаться тело без воздействия на него других тел?
   
4. 
   Что называется силой?
   
5. 
   Чем характеризуется сила как вектор?
   
6. 
   В чем состоит второй закон Ньютона?
   
7. 
   Что называется массой тела?
   
8. 
   Что такое вес тела?
   
9. 
   В чем состоит третий закон Ньютона?
   

Вопросы группы В

1. 
   Как математически записывается второй закон Ньютона?
   
2. 
   Как математически записывается третий закон Ньютона?
   
3. 
   Укажите формулу веса тела
   
4. 
   Что принимается за единицу силы в СИ?
   
5. 
   Как называется единица веса в СИ?
   
6. 
   Что принимается за единицу силы в системе МКГСС?
   
7. 
   Как называется единица веса в СИ?
   
8. 
   Как движется тело под действием постоянной силы?
   
9. 
   Какое соотношение между 1 килограмм-силой и 1 Н?
   

№ вопр.	Ответы гр.А	№ вопр.	Ответы гр.В
	…всякое воздействие на данное тело, сообщающее ускорение или вызывающее его деформацию		a1 m1= - a2 m2
	…скалярная величина, являющаяся мерой инертности тела		…сила вызывает равномерное прямолинейное движение
	…величина, измеряемая силой, с которой тело притягивается к Земле		…Ньютон
	…свойство тел сохранять свое состояние покоя или прямолинейного равномерного движения		…сила вызывает равноускоренное прямолинейное движение
	Всякому воздействию соответствует равное, но противоположно направленное противодействие		P=mg
	Ускорение тела прямопропорционально действующей силе, обратнопропорционально массе и совпадает по направлению с силой		…сила, с которой притягивается к земле тело массой в 1 кг на уровне моря и на широте 450
	…величиной, направлением и точкой приложения		1кГ=9,8Н
	Всякое тело сохраняет состояние относительного покоя или равномерного прямолинейного движения до тех пор, пока другие тела не выведут его из этого состояния		…такая сила, которая телу массой 1 кг сообщает ускорение в 1 м/с2
	Сила, действующая на тело, прямопорциональна массе тела и обратнопропорциональна его ускорению		a= F/m
	…равномерно и прямолинейно		1Н=9,8 кГ

Две задачи динамики материальной точки

Уравнения движения материальной точки

Свободная и несвободная материальная точка. Материальную точку, на которую не наложены никакие связи, называют сво­бодной, а ее движение — свободным. Такая материальная точка может занимать любое положение в пространстве, и ее движение зависит только от начальных условий и действующих на нее активных (заданных) сил.

Материальную точку, на движение которой наложены какие-либо связи, называют несвободной, а ее движение несвободным.

Такая точка под действием активных сил не может, благо­даря наложенным на нее связям, занимать произвольное поло­жение или иметь произвольную скорость.

На основании второй и третьей аксиом динамики имеем

mα = P = ΣP_i,

где m — масса материальной точки; α— ее ускорение; Р — равнодействующая всех сил, приложенных к этой точке.

При свободном движении в ΣP_i войдут только активные силы. Если же движение несвободное, то сначала отбрасывают связи и заменяют их действие силами реакций связей (т. е. при­меняют принцип освобождаемости от связей). Затем несвобод­ную материальную точку рассматривают как свободную, тогда в число ΣP_i; войдут и активные силы и реакции связей.

Обычно массу материальной точки находят как отношение ее веса G, выраженного в Н (СИ), к уско­рению силы тяжести g, в м/сек², т. е.

m=G/g

У 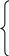равнения движения материальной точки в декартовой системе координат. Проектируя векторное равенство mα = P = ΣP_i на оси декар­товой системы координат, получаем уравнения движения мате­риальной точки в этой системе:

mα_x=ΣX_i=X

mα_y=ΣY_i=Y

mα_z=ΣZ_i=Z

где α_х, α_y, α_z — проекции ускорения;

X, Y, Z— проекции равнодействующей силы на соответст­вующие оси.

Так как проекция ускорения на какую-либо ось — есть первая производная от соответствующей проекции скорости или вторая производная от координаты, то эти уравнения можно записать иначе:


m dx/dt= ΣX_i

m 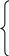dy/dt= ΣY_i

m dz/dt= ΣZ_i

или

m 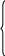d ²x/dt ²= ΣX_i

m d ²y/dt ²= ΣY_i

m d ²z/dt ²= ΣZ_i

Уравнения движения, записанные в такой форме, называют дифференциальными уравнениями движения материаль­ной точки.

Если точка движется прямолинейно, то, принимая траекто­рию точки за ось x, получаем ma = ΣX_i

Уравнения движения в естественных осях. Проектируя век­торное равенство mα = P = ΣP_i на естественные оси, получаем уравне­ния движения в естественных осях:

ma_t =P_t

ma_n = P_n

где a_t и a_n -тангенциальное и нормальное ускорения точки;

P_t и P_n —проекции действующей силы (равнодействующей) соответственно на касательную и нормаль.

Эти же уравнения можно записать в дифференциальной форме:

m dv/dt= P_t

m v²/ρ= P_n,

где v — скорость точки;

ρ — радиус кривизны траектории..

Пользуясь данными уравнениями , можно решать две основные задачи динамики точки.

Первая основная задача динамики материальной точки

По заданному закону движения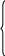


x = f₁(t),

y = f₂(t),

z= f₃(t)
и массе m материальной точки найти силу Р, действующую на эту точку.

Эта задача сводится к нахождению ускорения. Методы опре­деления ускорения зависят от способа задания движения.

Определенные проекции ускорения на декартовы (или естественные) оси координат следует подставить в уравнения движения и найти проекции действующей (равнодействующей) силы на соответствующие оси:

Х = mа_х; Y = ma_y Z = ma_z.

Модуль и направление силы, действующей на точку, нахо­дят по формулам:



cos (Р, х) = ; cos (Р, у) = ; cos (Р, z) =

Аналогично решаем задачу в естественных осях:

P_t = ma_t; P_n = ma_n

Откуда cos(P, t)= ; cos(P, n) =

Методические указания к решению задач

При решении первой основной задачи динамики точки реко­мендуется придерживаться следующего порядка:

1. Выбрать объект рассмотрения, приняв его за материаль­ную точку. Изобразить её в текущий момент времени.

2. Приложить активные (заданные) силы, действующие на точку.

3. Освободить точку от связей в (случае несвободной точки), заменив действие отброшенных связей реакциями.

4. Выбрать систему координат.

5. Составить уравнения движения точки (в тех случаях, когда траектория точки — окружность, удобнее составлять урав­нения движения в естественной форме).

6. Определить проекции ускорения на выбранные оси коор­динат по заданному закону движения и подставить в уравнения движения.

7. Найти проекции действующей (равнодействующей) силы на оси координат.

8. При необходимости по формулам



cos (Р, х) = ; cos (Р, у) = ; cos (Р, z) =

P_t = ma_t; P_n = ma_n

cos(P, t)= P_t/P; cos(P, n) = P_n/P определить модуль и направление искомой силы.

Пример 10 Каково натяжение троса, на котором подни­мается лифт весом G=10000 H с грузом Q = 25000 н, если за t = 2 сек скорость подъема возросла с V₀=1 м/сек до V_k = 2,5 м/сек, движение считать равноускоренным (рис.9)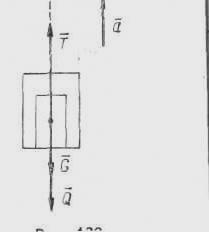



Рис. 9

Решение. Принимаем лифт с грузом за материальную точку. К материальной точке приложены активные силы: G — вес лифта; Q — вес груза. Отбрасываем связь: разрезаем трос и заме­няем его действие натяжением Т. Направляем ось х. В данной задаче все силы направлены вдоль оси х, поэтому достаточно составить одно уравнение дви­жения:

mа_х=ΣX= T-G-Q

Согласно условию, лифт движется с постоянным ускорением ;

масса материальной точки ;

Подставляем m и а_х в уравнения движения

* = T-G-Q

Полученное уравнение содержит одно неизвестное искомое натяжение

T=(G+Q) (1+(V_к- V₀)/ g t=( 10000+25000) (1+(2,5-1,0)/(9,8 -2)=37700 Н
Вторая основная задача динамики материальной точки

По заданным силам P(ΣPj), действующим на материальную точку, и её массе m найти закон движения:

x = ƒ₁ (t)

y = ƒ₂ (t)

z = ƒ₃ (t)

Зная силы, из уравнений движения можно определить уско­рение. Но одного ускорения недостаточно для определения закона движения. Необходимо знать скорость и положение точки в начальный момент времени, т. е. начальные условия.

Рассмотрим простейший случай — все силы, действующие на точку, постоянны (тогда и ускорение, получаемое точкой, тоже постоянно), т. е. точка должна двигаться равноускоренно или равнозамедленно.

При решении второй задачи динамики точки необходимо придерживаться следующего порядка:

1. Принять рассматриваемый объект за материальную точку и изобразить ее в текущий момент времени.

2. Приложить активные (заданные) силы, действующие на материальную точку.

3. Освободить точку от связей (в случае несвободной точки), заменив действие связей реакциями.

4. Выбрать систему координат (если точка движется по окруж­ности, то следует выбрать систему естественных осей).

5. Составить уравнения движения точки в выбранной системе координат.

6. Выразить проекции ускорения через искомые кинематиче­ские элементы (проекций скоростей, координаты, время) и подставить в уравнения движения.

7. Решить уравнения относительно искомых величин.
Кинетостатика материальной точки

Силы инерции

Всякое ускорение — следствие действия силы, а сила - мера механического взаимодействия двух материальных точек. Силой инерции Р_и материальной точки М называют произведение массы этой точки на ее ускорение, взятое с обратным знаком: Р_и= – mα

Сила инерции Р_и материальной точки M, движущейся под действием активной силы Р и силы реакции связи N, реально существует, но она приложена не к точке М, а к телам, меха­нически взаимодействующим с точкой М и к связям, наложен­ным на эту точку.

При прямолинейном движении направление ускорения совпа­дает с траекторией. Если движение ускоренное, то сила инерции направлена в сторону, противоположную скорости, если замед­ленное, то сила инерции совпадает по направлению со скоростью.

При криволинейном движении полную силу инерции Р_и целе­сообразно разложить на две составляющие: нормальную (центробежную) силу инерции

Р_иn- mα_n и тангенциальную (касательную) силу инерции P_иt= - mα_t.

Тогда P_и= Р_иn+ P_иt

Модуль полной силы инерции определяют по формуле



При решении задач обычно ограничиваются определением составляющих Р_иn и P_иt

Частные случаи:

а) движение равномерное и прямолинейное. Тогда

dv/dt=α_t=0; ρ=∞ и P_и= m √(dv/dt)² + (v²/ρ)²= m √0+(v²/∞)² =0

б) движение прямолинейное с постоянным ускорением α.

Тогда dv/dt= α_t= α; ρ=∞ и P_и= m √α² + (v²/∞)²= m α

в) равномерное движение по окружности радиусом г с угловой скоростью ω. Тогда dv/dt= 0; ρ=r; v=ω r; P_и= m√(0)² + (ω² r²/ r)² =m ω²r

г) равноускоренное движение по окружности радиусом r с угло­вым ускорением ε. При этом dv/dt=α_t= ε r; ρ=r; v=ω r и

P_и=m √ (ε r)² + (ω² r²/ r )²= m r √ ε² + ω⁴

Полную силу инерции лучше представить двумя составляю­щими тангенциальной Р_иt = m ε r и нормальной Р_иn = m ω²r

Принцип Даламбера (кинетостатики)

Принцип Даламбера для материальной точки формулируется следующим образом: в каждый момент времени все силы, дейст­вующие на точку, уравновешиваются силой инерции, т. е.

ΣР + Р_И = 0.

П роектируя векторное равенство на оси декартовой системы координат, получаем три скалярных равенства:

ΣX+ Р_Иx=0

ΣY+ Р_Иy=0

ΣZ+ Р_Иz=0,

где Р_Иx, Р_Иy, Р_Иz —проекции силы инерции на соответствующие оси. Проектируя на естественные оси, получаем:

ΣP_t +P_иt =0

ΣP_n +P_иn =0

При этом в число действующих сил ΣP входят активные силы и реакции связей.

Принцип Даламбера позволяет задачи динамики решать как статические. Добавив силы инерции, можно применять все тео­ремы, законы и правила, доказанные и принятые в статике. Раздел, связанный с принципом Даламбера, получил название «кинетостатика» (что означает статика в движении).

В механической системе материальных точек, некоторым образом связанных между собой, можно рассматривать кинетостатическое равновесие не только каждой точки, но и всей системы в целом и любой ее части. При этом необходимо при­кладывать силы инерции к каждой материальной точке.

Всякое твердое тело можно представить как систему мате­риальных точек. Приложив к каждой точке силу инерции и сло­жив их, определяем силу инерции твердого тела. Она приложена в центре его тяжести С и равна

Р_И= - mα_t, где m — масса тела, а α_t — ускорение центра тяжести. Принцип Даламбера для движущегося тела имеет такое же выражение, как и для материальной точки:

ΣP_i+P_и=0, где ΣP_i — сумма всех сил, действующих на тело (активных сил и реакций связей).

Для направления вектора силы инерции необходимо знать направление ускорения. Выберем любое направление и решим задачу. Если в результате решения ускорение получается со знаком «плюс», то направление выбрано верно, если со знаком «минус», значит, надо изменить его на противоположное.

Необходимо учитывать, что только при решении задач мето­дом кинетостатики необходимо добавлять силы инерции.