ПРОЕКТ УКЛАДКИ БЕССТЫКОВОГО ПУТИ. Пояснительная записка к дипломному проекту д 230506 456 пз разработал студент (подпись)
 Скачать 6.45 Mb. Скачать 6.45 Mb.
|
1.2 Расчеты пути на прочность1.2.1 Общие сведенияПри воздействии подвижного состава в элементах верхнего строения пути возникают напряжения и деформации. Зависимость их от сил, действующих на путь, сложна и пока не поддается точному определению. Поэтому в Правилах расчета железнодорожного пути на прочность [9] приняты следующие правила и предпосылки. Рельс считается балкой бесконечно большой длины неизменяемого сечения, лежащей на сплошном равноупругом основании. Путь и подвижной состав находятся в исправном состоянии, отвечающем требованиям ПТЭ. Колеса подвижного состава при движении не отрываются от поверхности катания рельсов (рассматривается безударное движение). Расчет ведется на вертикальные силы, приложенные по оси симметрии рельса. Из продольных горизонтальных сил учитываются только температурные силы, появляющиеся в рельсах. Упругая реакция основания считается линейно зависящей от осадки. Характеристики пути считаются постоянными величинами. Влияние климатических факторов учитывается лишь при температурных воздействиях на рельсы и изменениях жесткости пути при промерзании шпал, балласта и земляного полотна. Ввиду относительно небольшого влияния соседних колес принимается допущение, что давления от них имеют средние значения. Собственные напряжения и неупругие сопротивления не учитываются. Колебания массы колеса и пути в расчетах учитываются коэффициентом α0 (α0=0,401, αп=1,48 для пути с железобетонными шпалами). За расчетное сечение пути принимаем сечение в зоне влияния изолированной неровности пути, которое экипаж проходит со сжатыми рессорами. Дисбаланс колес не учитывается. Рельс рассчитывается только на нормальное напряжение изгиба. Расчет ведется по одному рельсу. Несмотря на большое количество допущений, и предпосылок, расчет дает достаточно удовлетворительные результаты, совпадающие с экспериментальными данными. Влияние допущений и неучтенных факторов компенсируется в расчетах введением коэффициента запаса Кн=1,3. Допускаемое расчетное напряжение от поездной нагрузки определяется из выражения 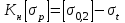 , (1.1) , (1.1)где 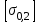 - допускаемое напряжение рельсовой стали; - допускаемое напряжение рельсовой стали;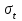 - температурные напряжения, действующие в рельсе. - температурные напряжения, действующие в рельсе.За допускаемое напряжение 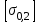 принимается гарантированный предел текучести рельсовой стали. принимается гарантированный предел текучести рельсовой стали.Допускаемое расчетное напряжение в рельсах бесстыкового пути, МПа, (с термоупрочненными рельсами) определяется как 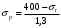 , МПа. (1.2) , МПа. (1.2)1.2.2 Расчет верхнего строения пути на прочность Вертикальная динамическая максимальная нагрузка 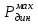 , кг, колеса на рельс [9] определяется по формуле , кг, колеса на рельс [9] определяется по формуле 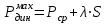 , (1.3) , (1.3)где Рср – среднее значение вертикальной нагрузки колеса на рельс, кг; λ – нормирующий множитель, определяющий вероятность появления 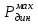 , для расчетов принимаем λ = 2,5; , для расчетов принимаем λ = 2,5; S – среднее квадратическое отклонение динамической вертикальной нагрузки колеса на рельс, кг. Среднее значение вертикальной нагрузки Рср, кг, колеса на рельс определяется по формуле 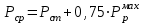 , (1.4) , (1.4)где Рст – статическая нагрузка колеса на рельс, кг (см. табл. 1.2); 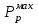 - динамическая максимальная нагрузка колеса на рельс, возникающая за счет колебания кузова на рессорах, кг. - динамическая максимальная нагрузка колеса на рельс, возникающая за счет колебания кузова на рессорах, кг.Динамическая максимальная нагрузка колеса на рельс 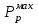 , кг, возникающая за счет колебания кузова на рессорах определяется по формуле , кг, возникающая за счет колебания кузова на рессорах определяется по формуле 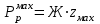 , (1.5) , (1.5)где Ж – жесткость рессорного подвешивания, приведенная к колесу, кг/мм (см. табл. 1.2); zмах – динамический прогиб рессорного подвешивания для 4-осного вагона определяется по формуле 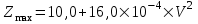 (1.6) (1.6)Среднее квадратическое отклонение динамической вертикальной нагрузки колеса на рельс от вертикальных колебаний S, кг, определяется по формуле 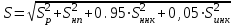 , (1.7) , (1.7)где Sp – среднее квадратическое отклонение динамической нагрузки колеса на рельс от вертикальных колебаний надрессорного строения, кг; Sнп- среднее квадратическое отклонение динамической нагрузки колеса на рельс от сил инерции необрессоренных масс при прохождении колесом изолированной неровности пути, кг; Sннк - среднее квадратическое отклонение динамической нагрузки колеса на рельс от сил инерции необрессоренных масс, возникающих из-за, кг; Sинк - среднее квадратическое отклонение динамической нагрузки колеса на рельс от сил инерции необрессоренных масс, возникающих из-за наличия на поверхности катания колес плавных изолированных неровностей, кг. Среднее квадратическое отклонение динамической нагрузки колеса на рельс от вертикальных колебаний надрессорного строения 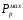 , кг, определяется по формуле , кг, определяется по формуле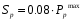 . (1.8) . (1.8)Среднее квадратическое отклонение динамической нагрузки колеса на рельс от сил инерции необрессоренных масс 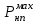 , кг, при прохождении колесом изолированной неровности пути определяется по формуле , кг, при прохождении колесом изолированной неровности пути определяется по формуле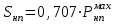 , (1.9) , (1.9)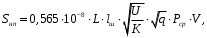 (1.10) (1.10)где L - коэффициент, учитывающий влияние на образование динамической неровности пути, типа шпал, типа рельсов, род балласта, материала шпал (см. табл. 1.3); lш – расстояние между осями шпал: при эпюре шпал 1840 шт./кмlш =55см; при 2000 шт./км - lш =51 см; U - модуль упругости рельсового основания, (см. табл. 1.3); К – коэффициент относительной жесткости рельсового основания и рельса, см-1; 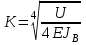 , (1.11) , (1.11)где E – модуль упругости рельсовой стали, E=2,1∙106 кг/см2; Jв – момент инерции поперечного сечения рельса относительно его центральной горизонтальной оси, проходящей через его центр тяжести, см4 (см. табл. 1.3) q - веснеобрессоренных частей экипажа, отнесенный к одному колесу, кг (см. табл. 1.2); Рср – среднее значение вертикальной нагрузки колеса на рельс, кг; V – скорость движения экипажа, км/ч. Среднее квадратическое отклонение Sннк, кг, динамической нагрузки колеса на рельс от сил инерции необрессоренных масс 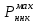 , кг, при движении колеса с плавной непрерывной неровностью поверхности катания определяется по формуле , кг, при движении колеса с плавной непрерывной неровностью поверхности катания определяется по формуле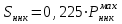 , (1.12) , (1.12)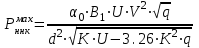 , (1.13) , (1.13)где α0 – коэффициент, характеризующий отношение необрессоренной массы колеса к участвующей во взаимодействии массе пути (см. табл. 1.3); β1 - коэффициент, характеризующий степень неравномерности образования проката поверхности катания, β1 = 0,23; U - модуль упругости рельсового основания, кг/см2, d – диаметр колеса, см (см.табл.1.2). Расчетная формула после подстановки известных численных значений приобретет вид 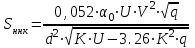 . (1.14) . (1.14)Среднее квадратическое отклонение Sинк, кг, динамической нагрузки колеса на рельс от сил инерции необрессоренных масс 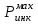 , кг, при движении колеса с плавной изолированной неровностью на поверхности катания определяется по формуле , кг, при движении колеса с плавной изолированной неровностью на поверхности катания определяется по формуле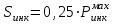 , (1.15) , (1.15)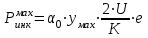 , (1.16) , (1.16)где е – расчетная глубина плавной изолированной неровности на поверхности катания колеса, принимается равной 2/3 от предельной допускаемой глубины неровности, е=0,067 см; умах – максимальный дополнительный прогиб рельса при прохождении колесом конусоидальной неровности, отнесенной к единице глубины неровности, умах = 1,47, см. Максимальная эквивалентная нагрузка 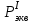 , кг, для расчетов напряжений в рельсах от изгиба и кручения определяется по формуле , кг, для расчетов напряжений в рельсах от изгиба и кручения определяется по формуле 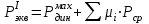 , (1.17) , (1.17)где 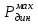 - динамическая максимальная нагрузка от колес на рельс, кг; - динамическая максимальная нагрузка от колес на рельс, кг;μi – ординаты линии влияния изгибающих моментов рельса в сечениях пути, расположенных под колесными нагрузками от осей экипажа, смежных с расчетной осью (см. табл. 1.4); Рср – среднее значение вертикальной нагрузки колеса на рельс, кг. Максимальная эквивалентная нагрузка 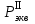 , кг, для расчетов напряжений и сил в элементах подрельсового основания определяется по формуле , кг, для расчетов напряжений и сил в элементах подрельсового основания определяется по формуле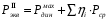 , (1.18) , (1.18)где 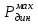 - динамическая максимальная нагрузка от колес на рельс, кг; - динамическая максимальная нагрузка от колес на рельс, кг;ηi – ординаты линии влияния прогибов рельса в сечениях пути, расположенных под колесными нагрузками от осей экипажа, смежных с расчетной осью (см. табл. 1.4); Рср – среднее значение вертикальной нагрузки колеса на рельс, кг. Определение расчетной оси Для получения наибольших напряжений в рельсах необходимо иметь от системы заданных сил максимальное значение изгибающего момента 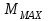 , а для напряжений на шпале, в балласте и на основной площадке земляного полотна – максимальное значение нагрузки на шпалу , а для напряжений на шпале, в балласте и на основной площадке земляного полотна – максимальное значение нагрузки на шпалу 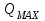 . Они возникают под одним из колес расчетной оси. . Они возникают под одним из колес расчетной оси.При определении наибольших напряжений от изгиба и кручения в рельсах от воздействия эквивалентной нагрузки 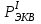 за расчетную ось принимается первая ось (рис. 1.1). Аналогично принимается при расчетах наибольших напряжений и сил в элементах подрельсового основания от воздействия эквивалентной нагрузки за расчетную ось принимается первая ось (рис. 1.1). Аналогично принимается при расчетах наибольших напряжений и сил в элементах подрельсового основания от воздействия эквивалентной нагрузки 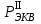 . .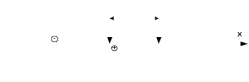 Рисунок 1.1 - Схема для определения наименее выгодного положения нагрузки (выбора расчетной оси). Максимальные напряжения изгиба и кручения в рельсах при воздействии вертикальных внецентренно приложенных и горизонтальных поперечных сил от колес подвижного состава определяются по формулам 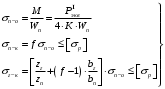 , (1.19) , (1.19)где σ п-о – осевое напряжение в подошве рельса, кг/см2; σ п-к – напряжение в кромке подошвы рельса, кг/см2; σ г-к – напряжение в кромке головки рельса, кг/см2; Wn – момент сопротивления рельса относительно наиболее удаленного волокна на подошве, см3 (см. табл. 1.3); К – коэффициент относительной жесткости рельсового основания и рельса, см -1; 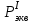 - максимальная эквивалентная нагрузка для расчетов напряжений в рельсах от изгиба и кручения, кг; - максимальная эквивалентная нагрузка для расчетов напряжений в рельсах от изгиба и кручения, кг;zг и zn – расстояние от горизонтальной нейтральной оси до крайних волокон соответственно головки и подошвы с учетом износа, см (см. табл. 1.3); bг и bn – ширина соответственно головки и подошвы рельса, см (см. табл. 1.3); 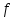 - коэффициент перехода от осевых напряжений к кромочным, - коэффициент перехода от осевых напряжений к кромочным, 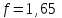 ; ;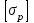 - расчетное допускаемое напряжение в рельса от поездной нагрузки, кг/см2. - расчетное допускаемое напряжение в рельса от поездной нагрузки, кг/см2.Максимально напряжение в прокладках на железобетонных шпалах σпр, кг/см2, определяется по формуле 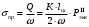 , (1.20) , (1.20)где ω – площадь подкладки, см2 (см. табл. 1.3). Максимально напряжение в балласте под шпалой σб, кг/см2, определяется по формуле 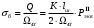 , (1.21) , (1.21)где Q – нагрузка на шпалу от рельса, кг; 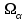 - площадь полушпалы с поправкой на изгиб, см2 (см. табл. 1.3); - площадь полушпалы с поправкой на изгиб, см2 (см. табл. 1.3);lш – расстояние между осями шпал, см (см. табл. 1.3); 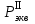 - максимальная эквивалентная нагрузка для расчетов напряжений в элементах подрельсового основания, кг. - максимальная эквивалентная нагрузка для расчетов напряжений в элементах подрельсового основания, кг. Полученные в результате расчета напряжения σпр и σб сравнивают с допускаемыми [σпр] и [σб]. Превышение расчетных максимальных напряжений в рельсах σп-к, σг-к над допускаемыми [σб] указывает на необходимость уменьшения скорости движения поездов по условию прочности пути. Превышение расчетных напряжений в прокладках железобетонных шпал и напряжений в балласте σпр и σб над допускаемыми [σпр] и [σб] указывает на необходимость усиления пути и улучшения его текущего содержания на таких участках. Превышение расчетных напряжений над допускаемыми в пределах 30 % не является причиной для уменьшения скорости движения поездов. Нормальные напряжения σh, кг/см2, в балласте на глубине h от подошвы шпалы по расчетной вертикали определяется по формуле 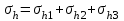 , (1.22) , (1.22)где 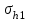 и и 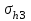 - напряжения от воздействий соответственно 1-й и 3-й шпал, лежащих по обе стороны от расчетной шпалы, кг/см2; - напряжения от воздействий соответственно 1-й и 3-й шпал, лежащих по обе стороны от расчетной шпалы, кг/см2;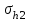 - напряжения от воздействий 2-й шпалы (расчетной) в сечении пути под колесом, кг/см2. - напряжения от воздействий 2-й шпалы (расчетной) в сечении пути под колесом, кг/см2.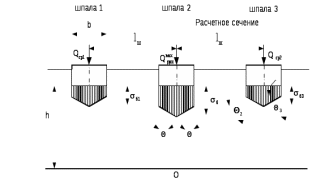 Рисунок 1.2 - Расчетная схема определения напряжений на основной площадке земляного полотна. Нормальное напряжение в балластном слое и на основной площадке земляного полотна определяются на глубине h от подошвы шпалы в сечении пути под расчетным колесом. Расчетное колесо располагается по направлению оси шпалы. Напряжение от воздействия 2-й шпалы (расчетной) в сечении пути под колесом, σh2, кг/см2, определяется по формуле 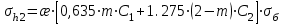 , (1.23) , (1.23)где æ – коэффициент, учитывающий неравномерность распределения давления вдоль шпалы и пространственность приложения нагрузки, для пути с железобетонными шпалами, æ = 0,7; m – переходный коэффициент от осредненного по ширине шпалы давления на балласт к давлению под осью шпалы, при m< 1 принимается m = 1, при m> 2 принимается m =2, 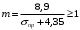 , (1.24) , (1.24)где С1, С2 – коэффициенты, зависящие от ширины нижней постели шпалы b и глубины h, для железобетонных шпал b = 27,5 см. 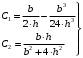 , (1.25) , (1.25) где σб – расчетное напряжение в балласте в подрельсовом сечении. 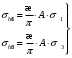 , (1.26) , (1.26)где А – коэффициент, учитывающий расстояние между шпалами lш, ширину шпалы b и глубину h. 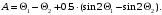 (1.27) (1.27)Углы 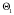 и и 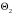 , радиан, определяются по формулам , радиан, определяются по формулам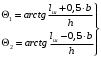 , (1.28) , (1.28)где 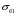 и и 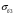 – средние значения напряжений по подошве соседних с расчетной шпалы, кг/см2. – средние значения напряжений по подошве соседних с расчетной шпалы, кг/см2.Напряжения в балласте под соседними с расчетными шпалами определяется из условия максимальной динамической нагрузки расчетного колеса, расположенного над расчетной шпалой, и средних нагрузок от остальных колес. 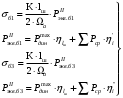 , (1.29) , (1.29)где ηlш– ордината линии влияния перерезывающей силы, при x=lш; 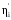 –ордината линии влияния перерезывающей силы, при x=l1+ lш; –ордината линии влияния перерезывающей силы, при x=l1+ lш;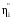 –ордината линии влияния перерезывающей силы, при x=l1–lш; –ордината линии влияния перерезывающей силы, при x=l1–lш;Для расчета верхнего строения пути на прочность принимаем вагоны 4-осные на тележках ЦНИИ-ХЗ. Характеристики 4-осного вагона приведены в таблице 1.4. Таблица 1.4 - Характеристики 4-осного вагона
Характеристика пути: Рельсы типа Р65 новые; шпалы железобетонные; эпюра шпал в кривой - 2000 шт/км; радиус кривой R = 412 м; балласт щебеночный, толщина под шпалой 0,40 м; толщина песчаной подушки 0,20 м. Расчетные параметры, необходимые для определения нагрузок на путь и напряжений в элементах верхнего строения пути сведены в таблице 1.5. Таблица 1.5 - Расчетные параметры верхнего строения пути
Окончание таблицы 1.5
Расчет: 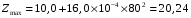 мм; мм;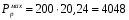 кг; кг;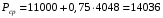 кг; кг;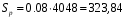 кг; кг;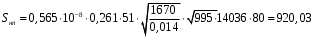 кг; кг;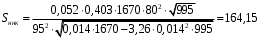 кг; кг;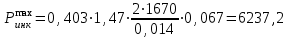 кг; кг;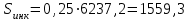 кг; кг;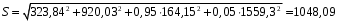 кг; кг;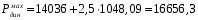 кг. кг.К= 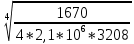 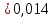 см-1 см-1 Таблица 1.6 - Значения и в зависимости от k li для 4х-oсного вагона
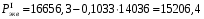 кг; кг;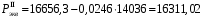 кг; кг; 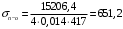 кг/см2; кг/см2;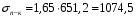 кг/см2; кг/см2;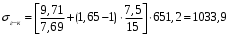 кг/см2; кг/см2;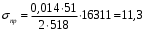 кг/см2; кг/см2;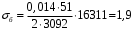 кг/см2. кг/см2.Полученные в результате расчета напряжения σпр и σб сравнивают с допускаемыми [σпр] и [σб]. В соответствии с [9] принимаем [σпр]=15 кг/см2, [σб] = 3 кг/см2. Данные расчетов не превышают допустимые значения следовательно в уменьшении скорости на данном участке в уменьшении скорости не требуется. Напряжения в балласте под шпалами определяются из условия максимальной динамической нагрузки расчетного колеса, расположенного над расчетной шпалой, и средних нагрузок от остальных колес. 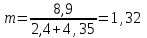 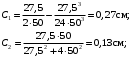 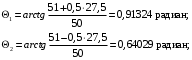 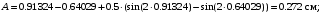 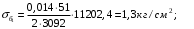 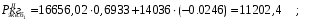 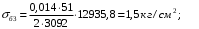 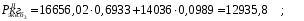 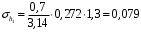 кг/см2; кг/см2;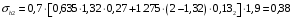 кг/см2; кг/см2;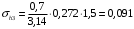 кг/см2; кг/см2;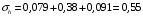 кг/см2. кг/см2.Т.к. полученные результаты не превышают максимально допустимых норм то данная конструкция пути соответствует всем нормам прочности пути и не требует каких-либо изменений. 1.2.3 Расчет коэффициента устойчивости против вкатывания гребня колеса на рельс При набегании колеса на рельс оно не должно накатываться своим гребнем на него, т.е. необходимо предотвратить вползание колеса на головку рельса. А если колесо окажется по некоторым причинам приподнятым, то необходимо, чтобы оно опустилось вниз.  Рисунок 1.3 – Расчетная схема определения устойчивости колеса на рельсе. Р1-ш и Р2-ш – нагрузка от кузова на шейки оси колесной пары; Р1-р – полная динамическая вертикальная нагрузка передаваемая от левого колеса на рельс A в точке O; Р2-р- правая динамическая вертикальная нагрузка, передаваемая от правого колеса на рельс B по кругу катания колеса; М1 и М2 – моменты, действующие на шейки оси; а1и а2 – расчетные консоли шеек оси; Yр – рамная сила; lр – расстояние от головки рельса до приложенной рамной силы; Jн – центробежная сила; Нц – расстояние от головки рельса до места приложения центробежной силы; F1 и F2 – силы трения гребня и поверхности катания колес по рельсам; N1 и N2 – реакции рельсов; S1 – расстояние между точками контакта колес с рельсами; Sш - расстояние между точками приложения сил к шейкам оси. Моменты действующие на шейки оси определяется по формуле 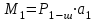 ; (1.30) ; (1.30)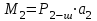 , (1.31) , (1.31)Вертикальные нагрузки на шейки оси от необрессоренной части экипажа определяется по формуле 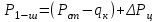 ; (1.32) ; (1.32)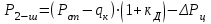 , (1.33) , (1.33)где Рст – статическая нагрузка колеса на рельс, Н; qк – отнесенный к колесу вес необрессоренной части экипажа, Н; кД – коэффициент динамики, кД=0,28 Динамическая рамная сила maxYр, приложенная на расстояние lр от точки контакта левого колеса с рельсом А. При этом обычно принимают, что 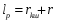 , (1.34) , (1.34)где rk – радиус колеса, м; rш – радиус шейки оси, м. У грузового вагона lр= 0,475+0,075=0,550, м. Сила трения гребня колеса по рабочей грани головки рельса определяется по формуле 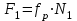 , (1.35) , (1.35)где N1 – нормальная к плоскости C-C реакция рельса А, кг; 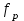 - коэффициент трения скольжения колеса по рельсу А. - коэффициент трения скольжения колеса по рельсу А.Реакция рельса А определяется по формуле 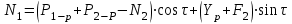 , (1.36) , (1.36)где N2 – вертикальная реакция рельса B, кг; F2 – сила трения бандажа колеса по поверхности катания головки рельса B, кг; 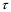 - угол горизонталью рабочей гранью головки рельса - угол горизонталью рабочей гранью головки рельса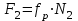 . (1.37) . (1.37)Реакция рельса В определяется по формуле 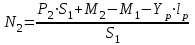 . (1.38) . (1.38)Коэффициент устойчивости против вползания колеса на рельс определяется отношением сил, препятствующим подъему колеса, к силам вызывающим этот подъем 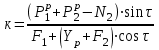 , (1.39) , (1.39)где Yр – рамная сила, кг. При расчетах можно принять угол τ между горизонталью и касательной к рабочей грани головки рельса в точке O касания гребня колеса с рельсом упорной нити для вагонов равным 600. У четырехосного грузового вагона lр = 0,55 м, а1 = 0,264 м, а2 = 0,168 м, fp = 0.25. Непогашенная часть центробежной силы, приходящаяся на одно колесо определяется по формуле 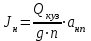 , (1.40) , (1.40)где g – ускорение силы тяжести, 9,81, м/с2; n – число осей экипажа; анп – непогашенное ускорение, м/с2; Qкуз – вес кузова брутто, кг 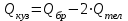 (1.41) (1.41)где Qбр – грузоподъемность, кг (для 4-осного полувагона Qбр=91500 кг); Qтел – вес тележки ЦНИИ-Х3, кг (Qтел=4650 кг) Дополнительная нагрузка определяется по формуле 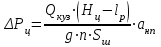 , (1.42) , (1.42)где Нц – расстояние от уровня головок рельсов до центра тяжести кузова (у груженого полувагона Нц = 2 м); Sш – расстояние между серединами шеек колесной пары ( у грузового полувагона Sш = 2,036 м); Полные расчетные нагрузки от колес на головки рельсов определяется по формулам 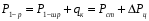 ; (1.43) ; (1.43)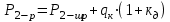 , (1.44) , (1.44)Величина непогашенного ускорения определяется по формуле 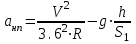 , (1.45) , (1.45)где V – скорость движения, км/ч; R – радиус кривой, м; h – возвышение наружного рельса, м; S1 – расстояние между осями рельсов, S1 = 1,6 м. Величину возвышения наружного рельса принимаем 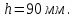 Расчет: 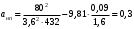 м/с2; м/с2;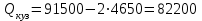 кг; кг;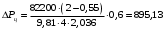 кг; кг;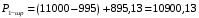 кг; кг;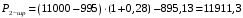 кг; кг;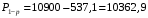 кг; кг;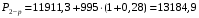 кг; кг;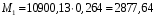 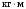 ; ;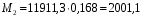 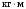 . .Определим реакцию рельса B при трех величинах рамной силы, при разных тормозных силах NT=0 кг; NT=70000 кг; NT=100000 кг 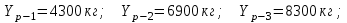  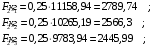 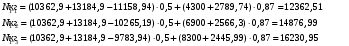 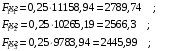  Поскольку устойчивость колеса грузового вагона гарантируется только при коэффициенте устойчивости к ≥ 1,3, а в данном случае режим торможения с тормозной силой 700 кН допустим, а с 1000 кН недопустим. Если же необходимо применение торможения силой 1000 кН, то для этого следует установить временное ограничение скорости. 1.2.4 Расчет устойчивости пути против поперечного сдвига Поперечный сдвиг рельсошпальной решетки под поездом является прямой угрозой безопасности движения поездов. При неблагоприятных сочетаниях воздействующих на путь вертикальных и горизонтальных поперечных сил может произойти поперечный сдвиг рельсошпальной решетки по балласту, особенно загрязненному или в талом состояние. 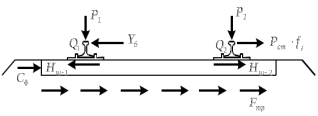 Рисунок 1.4 – Расчетная схема определения поперечной устойчивости пути. Р1 и Р2 – нагрузка от колеса на рельсы; Yб – боковая сила на упорный рельс; Q1 и Q2 – давление рельсов на шпалу; Нш-1 и Нш-z – поперечные силы, действующие на шпалу от двух рельсов; С0 – начальное сопротивление смещению шпалы; Fтр – сила трения шпалы по балласту; fр – коэффициент трения скольжения колеса по рельсу. Из расчета на прочность известно [2], что 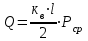 , (1.47) , (1.47)где кв – коэффициент относительной жесткости подрельсового основания и рельса,кв = 1,578, м-1; l – расстояние между осями шпал, м. Удерживающая от сдвига шпал сила – сопротивление их поперечному перемещению в балласте определяется по формуле 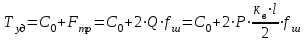 , (1.48) , (1.48)где С0 – начальное сопротивление смещению шпал при отсутствии вертикальной нагрузки, С0 = 200 кг; Fтр – сила трения шпалы по балласту при наличии вертикальной нагрузки, кг; 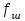 - коэффициент трения шпалы по балласту. - коэффициент трения шпалы по балласту.Поперечная сдвигающая сила является равнодействующей двух сил, приложенных к рельсам и определяется по формуле 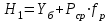 , (1.49) , (1.49)где fp – коэффициент трения скольжения колеса по рельсу, fp=0,25. Поскольку наибольшие боковые силы передаются, как правило, от первых направляющих колес, сила трения 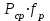 принимается со знаком минус. принимается со знаком минус.Поперечная сдвигающая сила Нш-1, действующая на шпалу от наружного рельса, и поперечная сила Нш-2, действующая на шпалу от второго (внутреннего) рельса и препятствующая сдвигу, определяется по формуле 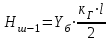 , (1.50) , (1.50)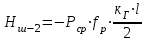 , (1.51) , (1.51)где кг – коэффициент относительной жесткости подрельсового основания и рельса в горизонтальной плоскости, м-1. 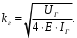 (1.52) (1.52)Суммарная сила, сдвигающая шпалу, определяется по формуле 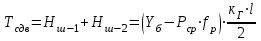 , (1.53) , (1.53)При торможении в кривой возникает дополнительная поперечная сила, которая определяется по формуле 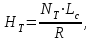 (1.54) (1.54)где Nт – тормозная сила, кг; Lc – расстояние между центрами автосцепок вагона, м. Коэффициент устойчивости пути против поперечного сдвига под поездом определяется отношением удерживающих и сдвигающих сил определяется по формуле 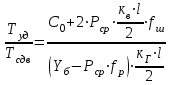 , (1.55) , (1.55)После сокращения на l / 2 формула примет вид 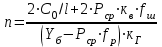 , (1.56) , (1.56)Рассмотрим случай предельного равновесия, т.е. примем n = 1. При этом получим 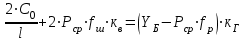 , (1.57) , (1.57)Отсюда видно, что путь под поездом с осевой нагрузкой Рср оказывается в предельном равновесии, если поперечная боковая сила достигает величины 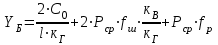 . (1.58) . (1.58)После деления левой и правой части на величину Рср получим предельно допустимое отношение поперечной боковой силы к вертикальной 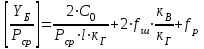 , (1.59) , (1.59)где fш – железобетонные шпалы на щебне, fш = 0,45. Путь можно считать устойчивым, если 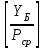 > >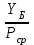 . .Расчет: 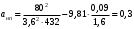 м/с2; м/с2;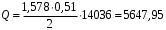 кг; кг;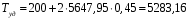 кг; кг;Величины боковых сил Yб при расчетном ускорении и тормозных силах NT=0; NT=70000 кг; NT=100000 кг 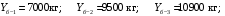 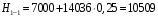 кг; кг;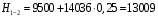 кг; кг;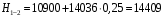 кг; кг;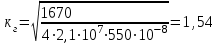 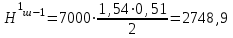 кг; кг;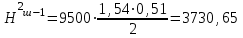 кг; кг;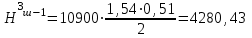 кг; кг;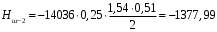 кг; кг;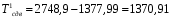 кг; кг;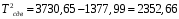 кг; кг;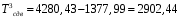 кг; кг;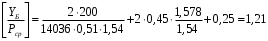 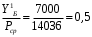 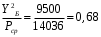 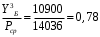 Проверка выполнения условия: Режим тяги NT= 0 кг: 0,52 < 1,21 – условие выполняется; Режим торможения NT=70000 кг: 0,71 < 1,21 – условие выполняется; Режим торможения NT= 100000 кг: 0,82 < 1,21 – условие выполняется. Так как условие 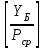 > > выполняется, то устойчивость пути против поперечного сдвига полностью обеспечивается. выполняется, то устойчивость пути против поперечного сдвига полностью обеспечивается.1.2.5 Расчёты напряжений в элементах верхнего строения пути от действия подвижного состава выполненные на ЭВМ По данным расчетов напряжений на ЭВМ (Прил. А) были построены графики зависимости модуля упругости подрельсового основания, от статической нагрузки на колесо (рис.1.5 и рис.1.6). Во всем диапазоне осевых нагрузок напряжения не превышают допускаемых, поэтому возможно применение рельсов типа Р65 на данном участке. Напряжения на шпале изменяется по линейному закону. Наибольшие напряжения не превышают допускаемых при данной грузонапряженности. Напряжения на балласте под шпалой и в уровне основной площадки также изменяются по линейному закону, наибольшие значения ниже допускаемых. Для снижения уровня величин напряжений рекомендуется укреплять основную площадку земляного полотна прослойками из мелкозернистого песка, сортированного гравия. По выполненному ручному расчету зависимости напряжений в балласте б, в шпале ш, в основной площадке h и в кромке подошвы рельса р близки к линейным. Напряжения возрастают с увеличением скорости, однако не превышают допускаемых. 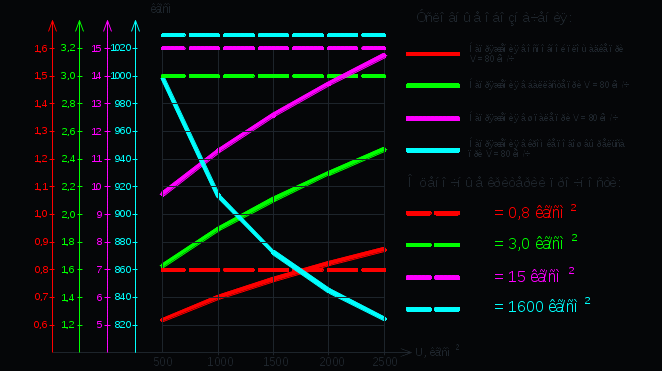 Рисунок 1.5 – Зависимость напряжения в элементах верхнего строения пути от модуля упругости при V=60км/ч 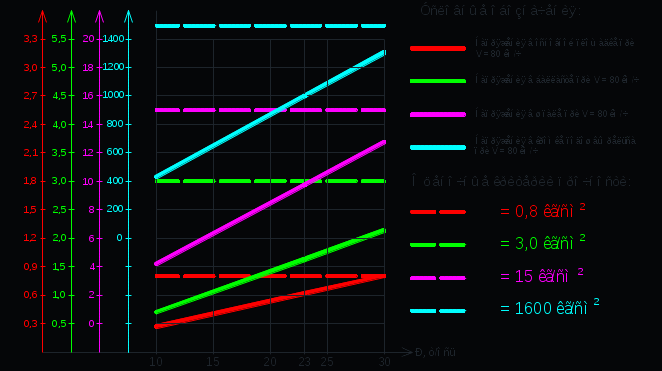 Рисунок 1.6 – Зависимость напряжения в элементах верхнего строения пути от статической нагрузки при V=60км/ч ВЫПРАВКА ПРОДОЛЬНОГО ПРОФИЛЯ И ПЛАНА ПУТИ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
