Практикум по АХ-2003,часть1. Практикум по аналитической химии в 2 ч. Учебное пособие. Ч. Омск Омский госуниверситет, 1998. 176 с
 Скачать 1.29 Mb.
|
6.3. РАСЧЕТЫ ПРОТОЛИТИЧЕСКИХ РАВНОВЕСИЙПрактическое занятие № 3 Для подготовки к данному практическому занятию необходимо проработать материал по учебникам, например [ 3, с.286-299; 4, с.30-66; 6,с.42-48 и др.]. Наиболее соответствует университетской программе учебное пособие [9, с.20-36 и 146-151]. В настоящем издании приводятся лишь важнейшие формулы и примеры расчетов. Теоретические сведенияДля разработки и сопоставления методик анализа необходимо уметь:
Все вышеуказанные расчеты требуют знания констант ионизации, т.е. взаимосвязанных констант кислотности Ka и констант основности Kb (иначе их называют кислотными и основными константами). При этом pKa + pKb = pKS, где KS - константа автопротолиза соответствующего растворителя. Значения констант зависят от природы растворенного вещества и растворителя, а также от температуры. На практике расчеты равновесий проводятся только для водных растворов и температуры 250С: для других растворителей и температур в справочной литературе не хватает данных по константам. Расчет pH растворов различного типа. Можно выделить следующие практически важные частные случаи: сильные кислоты (основания); слабые кислоты (основания); амфотерные вещества; смеси кислот (оснований); смеси, содержащие кислоту и ее сопряженное основание (буферные системы). В любом случае расчеты могут проводиться с разной степенью точности. Если высокая точность не требуется (а на практике она требуется довольно редко), пренебрегают влиянием ионной силы раствора и считают, что рН = - lg [H+]. Самоионизацией растворителя (воды) как рН-определяющим фактором обычно можно пренебречь, но, если концентрация растворенного вещества меньше 10-6 моль/литр или pK больше 12 единиц (для кислот pKa > 12, для оснований pKb >12), пренебрежение этим процессом уже недопустимо. При дальнейшем изложении общую концентрацию растворенного вещества (в моль/литр) обозначим символом С; будем считать, что все растворы - водные, их температура равна 250 С, а pKS = 14,0. Предполагается, что протолиз идет только по одной ступени, а последующими ступенями процесса можно пренебречь. В результате сделанных допущений расчет рН однокомпонентных систем становится очень легким: сильные кислоты: pH = pC (10) сильные основания: pH = pKs - pC (11) очень слабые кислоты: рН =  (12)очень слабые основания: pOH =  (13) амфотерные соединения: pH =  (14)Вывод соответствующих формул имеется в учебниках. Следует учесть, что в некоторых отечественных учебниках издания 60 - 80-х годов материал по кислотно-основным процессам рассматривается не с позиции протолитической теории, а с точки зрения теории электролитической диссоциации, что не только затрудняет вывод обобщенных расчетных формул, но и не соответствует современному уровню развития аналитической химии. Однако сами формулы и результаты расчетов по ним не зависят от того, какую именно теорию мы применяем для описания кислотно-основных процессов в водных растворах. Формулы (12) и (13) применимы, если степень протолиза соответствующих кислот или оснований меньше 1%. В этом случае величина pKa (для оснований - pKb) должна быть больше (pС + 2), однако она не должна превышать 10-12 единиц. Если вышеуказанные условия не выполняются, то для расчета pH требуется составление и решение системы уравнений (см. пример 3). При расчете рН смеси двух кислот (оснований) примерно одинаковой силы, имеющих близкие значения констант ионизации, можно пользоваться теми же формулами (10-13), подставляя в них суммарную концентрацию компонентов смеси. Если один из компонентов смеси является гораздо более сильной кислотой (основанием), чем второй, и их концентрации в растворе - величины одного порядка, то при ориентировочном расчете рН можно не учитывать вклад более слабого протолита. Если же различие в величине рК достоверно, но не очень велико (до 2 единиц), то расчет pH сильно осложняется, необходимо решать систему уравнений. При расчете рН буферной системы, содержащей одновременно кислоту HA и ее сопряженное основание A (в соизмеримых концентрациях), pH раствора приблизительно соответствует величине pH = pKa + lg  (15)В данную формулу подставляют молярные концентрации. Если в условии задачи концентрации выражены в других единицах, их необходимо перевести в молярные. Вместо отношения концентраций компонентов в этом расчете можно использовать отношение числа молей основания к числу молей кислоты. Необходимо помнить, что кислоту и основание в формуле (15) понимают обобщенно, в соответствии с теорией Бренстеда. Расчет состава буферного раствора. Изменение рН при добавлении реагентов. При выборе буфера для создания желаемого значения рН величина pKa буферной системы не должна отличаться от рН раствора более чем на одну единицу. В этом случае концентрации обеих форм растворенного вещества будут величинами одного порядка (различаться не более чем в 10 раз) и буфер будет в одинаковой мере устойчив по отношению к добавляемым кислотам и основаниям. Кроме того, следует учитывать другие требования к компонентам буферной системы (химическая инертность, растворимость, безопасность, доступность, низкая стоимость). Если один из компонентов буфера мало доступен, на практике берут другой компонент в концентрации С0 и частично переводят его в сопряженную форму, добавляя сильную кислоту или щелочь до необходимого значения рН. Величину рН в ходе прибавления реагента контролируют с помощью рН-метра. Например, аммиачный буфер обычно готовят из хлорида аммония и аммиака, но можно готовить его и другими способами: а) частично нейтрализуя аммиак соляной кислотой; б) подщелачивая до нужного рН раствор хлорида аммония едким натром. Равновесные концентрации каждого из компонентов буферной системы следует рассчитывать по уравнению (15), дополнив его условием CHA + CA = C0, где C0 - общая концентрация буферного раствора. Она выбирается аналитиком заранее с учетом того, какая буферная емкость требуется. Чем больше С0, тем более устойчив будет буфер по отношению к добавке посторонних кислот и оснований, т.е. тем менее будет отличаться величина рН раствора, полученного при их добавлении (далее обозначается pH*), от исходного значения рН. Величину рН* лучше рассчитывать не по формуле (15), включающей концентрации компонентов буфера, а по равносильной ей формуле рН* = рКа + lg 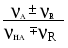 , (15а)где  и  - числа миллимолей кислотной и основной форм буфера в исходном растворе:  - число миллимолей реагента (сильной кислоты или основания) добавляемого в уже приготовленный буфер. Знак + или - ставится в зависимости от того, что именно (кислота или основание) добавляется в буфер (см. пример 9).Состояние вещества в растворе в зависимости от рН. Многие вещества могут находиться в растворе в виде равновесной смеси разных по своей протонированности форм, причем доля каждой формы зависит от рН раствора. Мольные доли форм могут быть вычислены по сравнительно несложным формулам, в которые входят значения кислотных констант для соответствующих протолитических переходов. Так, если вещество типа аммиака или уксусной кислоты может находиться только в двух формах (НА и А), а равновесие между ними характеризуется константой Ка, то: НА =  =  ; A = =  ; (16)Для вещества, которое в растворе может находиться в трех формах (типа угольной кислоты или этилендиамина): Н2А = 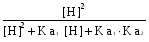 НА = 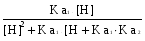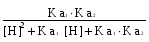 А =  . (16а)Аналогичные формулы можно вывести и для более сложных случаев. В этих формулах Ка1 соответствует отщеплению первого протона от наиболее протонированной формы, Ка2 соответствует отщеплению второго протона и т.д. Взаимные превращения сопряженных форм наглядно иллюстрируются на ионной диаграмме. В тех случаях, когда числовые значения констант сильно различаются (на 2 порядка и более), при расчете мольной доли формы, доминирующей при данном рН, можно учитывать не все константы, а только те, которые характеризуют переход этой формы в сопряженные с ней («соседние» на ионной диаграмме). Так, при расчете мольной доли молекул Н3РО4 при рН 2 рекомендуется учитывать только процесс перехода этих молекул в однозарядные анионы Н2РО4–, т.е. считать фосфорную кислоту одноосновной и применять формулу (16). Дальнейшим депротонированием можно пренебречь, поскольку рКа2 = 7,21. Даже без построения ионной диаграммы видно, что при рН 2 молекулы Н3РО4 доминируют, довольно много в растворе и анионов Н2РО4–, другие же формы фосфатов практически отсутствуют. При построении ионных диаграмм следует помнить, что наиболее протонированная форма вещества доминирует в растворе при рН < pK1; следующая - при рН от рКа1 до рКа2, и т.д. Наименее протонированная форма А доминирует при значениях рН, больших числового значения показателя последней константы. При построении ионных диаграмм рекомендуется использовать программу «Протолиз». Примеры расчетов1. Рассчитать pH 0,4 % -го раствора едкого натра. Решение. Переведем процентную концентрацию в молярную: в 1 литре данного раствора содержится 4 г едкого натра (плотность раствора считаем равной единице), т.е. 0,1 моль. Каждому молю гидроксида натрия (сильного основания) соответствует один моль гидроксид-ионов, следовательно, концентрация их в растворе также будет равна 0,1 М. Применим формулу (11): pOH = - lg 0,1 = 1; pH = 14 - pOH = 14 - 1 = 13. 2. Рассчитать pH 0,01 М раствора цианида натрия. Решение. Цианид натрия - основание, так как катионы натрия протолизу не подвергаются, а цианид-ионы связывают протоны, образуя слабую синильную кислоту. По справочнику находим pKa для перехода HCN / CN– = 9,21. Рассчитываем значение pKb цианида: = 14 - 9,21 = 4,79. Для данного раствора pC = - lg0,01 = 2,0. Выполняется условие pKb > pC +2, т.е. цианид можно считать очень слабым основанием. Расчет производим по приближенной формуле (13): pOH =  = 0,5 (4,79 + 2,0) 1,7 ; pH = 14 - pOH = 12,3.3. Рассчитать pH 0,001 М раствора муравьиной кислоты. Решение. По справочнику находим pKa = 3,8, кислота слабая, pC = - lg 0,001 = 3, условие pKa > pC +2 не выполняется, считать по приближенной формуле нельзя. Составляем уравнение: HA = H + A (заряды опускаем) Ka =  =  . Отсюда [H] = -Ka/2 +  = -10-3,8/2 +  3,3· 10-4;pH = -lg 3,3.10-4 = 3,48 (3,5. При вычислении рН по упрощенной формуле мы получили бы значение pH = 3,4. 4. Вычислить pH 0,01 % -го раствора гидрокарбоната натрия. Решение. Гидрокарбонат-ион может как отдать протон (превращаясь в карбонат), так и принять его от молекулы воды, превращаясь в угольную кислоту. Поэтому гидрокарбонат- ион следует считать амфотерной частицей, а в растворе одновременно находятся все три формы угольной кислоты. Для угольной кислоты в справочнике находим: pKa1 = 6,35 (переход Н2СО3 / HCO3), pKa2 = 10,32 (переход НСО3 / CO3). Общая концентрация карбонатов в данном случае значения не имеет. Расчет производится по формуле (14): pH = 0,5 (6,35 + 10,32) = 8,34. 5.Рассчитать pH 0,01 М раствора серной кислоты. Решение. Запишем уравнение диссоциации серной кислоты: H2SO4 = 2H+ + SO42–. Серная кислота - сильная, в водном растворе она подвергается 100 %-му протолизу по первой ступени, а степень протолиза по второй ступени также близка к 100%, следовательно, в растворе концентрация ионов водорода равна молярной концентрации кислоты, умноженной на 2, т.е. 0,02 и pH = - lg 0,02 = 1,7. Более точный расчет, учитывающий неполный протолиз по второй ступени, дает величину рН 1,8. 6. Рассчитать pH 0,1 М HCl в присутствии 0,01 моль/л сульфата алюминия. Решение. HCl - сильная кислота, в растворе полностью подвергается протолизу (диссоциирует), следовательно, [H+] = CHCl = 0,1. Но в растворе присутствует значительное количество сильного многозарядного электролита - Al2(SO4)3, и активность ионов водорода значительно отличается от концентрации. Рассчитаем ионную силу раствора: I [Al2(SO4)3] = 0,5 (0,02·32+ 0,03·22) = 0,15. Следует учесть ионную силу, создаваемую самой хлористоводородной кислотой. Для нее I = СHCl = 0,1. Общая ионная сила раствора, таким образом, равна 0,25. При такой ионной силе коэффициент активности однозарядных ионов водорода лучше взять по справочнику [8, с.87]: fH = 0,80. Поэтому активность Н+– ионов равна 0,080, а pH 1,1. 7. Рассчитать pH раствoра, в 150 мл которого имеется 15 г KCN и 10 г HCN. Решение. Раствор содержит одновременно слабую кислоту и ее сопряженное основание - цианид-ионы. С учетом молярных масс компонентов вычисляем молярные концентрации компонентов буфера: [HCN] = 2,47 (моль/л); [KCN] = 1,54 (моль/л). Применяя формулу (15) для вычисления pH буферных растворов, получим pH = pKa + lg 1,54 / 2,47 = 9,21 - 0,21 = 9,00. 8. Требуется приготовить 2 л 0,25 М буферного раствора с pH 5,0. Предложить методику приготовления такого буфера. Решение. Выбираем сопряженную пару «кислота - основание» (по Бренстеду) так, чтобы pH буфера отличался бы от pKa пары менее чем на единицу. По таблице констант ионизации находим кислотно-основную пару, удовлетворяющую этому условию: для перехода HAc / Ac– значение pKa = 4,74, причем компоненты буфера (уксусная кислота и ее соли) достаточны инертны, растворимы и доступны. Расчет проводим по формуле (15), но заменяя в ней отношение концентраций отношением числа молей обеих форм: pH = pKa + lg Ac /HAc. Так как в 2 л 0,25 М буфера содержится 0,50 моля суммы (HAc + Ac-): Ac + HAc = 0,50 ; pH = 5 = 4,74 + lg (0,5 - Hac) / HAc. Отсюда после простых преобразований получается HAc = 0,177; Ac- = 0,5 - 0,177 = 0,323. Переведем число молей HAc и Ac- в массы: mHAc = Hac. MHAc = 0,177 · 60,0 = 10,6 (г); mNaAc = Ac. MNaAc = 0,323 · 82,0 = 26,5 (г). Для приготовления буфера необходимо взять 10,6 г ледяной уксусной кислоты и 26,5 г ацетата натрия, растворить в воде и довести объем раствора до 2 л. 9. Как изменится pH одномолярного аммиачного буфера с pH = 9, если к 150 мл его прилить 20 мл 5%- й соляной кислоты? Решение. При протекании в среде буфера реакций, сопровождающихся выделением или связыванием протонов, величину рН* следует рассчитывать по формуле (15а). Перед основным расчетом вычислим первоначальное число молей компонентов буфера (до введения HCl), а также число молей НСl. Буфер одномолярный, т.е. [NH3] + [NH4] = 1; Взято 150 мл буферного раствора: [NH3] + [NH4] = 0,15. Из условия задачи известно первоначальное значение pH: 9 = 9,26 + lg [NH3] / [NH4] = 9,26 + lg (0,15 - [NH4]) / [NH4]). Решая последнее уравнение, получим (0,15 - [NH4])/[NH4] = 0,55; [NH4] = 0,097; [NH3] = 0,15 - 0,097 = 0,053. В 20 мл 5%-й HCl содержится 20·0,05 = 1 г хлористого водорода, т.е. 1/36,5=0,027 моль. Плотность раствора HCl приняли равной единице. Подставляя найденные величины в формулу (15а), получаем: рН* = 9,26 + lg  = 8,28, что и требовалось определить по условию. Можно было построить следующую цепочку рассуждений (начинающим такой вариант решения понятнее): При приливании кислоты к буферному раствору идет реакция: H+ + NH3 = NH4+, т.е. расходуется 0,027 моль NH3 и образуется 0,027 моль NH4+. После реакции в растворе окажется 0,053 - 0,027 = 0,026 моль NH3. Ионов аммония окажется 0,097 + 0,027, т.е. 0,124 моль. Величину pH полученного раствора рассчитываем по обычной формуле: pH = 9,26 + lg 0,026/0,124 = 8,58. Естественно, под действием добавленной соляной кислоты произошло снижение рН буферного раствора, но сдвиг рН относительно невелик - с 9 до 8,6. 10. Составить ионную диаграмму, описывающую состояние пирофосфорной кислоты в водном растворе. Решение. Поскольку кислота имеет формулу H4P2O7 и может находиться в водном растворе в пяти различных формах (молекулы Н4R и анионы H3R; H2R; HR; R, отличающиеся друг от друга не только протонированностью, но и зарядом), необходимо построить пять кривых, изображающих графическую зависимости мольной доли соответствующей формы от рН. Таким образом, диаграмма строится в координатах % = f (pH). При pH = 0 выход молекулярной формы близок к 100%, а по мере повышения pH падает из-за перехода молекул в анионы H3R-. Содержание этих ионов постепенно возрастает с ростом рН, а затем снижается, по мере перехода их в ионы H2R, и т.д., вплоть до сильно щелочной среды, где доминируют анионы R4-. Для построения кривых необходимо найти в справочниках кислотные константы, соответствующие переходам между формами разной протонированности, Их показатели равны: 0,91; 2,10; 6,70;: 9,32. Из формулы расчета рН буферного раствора следует, что величина pH равна pKa. при [Кисл.] = [Осн], что соответствует пересечению кривых на ионной диаграмме. Доля каждой из сопряженных форм при этом рН составляет около 50% (если пренебречь наличием других форм кислоты). Очевидно, молекулы Н4R доминируют при рН < 0,91. Анионы H3R- доминируют при рН от 0,91 до 2,10, причем максимальный выход их, приближающийся к 100%, будет на середине интервала (при рН 1,5) и т.д. Таким способом можно получить ионную диаграмму в целом, хотя нельзя достичь высокой точности. 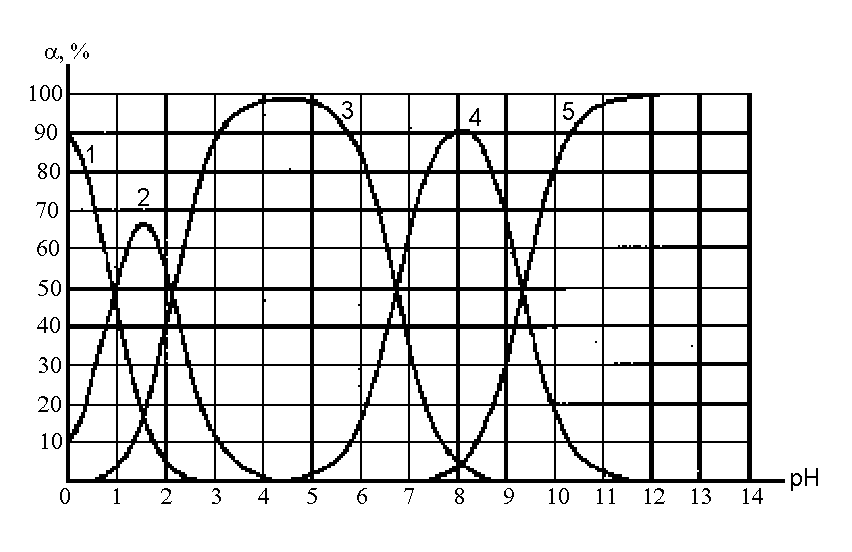 С помощью компьютера можно построить диаграмму гораздо точнее. Программа PROTOLIZ рассчитывает -функции при разных рН. Результат расчета показан на рис.1. Рис.1. Ионная диаграмма, показывающая состояние пирофосфорной кислоты в водном растворе 1 – H4R; 2 – H3R-; 3 – H2R2-; 4 - HR3-; 5 – R4- 11. В каких формах при pH = 10 находится сероводород в водном растворе? Рассчитать мольные доли каждой из форм. При каком рН достигается максимальный выход гидросульфид-анионов? Решение. Сероводородная кислота - двухосновная, в растворе она всегда существует в трех формах: H2S, HS- и S2-. Значения показателей кислотных констант (округленно): pKa1 = 7,0; pKa2 = 12,6. Следовательно, в растворах с рН от 7,0 до 12,6 (в том числе и при рН 10) доминирует форма HS-. Доли всех форм рассчитаем по формулам (16а): Н2S =  0,001; HS =  0,996;S =  0,003.Наивысший выход гидросульфидов в середине их зоны доминирования, т.е. при рН = (7,0 + 12,6) / 2 = 9, 8. Контрольные вопросы1. Какие соединения с точки зрения протолитической теории являются кислотами, основаниями, амфотерными соединениями? Дайте примеры молекулярных, анионных и катионных кислот (оснований). Что такое протолиз и автопротолиз? 2. Что называется водородным показателем раствора, как эта величина рассчитывается и измеряется? 3. Почему одно и то же значение рН в среде разных растворителей может соответствовать либо кислой, либо щелочной среде ? Дайте определение, какие растворы считаются кислыми, нейтральными, щелочными. 4. Почему шкала рН для водных растворов обычно соответствует интервалу от 0 до 14, а для растворов, выходящих за эти границы, понятие рН практически не применяется? Какие значения рН могут иметь растворы, приготовленные на основе других протолитических растворителей? 5. Какие факторы обычно учитываются при расчете рН растворов и какими принято пренебрегать? 6 В каких случаях при расчете рН можно пренебречь автопротолизом растворителя как источником Н+ -ионов, и в каких это приведет к серьезным ошибкам? 7. Дайте определение константам кислотности и основности. Как связаны их величины? Как меняется (при прочих равных условиях) величина рКа ряда растворенных протонсодержащих веществ, если прочность связи протона с остальной частью молекулы в этом ряду постепенно ослабляется? 8. Пользуясь справочником, укажите, какой катион в водном растворе будет иметь наиболее кислотный характер: аммоний, пиридиний, Pb2+. 9. Как можно создать в растворе заданное значение рН (дайте несколько вариантов ответа), будет ли это значение рН меняться при разбавлении раствора и добавлении к нему посторонних веществ? 10. Предложите несколько вариантов приготовления раствора с рН 8,0. 11. Что такое ионная диаграмма, в каких координатах она строится, в каких случаях аналитик использует такие диаграммы? 12. От каких факторов и как именно зависит мольная доля наиболее протонированной формы растворенного в воде вещества? |