Практикум по АХ-2003,часть1. Практикум по аналитической химии в 2 ч. Учебное пособие. Ч. Омск Омский госуниверситет, 1998. 176 с

• Название: Практикум по аналитической химии в 2 ч. Учебное пособие. Ч. Омск Омский госуниверситет, 1998. 176 с
• Анкор: Практикум по АХ-2003,часть1.doc
• Дата: 27.02.2018
• Размер: 1.29 Mb.
• Имя файла: Практикум по АХ-2003,часть1.doc
• Тип: Практикум; #16002
• страница: 15 из 27

6.4. РАСЧЕТЫ РАВНОВЕСИЙ КОМПЛЕКСООБРАЗОВАНИЯ

Практическое занятие № 4

Теоретические сведения

Константы устойчивости. Реакции комплексообразования в растворах используются при выполнении анализов в следующих случаях:

• 
  для обнаружения или маскирования растворенных веществ;
  
• 
  для перевода определяемого компонента в новое соединение (интенсивно поглощающее свет, люминесцирующее, экстрагируемое и т.д.);
  
• 
  для целенаправленного регулирования химических свойств определяемого вещества или реагента (кислотно-основных, окислительно-восстановительных и других, а также для изменения растворимости осадков);
  
• 
  для титрования ионов металла реагентами-лигандами (или наоборот).
  

Во всех этих случаях для выбора подходящего реагента, поиска оптимальных условий проведения реакции, оценки селективности и точности соответствующей методики анализа необходимо проводить расчеты с применением констант устойчивости (или констант нестойкости). В частности, так рассчитывают закомплексованность центрального иона, степень образования разных комплексов и другие равновесные характеристики [ см. 4, с.69-73 ]. Для проведения точных расчетов требуется информация о составе и прочности всех комплексов, которые могут образоваться в данной системе; кроме большого количества труднодоступных справочных данных, этот способ требует применения компьютеров и специального программного обеспечения.

Можно ограничиться предположением о существовании в растворе лишь одного - наиболее прочного - комплексного соединения. Пренебрежение ступенчатым характером комплексообразования позволяет быстро и легко получать ответ (пример 1), но иногда приводит к серьезным погрешностям. Во многих случаях этим способом вообще нельзя пользоваться; например, если в данной системе получается ряд комплексов, близких по своей прочности, или при образовании малопрочных соединений. В настоящем пособии преимущественно используются расчеты без упрощений, т.е. учитывается ступенчатый характер комплексообразования.

Обозначим через [M] равновесную концентрацию центрального иона (обычно катиона металла); [L] - равновесную концентрацию свободного лиганда, [ML], [ML₂], [ML₃] и т.д. (в общем случае [ML_i]) - равновесные концентрации соответствующих комплексов; все концентрации выражены в моль/литр. Пусть n - максимальное число лигандов L, которое с учетом их дентатности может присоединиться к М. Пренебрегая возможным образованием смешанных и многоядерных комплексных соединений, наличием во внутренней координационной сфере М молекул растворителя, постепенно вытесняемых лигандом L, запишем схему ступенчатого комплексообразования между М и L, а также выражения для соответствующих ступенчатых (K) и общих () констант устойчивости:

M + L  ML; K₁ = ; ₁ = ;

ML + L  ML₂; K₂ = ; ₂ = ;

ML₂ + L  ML₃; K₃ = ; ₃ = .

и так далее, вплоть до образования ML_n. В общем случае для i-ого комплекса

Ml_i-1 + L  ML_i ; K_i = ; _i = . (17)

При этом общие и ступенчатые константы связаны:

_i = K₁. K₂...... K_i. (18)

Удобнее считать по формуле:

lg _{i =} lg K₁ + lg K₂ +..... + lg K_i. (19а)

Если в справочнике даны лишь значения lg _i, то ступенчатые константы можно легко найти по разности:

lgKi = lg _i - lg _i-1. (19б)

Константы нестойкости представляют собой обратные значения констант устойчивости. Очевидно, для любой ступени процесса

k _нест = 1 / K_уст, pk _нест = lgK _уст. (20)

К _нест(общая) = 1/_уст, pK _нест = lg _уст. (20а)

Несмотря на то, что константы нестойкости широко представлены в справочниках и других книгах, изданных до 1975 г., пользоваться ими теперь не рекомендуется.

В ходе расчетов комплексообразования применяют (в том числе в настоящем пособии) концентрационные константы, однако их значения можно без большой погрешности брать прямо из справочников, где константы соответствующих равновесий приведены для нулевой или некоторой другой известной величины ионной силы. Дело в том, что ионная сила довольно слабо влияет на равновесие комплексообразования.

Расчет концентрации свободных ионов металла в отсутствие избытка лиганда

При решении таких задач допускают, что распад комплекса идет не ступенчато, а в одну стадию, например

Fe(CN)₆^3-  Fe³⁺ + 6 CN^-.

Из уравнения диссоциации комплекса видно, что [CN] = 6[Fe], поскольку в раствор не добавляли избыточных количеств цианида или железа (III). Обозначим начальную концентрацию комплекса - С, равновесную концентрацию свободных катионов железа [Fe] = x, а равновесную концентрацию комплекса как (С - x). Затем подставим данные в выражение общей константы устойчивости цианидного комплекса:

₆  (С - х) / х·(6х)⁶ = 10 ^43,9.

По этому уравнению можно найти х при любой начальной концентрации С. При С>>x для решения следует провести предварительное логарифмирование.

Расчеты закомплексованности и маскирования при введении избытка лиганда

Закомплексованность центрального атома М (комплексо-образователя) - столь же важная для практики величина, как растворимость осадка или кислотность буферного раствора. Закомплексованностью (Ф) называется отношение общей концентрации металла М (или другого вещества, выступающего в роли комплексообразователя) к концентрации не связанных в комплекс ионов М («свободного металла»). Закомплексованность является безразмерной величиной и принимает значения от 1 до . Чем больше значение Ф, тем ближе к 100 % выход комплексных соединений в данной системе, тем прочнее и полнее замаскирован свободный металл. Закомплексованность определяется природой М и L, температурой раствора и типом растворителя, она сильно зависит от концентрации свободного лиганда и практически не зависит от других факторов, в том числе от общей концентрации М в растворе⁵. Легко показать, что при избытке L:

Ф = = 1 + ₁ [L] + ₂ [ L ] ² +.... + _n [ L ] ⁿ. (21)

Поскольку в справочниках обычно приводятся не сами константы устойчивости, а их логарифмы, формулу (21) удобнее использовать в следующем виде:

Ф = 1 + . (21а)

Классическим примером является расчет взаимодействия железа (III) с роданид-ионами. Подставляя известные значения логарифмов констант устойчивости всех шести железороданидных комплексов из [8] в формулу (21а), получаем для 0,1 M по роданиду растворов (pL=1) следующее выражение для закомплексованности

Ф = 1 + 10^3,03-1 + 10^4,33-2 + 10^4,63-3 + 10^4,53-4 + 10^4,23-5 + 10^{3,3 -6} =

= 1 + 107 + 214 + 42,6 + 0,2 + 0,002 368; lg Ф = 2,57.

При установившемся равновесии величиной, обратной закомплексованности, является мольная доля свободного металла (_M):

_M = 1 / Ф = ; p_{M =} lg Ф. (22)

Так, мольная доля свободных ионов железа в растворе, децимолярном по роданиду, составляет всего 1/ 368 = 2,7·10^-3 или 0,27% от суммарной концентрации всех форм железа (III) в растворе. В сантимолярном растворе роданида закомплексованность гораздо меньше (пример 2). И наоборот, с переходом к одномолярным по роданиду растворам закомплексованность железа возрастает до 1,2· 10⁴, а доля свободного железа соответственно падает до величины, меньшей 0,01 %.

Формула (21) не только показывает, что для достижения большей закомплексованности требуется вводить избыток свободного лиганда, но и позволяет подбирать концентрацию лиганда, обеспечивающую заданную степень закомплексованности (пример 3). Расчет по формуле (21) относительно неизвестного [L] потребует решения уравнения высокой степени, что не всегда возможно без ЭВМ. Для некоторых систем, наиболее важных при маскировании металлов, такие расчеты проведены заранее. Соответствующие значения lgФ для нескольких целочисленных значений pL приведены в научной литературе, а также в приложениях к данному пособию. Эти значения используются в качестве поправок p_M при расчетах условных констант, например в комплексонометрии, однако в случаях, когда лиганд способен и к реакциям протолиза, расчет поправок осложнен необходимостью учитывать рН раствора.

Если пренебречь ступенчатым характером комплексообразования и считать, что в растворе образуется только комплекс ML_n, то формула (21) упрощается

Ф 1 + _n [ L ] ⁿ, (21б)

При _n[L]ⁿ >> 1, получается простая формула для приближенных вычислений

Ф  _n [ L ] ⁿ. (21в)

Концентрация лиганда L, обеспечивающая необходимую степень маскирования металла, в этом случае легко вычисляется без компьютера:

[ L ]  . (23)

Вопрос о том, какая степень маскирования М потребуется в каж-дом конкретном случае, решается заранее на основании исследования равновесия предотвращаемой реакции (например, реакции осаждения). Так, если требуется установить, сколько аммиака надо ввести в раствор, чтобы медь (II) оставалась в растворе в виде аммиачного комплекса и не выпадала в осадок в виде гидроксида, то вначале рассчитывают, при какой концентрации свободных ионов меди осадок Cu(OH)₂ в указанных условиях не выпадает, затем считают закомплексованность и находят равновесную концентрацию аммиака, обеспечивающую такую закомплексованность, по формулам (21) или(23), как в примере 4, а уже потом рассчитывают, сколько миллилитров концентрированного аммиака следует добавлять к раствору соли меди, чтобы создать соответствующую равновесную концентрацию молекул аммиака.

Определение степени образования различных комплексов в их смеси

Чтобы найти _i - мольную долю любого комплекса в их равновесной смеси, следует разделить на Ф соответствующее слагаемое в формулах (21) или (21а). Доля комплекса ML составляет ₁ [L] / Ф, доля комплекса МL₂ - ₂ [L]² / Ф и т. д. В общем случае

i = _i [L]ⁱ / Ф. (24)

Например, в 0,1 M по роданиду растворе соли железа, где мольная доля свободного железа была всего 0,0027, доля комплекса Fe(SCN)⁺⁺ равна 107:368=0,291; доля комплекса Fe(SCN)₂⁺ равна 214:368= 0,580 и т.д. Самое большое слагаемое в формуле (21a) соответствует доминирующему комплексу. Естественно, при переходе к другой концентрации свободного лиганда мольные доли всех комплексов изменяются и в новых равновесных условиях, возможно, будет доминировать другой комплекс. Более детально этот вопрос рассмотрен при решении примера 5.

В литературе описаны и способы решения обратной задачи - нахождения интервала концентраций лиганда, обеспечивающих доминирование комплекса заданного состава, но эти расчеты значительно сложнее и выходят за рамки базового курса аналитической химии. В настоящем пособии такие расчеты не рассматриваются. Решение можно найти в других книгах, например [17-18]. В ходе этих расчетов используются не общие, а ступенчатые константы устойчивости (или нестойкости).

Примеры решения типовых задач

1. Рассчитать концентрацию ионов Ag⁺ в растворе, где равновесная концентрация молекул NH₃ равна 0,1 моль/л, а общая концентрация серебра (I) - 0,001 моль/л.

Решение. Первый способ (см. [1]). Известно, что серебро связывается аммиаком в основном в комплекс состава 1:2. Запишем уравнение реакции:

Ag⁺ + 2NH₃  Ag(NH₃)₂⁺;

₂ = = 10^7,24 ;

С_Ag = 0,001; [NH₃] = 0,1.

В алгебраическом выражении константы устойчивости комплекса две величины неизвестны. Одну из них - [Ag] - необходимо найти по условию задачи, ее обозначим как x. Вторую же - [Ag(NH₃)₂] - можно рассчитать из уравнения материального баланса:

C_Аg = [Ag] + [Ag(NH₃)] + [Ag(NH₃)₂],

откуда [Ag(NH₃)₂] = C_Аg - [Ag] - [Ag(NH₃)].

Пренебрегая концентрацией неустойчивого промежуточного комплекса состава 1:1 (т.е. ступенчатым характером комплексообразования), получаем:

[Ag(NH₃)₂ ]  C_Аg - [Ag] = 0,001 - х.

Найденное выражение подставляем в уравнение константы

(0,001 - х) / х · 0,1² = 10^7,24.

Полученное уравнение содержит только одну неизвестную величину и легко решается. Решение можно еще больше упростить, если заметить, что комплекс довольно прочен, C_Аg >> [Ag], следовательно:

0,001 - х  0,001 0,1 / х  10^7,24 х = 10^{- 8,24}, [Ag]6·10^-9 моль/л.

Второй способ. Рассчитаем закомплексованность серебра в аммиачные комплексы без упрощений, по формуле (21а):

Ф = 1 + 10^3,32·10^-1 + 10^7,23·(10^-1)² = 1 + 10^2,32 + 10^5,23 = 1 + 209 + 169824 =

= 170234  1,7·10⁵

[Ag] = C _Ag / Ф = 0,001 / 1,7·10⁵  6·10 ^-9 (моль/ литр).

Судя по соотношению слагаемых при расчете закомплексованности, в данных условиях выход комплекса 1:2 почти на 3 порядка больше, чем комплекса 1:1, следовательно, концентрацией ненасыщенного комплекса в предыдущем варианте решения действительно можно было пренебречь.

Третий способ. Очевидно, [Ag] = C_Аg / Ф. Следовательно, lg[Ag] = = lg C_Аg - lg Ф. Величина lgC_Agпо условию равна -3. По таблице поправок на маскирование (приложение 6) находим, что для серебра в 0,1 М аммиачном растворе lgФ = 5,2. Подставляем эти величины в выведенную формулу:

lg [Ag] = -3-5,2 = -8,2 [Ag]  6·10 ^-9 (моль/ литр).

Oчевидно, этот способ формален. Второй способ для начинающих предпочтительнее.

2. Вычислить мольную долю комплекса FeSCN²⁺ в растворе, где общая концентрация роданида калия равна 0,01 М, а железа(III) - 10^-4 M.

Решение. Расходом роданида на связывание железа в комплексы пренебрегаем (это справедливо, если С_SCN >> C_Fe), тогда [SCN]=0,01 моль/л, рSCN = 2,0. Для железа (III) известно шесть роданидных комплексов: FeSCN²⁺; Fe(SCN)₂⁺;..... Fe(SCN)₆^3-. По справочнику [8] общие константы устойчивости этих комплексов имеют значения логарифмов, соответственно равные 3,03; 4,33; 4,63; 4,53; 4,23; 3,23. Для расчета общей закомплексованности нужно только подставить эти значения в формулу (21а), а для вычисления степени образования монороданидного комплекса взять из этой формулы соответствующее слагаемое и разделить его на общую закомплексованность. Такой вариант быстрее, чем подстановка данных в формулу (24).

Ф=1+10 ^{lgi - ipL} =1+10^3,03-2+10^4,33-4+10 ^4,63-6 +10 ^4,53-8 +10 ^4,23-10 +10 ^3,23-12 =

= 1 + 10^1,03 + 10^0,33 + 10^-1,37 + 10^-3,47 + 10^-5,77 + 10^-8,77 13,9.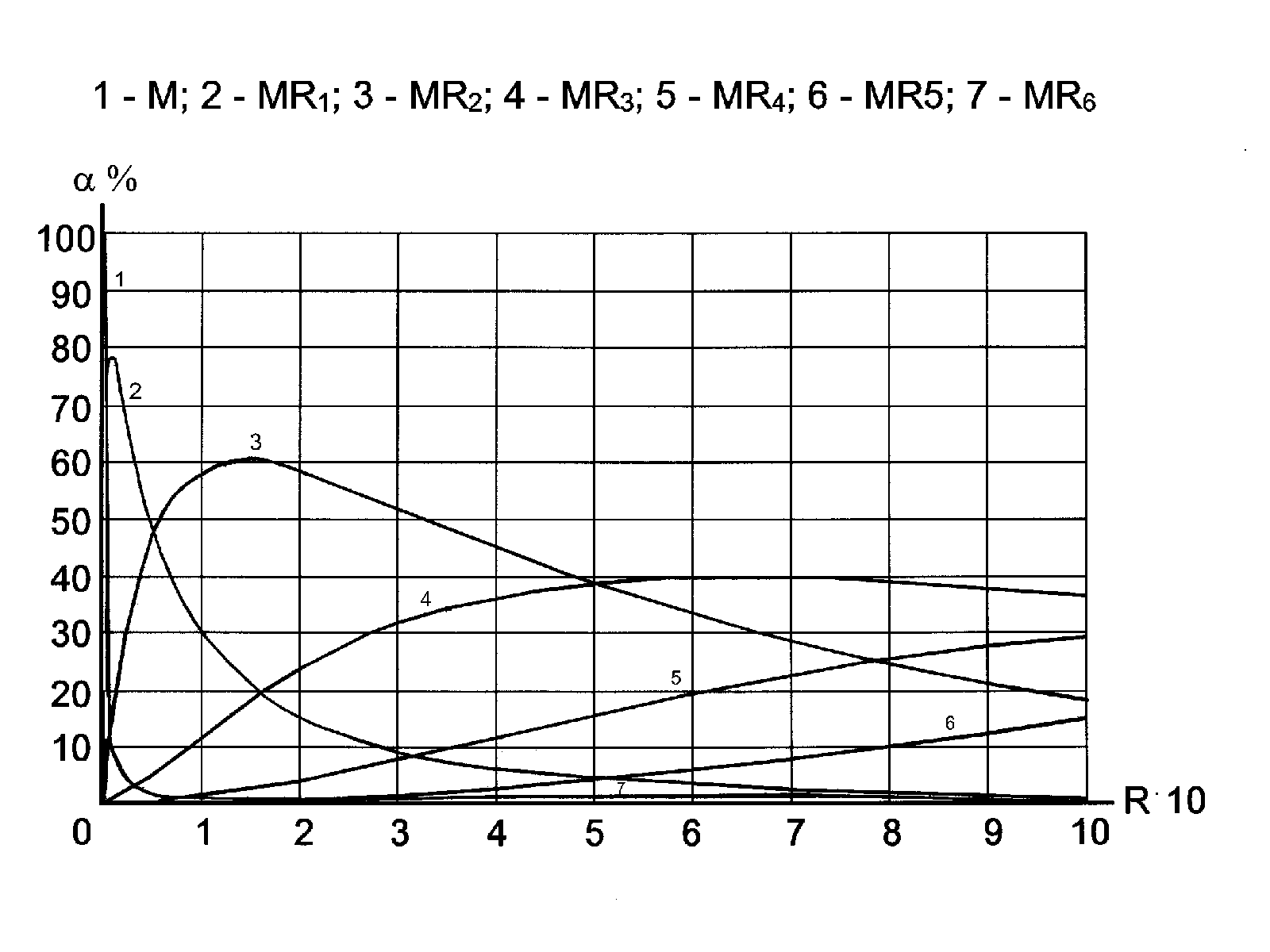



₁ = 10^1,03 / 13,9 = 0,77, т.е. выход монороданидного комплекса составляет 77% от общей концентрации железа(III) в растворе (рис.2).

Рис.2. Диаграмма распределения железороданидных комплексов

3. Вычислить, какую концентрацию аммиака (избыточную) надо создать в растворе при С_Аg = 10^-4 моль/л, чтобы снизить концентрацию катионов Ag⁺ в 1000 раз.

Решение. Очевидно, надо добиться закомплексованности серебра Ф = 1000. При избытке аммиака в растворе доминирует насыщенный комплекс Ag(NH₃)₂⁺. Пренебрегаем существованием ненасыщенного комплекса AgNH₃⁺ и рассчитываем концентрацию свободного лиганда по приближенной формуле (23), концентрация серебра при этом не важна:

[ NH₃ ]    10 ^-2,1  8·10^-3 (моль/л).

4. Какую концентрацию молекул аммиака надо создать в растворе, чтобы при рН 8 медь (II) оставалась в растворе в виде аммиачного комплекса и не выпадала в осадок в виде гидроксида? Начальная концентрация меди(II) равна 10^-4 моль/литр.

Решение. Рассчитаем, при какой концентрации свободных ионов меди при рН 6 начнется осаждение Cu(OH)₂. Величина ПР_Сu(OH)2 10^-32, откуда

[Cu] = = = 10^-16.

Чтобы осадок гидроксида меди не выпадал при рН 7, надо понизить концентрацию свободных ионов меди с 10^-4 до 10^-16, т.е. добиться закомплексованности, равной 10¹² (можно и больше!). Концентрацию аммиака, создающую такую закомплексованность, рассчитаем по формуле (23), учитывая образование комплекса состава 1:4 и пренебрегая возможным образованием ненасыщенных аммиакатов меди:

[NH₃]    1 (моль/л).
5. Кадмий (II) образует в растворе с иодид-ионами комплексные соединения различного состава, от 1:1 до 1:4. Какой именно комплекс доминирует при [I^-]=0,1 моль/л?

Решение. Выше указывалось, что при одновременном существовании нескольких комплексов выход каждого из них пропорционален величине 10 ^{lgi -ipL}. Следовательно, доминировать будет комплекс, у которого при данной концентрации лиганда этот показатель окажется наибольшим. Для системы Сd²⁺ - I^- выпишем общие константы устойчивости всех иодидных комплексов и рассчитаем для этих комплексов разности (lg_i -ipL). В данном случае [L] = 0,1 моль/л, следовательно, рL=1. Хотя рассчитанные значения разностей не слишком сильно отличаются между собой (см. таблицу): расчет степени образования каждого комплекса по формуле (24) показывает, что в данных условиях доминирует насыщенный комплекс СdI₄^2-

Комплекс	lg 	lg i - i pL	, %
СdI+	2,28	2,28 - 1 = 1,28	5,8
CdI2	3,92	3,92 - 2 = 1,92	25,3
CdI3-	6,10	5,00 - 3 = 2,00	30,5
CdI42-	5,00	6,10 - 4 = 2,10	38,4

При малом же избытке лиганда могут доминировать и ненасыщенные комплексы. Так, в той же системе при [I^-]=0,010 доминирует комплекс состава 1:1, т.е. CdI⁺.

Контрольные вопросы

1. Какие соединения называют комплексными? Kакой тип связи в них реализуется?

2. Дайте определения понятиям координационное число, центральный атом, лиганд, дентатность, хелаты, хелатоэффект.

3. Какие элементы обычно выступают в роли центральных атомов, какие из них дают (при прочих равных условиях) наиболее прочные комплексы?

4. Какие частицы в растворе могут участвовать в реакциях комплексообразования в качестве лигандов? Дайте примеры моно-, би-, три- и полидентатных лигандов.

5. Какие особенности в своем строении имеют органические молекулы, способные быть полидентатными лигандами?

6. По одной из классификаций все комплексы делят на устойчивые и нестойкие, по другой - на стабильные и лабильные. Какой признак положен в основу этих классификаций?

7. Для каких именно целей применяют комплексные соединения в химическом анализе?

8. Что такое закомплексованность? Как определить ее опытным путем и подсчитать без специальных экспериментов?

9. Напишите схему ступенчатого комплексообразования в системе Cd²⁺ - I^, выпишите формулы для расчета общих и ступенчатых констант устойчивости комплексов кадмия.

10. Как получить значения ступенчатых констант устойчивости, если в справочнике имеются только данные по общим константам?

11. Как подсчитать степень образования некоторого комплекса, если идет процесс ступенчатого комплексообразования? Как меняется состав смеси комплексов при изменении концентрационных условий?

12. Как вычислить концентрацию лиганда, необходимую для заданной степени закомплексованности металла? Для максимального выхода комплекса ML_i ?