Эконометрика-Практикум-Елисеева. Практикум по эконометрике под редакцией членакорреспондента Российской Академии наук И. И. Елисеевой

• Название: Практикум по эконометрике под редакцией членакорреспондента Российской Академии наук И. И. Елисеевой
• Дата: 17.06.2022
• Размер: 4.16 Mb.
• Имя файла: Эконометрика-Практикум-Елисеева.doc
• Тип: Практикум; #599190
• страница: 18 из 26

РАЗДЕЛ IV. ВРЕМЕННЫЕ РЯДЫ В ЭКОНОМЕТРИЧЕСКИХ ИССЛЕДОВАНИЯХ

4.1. МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Модели, построенные по данным, характеризующим один объект за ряд последовательных моментов (периодов), называются моделями временных рядов.

Временной ряд - это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов.

Каждый уровень временного ряда формируется из трендовой (Т), циклической (S) и случайной (Е) компонент.

Модели, в которых временной ряд представлен как сумма перечисленных компонент, - аддитивные модели, как произведение -мультипликативные модели временного ряда.

Аддитивная модель имеет вид: Y = Т + S + Е;

мультипликативная модель: Y=T • S • Е.

Построение аддитивной и мультипликативной моделей сводится к расчету значений T, S и Е для каждого уровня ряда.

Построение модели включает следующие шаги;

1) выравнивание исходного ряда методом скользящей средней;

2) расчет значений сезонной компоненты S;

3) устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных в аддитивной (T + Е) или в мультипликативной (T • Е) модели;

4) аналитическое выравнивание уровней (T + Е) или (Т • Е) и расчет значений Т с использованием полученного уравнения тренда;

5) расчет полученных по модели значений (Y+ S) или (Т • S);

6) расчет абсолютных и/или относительных ошибок.

Автокорреляция уровней ряда - это корреляционная зависимость между последовательными уровнями временного ряда: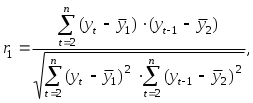



где 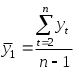; 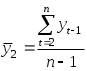- коэффициент автокорреляции уровней ряда первого порядка;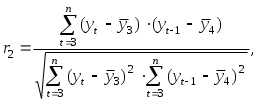



где 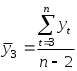; 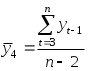^- коэффициент автокорреляции уровней ряда второго порядка.

Формулы для расчета коэффициентов автокорреляции старших порядков легко получить из формулы линейного коэффициента корреляции.

Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называют автокорреляционной функцией временного ряда, а график зависимости ее значений от величины лага (порядка коэффициента автокорреляции) - коррелограммой.

Построение аналитической функции для моделирования тенденции (тренда) временного ряда называют аналитическим выравниванием временного ряда. Для этого чаще всего применяются следующие функции:

• линейная = а + b • t;

• гипербола = а + b/t ;

• экспонента = e^a+bt,

• степенная функция = а•t^b,

• парабола второго и более высоких порядков

= а + b₁ • t + b₂ • t² + ... + b_k • t^k.

Параметры трендов определяются обычным МНК, в качестве независимой переменной выступает время t = 1, 2, ..., п, а в качестве зависимой переменной - фактические уровни временного ряда у_t. Критерием отбора наилучшей формы тренда является наибольшее значение скорректированного коэффициента детерминации .

При построении моделей регрессии по временным рядам для устранения тенденции используются следующие методы.

Метод отклонений от тренда предполагает вычисление трендовых значений для каждого временного ряда модели, например и , и расчет отклонений от трендов: и . Для дальнейшего анализа используют не исходные данные, а отклонения от тренда.

Метод последовательных разностей заключается в следующем:

если ряд содержит линейный тренд, тогда исходные данные заменяются первыми разностями:

;

если параболический тренд - вторыми разностями:

.

В случае экспоненциального и степенного тренда метод последовательных разностей применяется к логарифмам исходных данных.

Модель, включающая фактор времени, имеет вид

.

Параметры а и b этой модели определяются обычным МНК.

Автокорреляция в остатках - корреляционная зависимость между значениями остатков е, за текущий и предыдущие моменты времени.

Для определения автокорреляции остатков используют критерий Дарбина - Уотсона и расчет величины: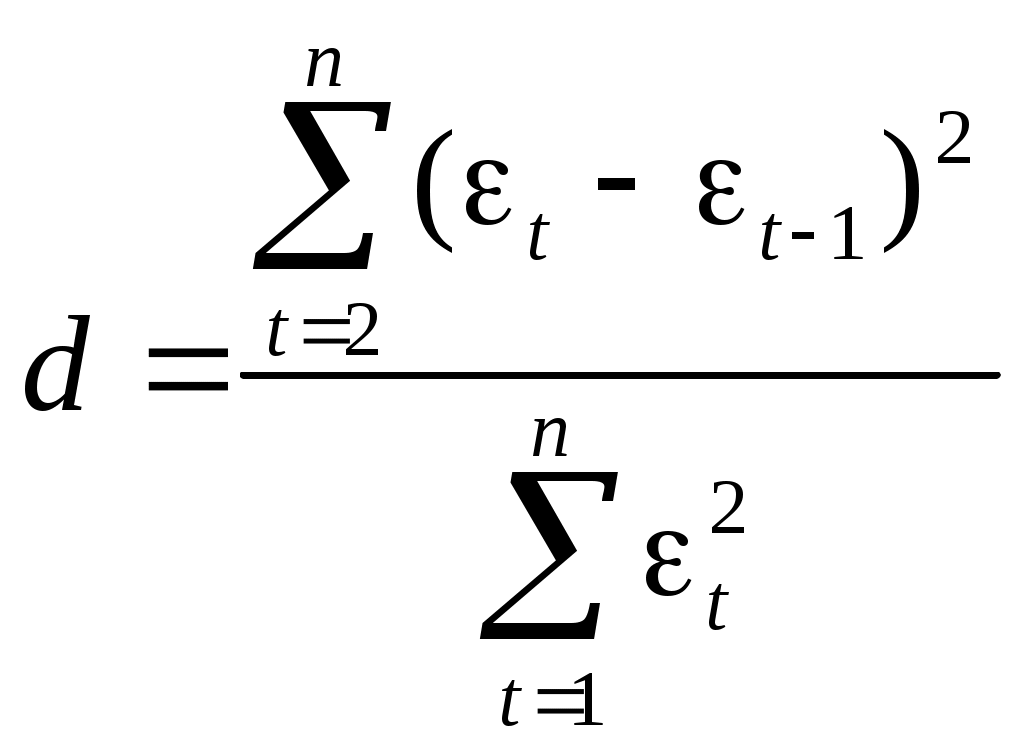

, 0  d 4.

Коэффициент автокорреляции остатков первого порядка определяется по формуле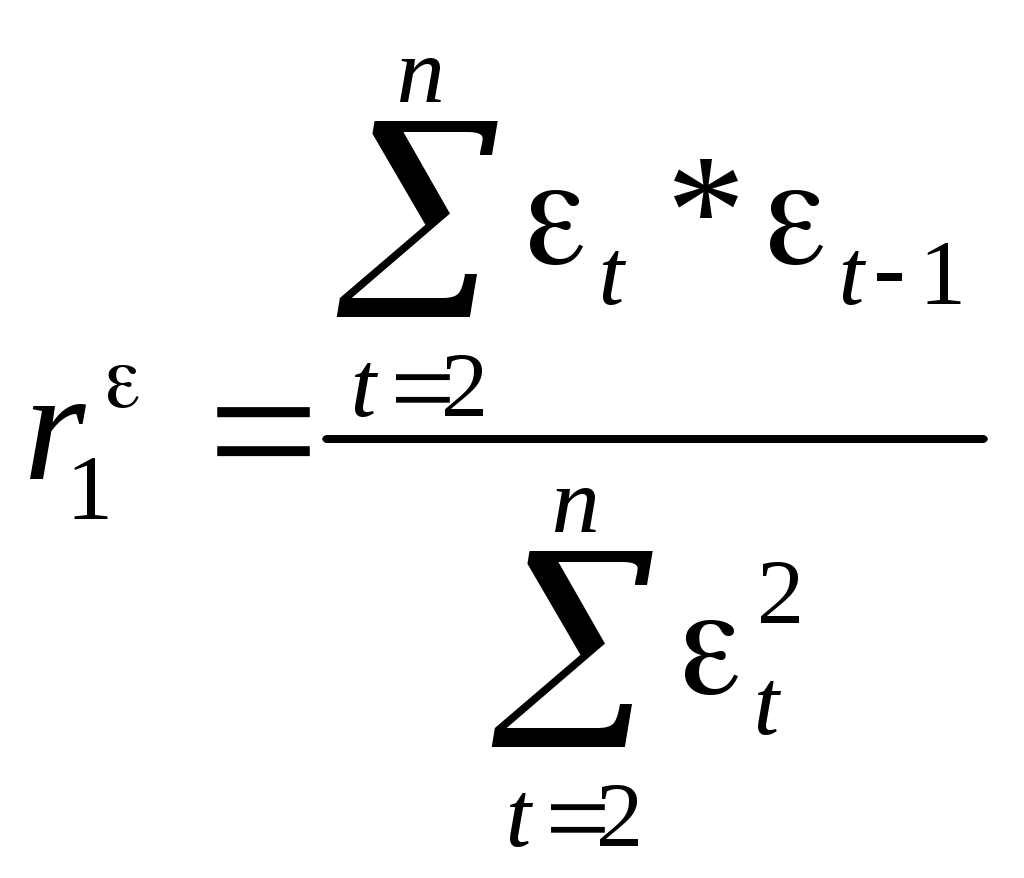

, .

Критерий Дарбина - Уотсона и коэффициент автокорреляции остатков первого порядка связаны соотношением

.

Эконометрические модели, содержащие не только текущие, но и лаговые значения факторных переменных, называются моделями с распределенным лагом.

Модель с распределенным лагом в предположении, что максимальная величина лага конечна, имеет вид

.

Коэффициент регрессии b₀ при переменной х_t характеризует среднее абсолютное изменение у_t при изменении х_t на 1 ед. своего измерения в некоторый фиксированный момент времени t, без учета воздействия лаговых значений фактора х. Этот коэффициент называют краткосрочным мультипликатором.

В момент (t + 1) воздействие факторной переменной х_t на результат у_t составит (b₀ + b₁) условных единиц; в момент времени (t + 2) воздействие можно охарактеризовать суммой (b₀ + b₁ + b₂) и т.д. Эти суммы называют промежуточными мультипликаторами. Для максимального лага (t + l) воздействие фактора на результат описывается суммой (b₀ + b₁ + ... + b_l = b), которая называется долгосрочным мультипликатором.

Величины

, ,

называются относительными коэффициентами модели с распределенным лагом. Если все коэффициенты b_j имеют одинаковые знаки, то для любого j

и .

Величина среднего лага модели множественной регрессии определяется по формуле средней арифметической взвешенной:



и представляет собой средний период, в течение которого будет происходить изменение результата под воздействием изменения фактора в момент t.

Медианный лаг - это период, в течение которого с момента времени t будет реализована половина общего воздействия фактора на результат:

,

где l_Me - медианный лаг.

Оценку параметров моделей с распределенными лагами можно проводить согласно одному из двух методов: методу Койка или методу Алмон.

В распределении Койка делается предположение, что коэффициенты при лаговых значениях объясняющей переменной убывают в геометрической прогрессии:

b_l = b₀*^l, l= 0,1,2,..., 0<<1.

Уравнение регрессии преобразуется к виду

.

После несложных преобразований получаем уравнение, оценки параметров которого приводят к оценкам параметров исходного уравнения.

В методе Алмон предполагается, что веса текущих и лаговых значений объясняющих переменных подчиняются полиномиальному распределению:

.

Уравнение регрессии примет вид

,

где , i= l, ...,k;j = 1,...,p.

Расчет параметров модели с распределенным лагом методом Алмон проводится по следующей схеме:

1) устанавливается максимальная величина лага l;

2) определяется степень полинома k, описывающего структуру лага;

3) рассчитываются значения переменных z₀, ..., z_k;

4) определяются параметры уравнения линейной регрессии y_t от z_i;

5) рассчитываются параметры исходной модели с распределенным лагом.

Модели, содержащие в качестве факторов лаговые значения зависимой переменной, называются моделями авторегрессии, например:

.

Как и в модели с распределенным лагом, b₀ в этой модели характеризует краткосрочное изменение y_t под воздействием изменения x_tна 1 ед. Долгосрочный мультипликатор в модели авторегрессии рассчитывается как сумма краткосрочного и промежуточных мультипликаторов:

.

Отметим, что такая интерпретация коэффициентов модели авторегрессии и расчет долгосрочного мультипликатора основаны на предпосылке о наличии бесконечного лага в воздействии текущего значения зависимой переменной на ее будущие значения.