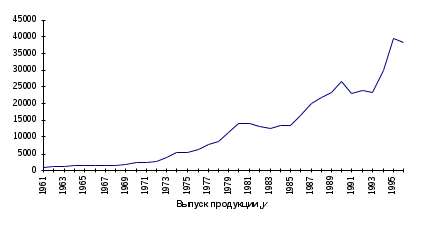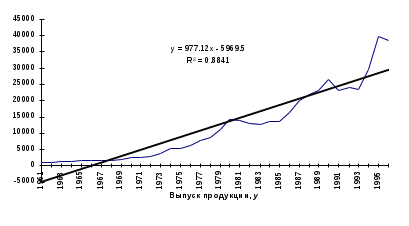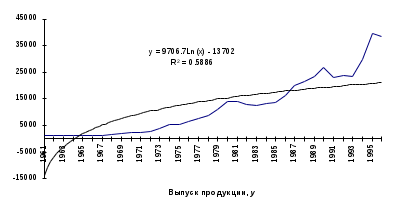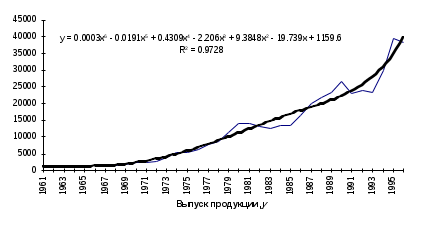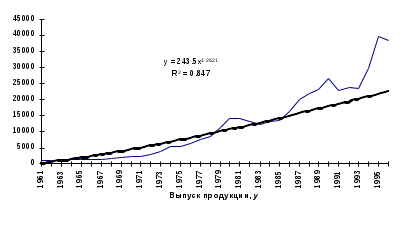Эконометрика-Практикум-Елисеева. Практикум по эконометрике под редакцией членакорреспондента Российской Академии наук И. И. Елисеевой

• Название: Практикум по эконометрике под редакцией членакорреспондента Российской Академии наук И. И. Елисеевой
• Дата: 17.06.2022
• Размер: 4.16 Mb.
• Имя файла: Эконометрика-Практикум-Елисеева.doc
• Тип: Практикум; #599190
• страница: 20 из 26

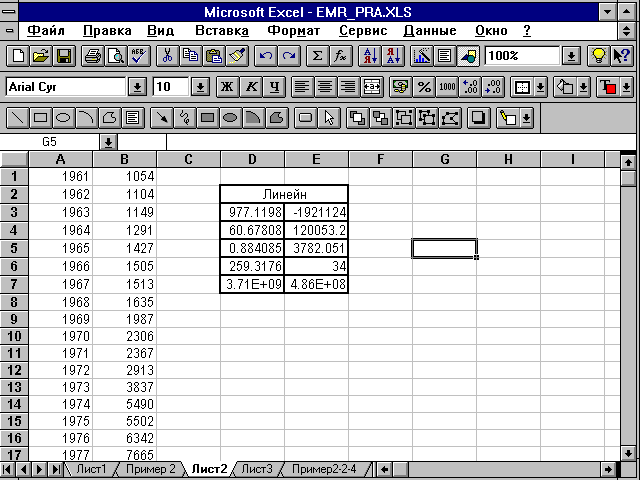
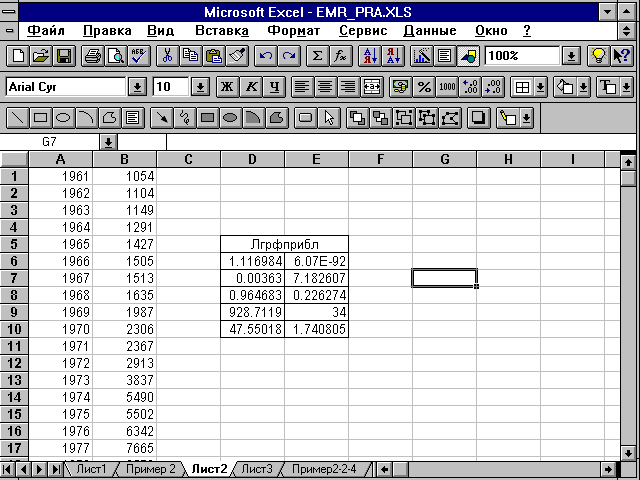
4.3. РЕАЛИЗАЦИЯ ТИПОВЫХ ЗАДАЧ НА КОМПЬЮТЕРЕ

Решение с использованием ППП MSExcel

1. Для определения параметров линейного тренда по методу наименьших квадратов используется статистическая функция ЛИНЕЙН, для определения экспоненциального тренда - ЛГРФПРИБЛ. Порядок вычисления был рассмотрен в 1-м разделе практикума. В качестве зависимой переменной в данном примере выступает время (t = 1, 2, ..., n). Приведем результаты вычисления функций ЛИНЕЙН и ЛГРФПРИБЛ (рис. 4.2 и 4.3).

Рис. 4.2. Результат вычисления функции ЛИНЕЙН

Рис. 4.3. Результат вычисления функции ЛГРФПРИБЛ

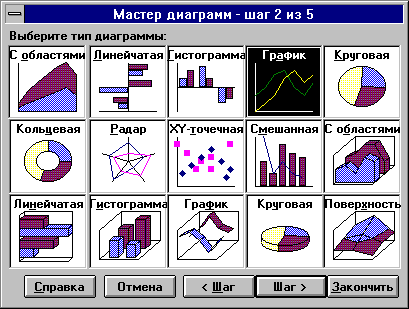
Запишем уравнения линейного и экспоненциального тренда используя данные рис. 4.2 и 4.3:

,

.

2. Построение графиков осуществляется с помощью Мастера диаграмм. '

Порядок построения следующий:

1) введите исходные данные или откройте существующий файл содержащий анализируемые данные;

2) активизируйте Мастер диаграмм любым из следующих способов:

а) в главном меню выберите Вставка/Диаграмма;

б) на панели инструментов Стандартная щелкните по кнопке Мастер диаграмм;

3) в окне Тип выберите График (рис. 4.4); вид графика выберите в поле рядом со списком типов. Щелкните по кнопке Далее;

Рис. 4.4. Диалоговое окно Мастера диаграмм: тип диаграммы

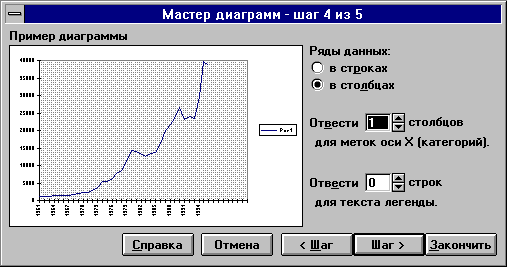
4) заполните диапазон данных, как показано на рис. 4.5. Установите флажок размещения данных в столбцах (строках). Щелкните по кнопке Далее;

Рис. 4.5. Диалоговое окно Мастера диаграмм: источник данных

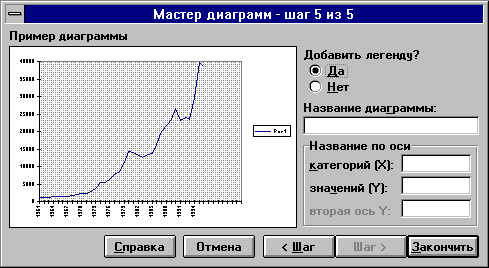
5) заполните параметры диаграммы на разных закладках (рис. 4.6): названия диаграммы и осей, значения осей, линии сетки, параметры легенды, таблица и подписи данных. Щелкните по кнопке Далее;

Рис. 4.6. Диалоговое окно Мастера диаграмм: параметры диаграммы

6) укажите место размещения диаграммы на отдельном или на имеющемся листе (рис. 4.7). Щелкните по кнопке Далее. Готовая диаграмма, отражающая динамику уровней изучаемого ряда, представлена на рис. 4.8.

XXXXX

Рис. 4.7. Диалоговое окно Мастера диаграмм: размещение диаграммы

Рис. 4.8. Динамика выпуска продукции

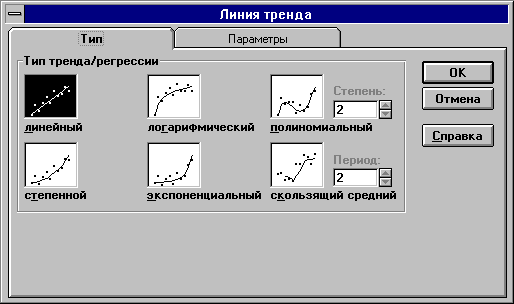
В ППП MS Excel линия тренда может быть добавлена в диаграмму с областями гистограммы или в график. Для этого:

1) выделите область построения диаграммы; в главном меню выберите Диаграмма/Добавить линию тренда;

2) в появившемся диалоговом окне (рис. 4.9) выберите вид линии тренда и задайте соответствующие параметры. Для полиномиального тренда необходимо задать степень аппроксимирующего полинома, для скользящего среднего - количество точек усреднения.

Рис. 4.9. Диалоговое окно типов линий тренда

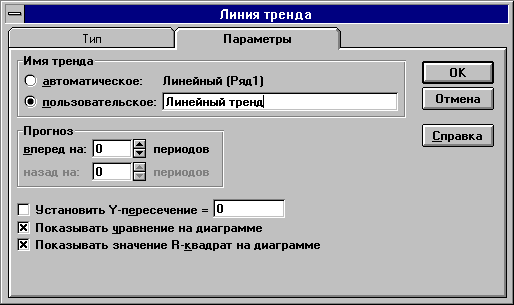
В качестве дополнительной информации на диаграмме можно отобразить уравнение регрессии и значение среднеквадратического отклонения, установив соответствующие флажки на закладке Параметры (рис. 4.10). Щелкните по кнопке ОК.

Рис. 4.10. Диалоговое окно параметров линии тренда

На рис. 4.11 - 4.15 представлены различные виды трендов, описывающие исходные данные задачи.

Рис. 4.11. Линейный тренд

Рис. 4.12. Логарифмический тренд

Рис. 4.13. Полиномиальный тренд

Рис. 4.14. Степенной тренд

Рис. 4.15. Экспоненциальный тренд

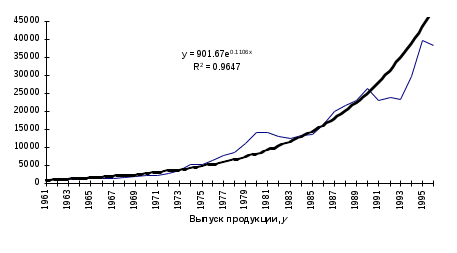
3. Сравним значения R² по разным уравнениям трендов:

- полиномиальный 6-й степени - R² = 0 9728;

- экспоненциальный - R² = 0,9647;

- линейный - R² = 0,8841;

степенной - R² = 0,8470;

логарифмический - R² = 0,5886.

Исходные данные лучше всего описывает полином 6-й степени. Следовательно, в рассматриваемом примере для расчета прогнозных значении следует использовать полиномиальное уравнение.

Пример 6

Имеются данные о динамике товарооборота и доходов населения России за 1997 - 1999 гг. (табл. 4.8).

Таблица 4.8

Месяц	Товарооборот, % к предыдущему месяцу	Доходы населения, % к предыдущему месяцу
Январь	91.5	79.5
Февраль	92.8	100.3
Март	104.3	102.9
Апрель	101.5	106.6
Май	97.9	92.5
Июнь	98.7	110.1
Июль	100.8	96.6
Август	103.7	97.1
Сентябрь	104.6	98.5
Октябрь	100.3	105.7
Ноябрь	101.5	97.4
Декабрь	116.0	129.9
Январь	82.3	63.9
Февраль	91.6	104.3
Март	103.4	101.7
Апрель	100.3	105.5
Май	99.2	91.3
Июнь	99.0	102.6
Июль	102.3	102.6
Август	106.8	96.6
Сентябрь	96.7	81.5
Октябрь	92.7	107.8
Ноябрь	100.4	69.7
Декабрь	108.1	122.8
Январь	80.0	63.9
Февраль	96.9	107.4
Март	106.0	103.7
Апрель	97.6	108.1
Май	100.2	93.9
Июнь	100.7	104.1
Июль	100.0	97.2
Август	106.5	104.6
Сентябрь	100.5	98.6
Октябрь	102.1	104.5
Ноябрь	100.5	99.9
Декабрь	116.0	136.9

Требуется:

1. Оценить параметры модели с распределенными лагами методом Алмон.

2. Постройте таблицу результатов дисперсионного анализа. Оцените значимость построенной модели.

Решение

Решение с использованием ППП Statistica

1. Для построения регрессионной модели с распределенными лагами необходимо априори задать длину максимального лага, для этой задачи выберем длину 3. Тогда уравнение регрессии будет выглядеть следующим образом:



Для оценки параметров этой модели согласно методу Алмон необходимо задать степень аппроксимирующего полинома. Для решения используем соответствующую процедуру ППП Statistica. Порядок расчетов следующий:

1) введите исходные данные или откройте существующий файл другого формата, содержащий анализируемые данные, в опции Data Management в окне переключения модулей (рис. 4.16). Если создаете новый файл данных, в соответствующих ячейках укажите количество строк и столбцов. В нашем случае - 2 столбца, 36 строк;

XXXXX

Рис. 4.16. Окно переключения модулей

2) из модуля управления данными перейдите в модуль анализа временных рядов, выбрав в меню пункт Time Series / Forecasting;

XXXXX

Рис. 4.17. Окно анализа временных рядов

3) откройте файл, содержащий данные - Open Data (рис. 4.17);

4) выделите все переменные, используемые для анализа, - Variables. Щелкните по кнопке ОК (рис. 4.18).

XXXXX

Рис. 4.18. Выбор переменных для анализа

5) щелкните по кнопке Distributed lags analysis (см. рис, 4.17);

XXXXX

Рис. 4.19. Окно анализа моделей с распределенными лагами

6) в окне Distributed Lags Analysis (рис. 4.19) выделите название зависимой переменной, в появляющемся окне Independent variable -название независимой переменной. В ячейке Lag length укажите значение максимального лага, в ячейке Almon polynomial lags - степень аппроксимирующего полинома. Степень полинома не должна превышать значение максимального лага. Щелкните по кнопке ОК (Begin analysis);

7) результаты расчетов - оценки регрессионных коэффициентов и значимость уравнения - приведены на рис. 4.20 и 4.21.

XXXXX

Рис. 4.20. Оценки параметров уравнения с распределенным лагом

XXXXX

Рис. 4.21. Результаты дисперсионного анализа

2. Согласно данным таблицы дисперсионного анализа (см. рис. 4.21), полученные значения F-критерия Фишера и коэффициента детерминации R² показывают высокий уровень аппроксимации исходных данных.