Прогнозирование Парсаданов. Программа Культура России
 Скачать 2.29 Mb. Скачать 2.29 Mb.
|
|
Оценка метода «семи матриц». Основные преимущества рассмотренного метода сводятся к следующим. Он позволяет на практике реализовать принципы системности и развития в научном предвидении, объединяя анализ взаимодействия природных, научно-технических, экономических и социально-политических факторов общим стержнем единого сценария. Таким образом, развитие производительных сил, производственных отношений обусловливается как внутренними противоречиями, так и причинными воздействиями, передаваемыми другими подсистемами. В процессе подготовки, реализации и анализа результатов прогноза в поле зрения постоянно находятся не только экономические, но и природно-технические, а также социально-политические факторы, которые зачастую скрыты от экономиста узостью его знаний в смежных областях. На первый план выступает необходимость тщательного формулирования гипотез, закладываемых в основу сценария, проверки их совместимости. Обратная связь, предусмотренная в схеме анализа, требует постоянного сопоставления исходных гипотез и результатов прогнозных экспериментов. Последнее позволяет упрочить аргументацию относительно вероятности осуществления определенного варианта в действительности и вносит целенаправленность в процесс корректировки прогнозных сценариев. Качественная реализация предложенной схемы возможна лишь при плодотворном сотрудничестве специалистов различных отраслей науки: экономистов-страновиков, экономистов-международников, историков, социологов, психологов, экологов, специалистов в области международных отношений. Подобное сотрудничество привносит мощные импульсы развитию теоретической мысли, которые исходят от смежных дисциплин. Задача экономиста-математика сводится к получению (при заданных сценариях) данных о динамике экономических индикаторов. Последующий анализ — дело специалистов смежных отраслей науки. Макроэкономические переменные, получаемые на выходе модели, можно рассматривать как индикаторы, характеризующие состояние социально-экономической системы. Каждый из них характеризует развитие того или иного противоречия и является, по сути дела, синтетическим интегральным индикатором. Его динамику определяет целая гамма факторов, которые можно рассматривать как частные индикаторы. Первостепенное значение имеет анализ экономических и социально-политических последствий попадания значения индикаторав «опасную зону», т.е. переход значения индикатора через «пороговую» величину. Однако следует отметить, что построение всех матриц — долгий и кропотливый процесс, требующий много времени и внимания. Но так как в работе над сценарием участвует большой отряд специалистов различного направления, степень совпадения исходных предпосылок и конечных результатов достаточно велика, и возможность действительной реализации данного сценария весьма существенна. Метод исторических аналогий Метод исторических аналогий эффективен при определении путей развития новых отраслей и экономических районов. Но и принятый «образец» нуждается в дальнейшем исследовании внутренних и внешних условий его развития и закономерностей этого развития. Необходимо очень осторожно применять этот метод, так как нет абсолютно одинаковых объектов и явлений, и к тому же изменяется как внутренняя, так и внешняя среда объекта. Особенно важно корректное использование этого метода при прогнозировании развития социально-экономической системы страны. Например, очень сомнительна возможность использования для прогнозирования выхода из кризиса и стабилизации социально-экономической системы России моделей, использованных Польшей, Венгрией, Китаем, Чили, Аргентиной. Например, Польша отличается от России компактной территорией, однородностью населения, одной религией, объединяющей народ, наличием частной собственности в сельском хозяйстве, существовавшей даже в рамках административно-командной системы. Прогнозируя развитие России, необходимо учитывать как изменившиеся внутренние условия за последние годы, так и внешние условия (например, связанные с мировым финансовым кризисом). В урезанном виде метод аналогии может быть использован и в комплексных методах, например, для прогнозирования изменений в параметрах математических моделей. Такие аналогии обычно называют математическими, так как в данном случае объект прогнозирования или его часть описывается при помощи математического аппарата, который разрабатывался в интересах другого объекта, но выявленные закономерности в описании его развития позволили его использовать в интересах исследуемого объекта. 3.3.2. Математические модели прогнозирования Метод экстраполяции тренда Трендовая модель — это математическая модель, описывающая изменение прогнозируемого или анализируемого показателя только в зависимости от времени и имеющая вид: у = f(t). Она описывает тенденцию развития (изменения) достаточно стабильной социально-экономической системы во времени, в особенности таких агрегированных показателей развития, как ВНП (ВВП), ЧНП, НД, уровень инфляции, безработицы Метод, использующий трендовые модели в прогнозировании, называется методом экстраполяции тренда. Это один из пассивных методов прогнозирования и называется «наивным» прогнозом, так как предполагает строгую инерционность развития, которая представляется в виде проектирования прошлых тенденций в будущее, а главное — независимость показателей развития от тех или иных факторов. Ясно, что нельзя переносить тенденции, которые сформировались в прошлом, на будущее. Причины этого следующие: а) при краткосрочном прогнозировании экстраполяция прошлых усредненных показателей приводит к тому, что пренебрегаются (или остаются незамеченными) необычные отклонения в обе стороны от тенденций. В то же время для текущего (краткосрочного) прогноза или плана основной задачей является предвидение этих отклонений; б) при долгосрочном прогнозировании используется такой высокий уровень агрегирования, при котором не учитываются изменения структуры производимой продукции, самой продукции, изменение технологии производства, особенностей рынков, т.е. все то, что составляет главные задачи стратегического планирования. Социально-экономическая система в отличие от замкнутой физической системы — открытая и реагирующая система, изменяющаяся в зависимости от внешних условий и ввода новых переменных. Поэтому если анализ ситуаций на основе ретроспективного взгляда может быть более или менее успешным, то прогнозирование будущего, как правило, оказывается неудачным. Важно то, что детальный и внимательный анализ хода развития в прошлом почти всегда выявляет спады деловой активности, которые прекращаются и ликвидируются не пассивным ожиданием «естественных сил», восстанавливающих равновесие, а энергичными управленческими усилиями государственных органов, направленными на преодоление неблагоприятных обстоятельств. Статистический анализ, проводимый с целью экстраполяции, зачастую нацелен на выявление характера противодействия со стороны управленческого аппарата, предотвращающего ожидаемые спады. Необходимо, чтобы при анализе ставилась и решалась задача выявления характера государственного регулирования, государственной экономической политики, эффективности различных мероприятий в различных условиях. Не надо пренебрегать скачкообразными колебаниями при ретроспективном анализе. Необходимо проводить анализ не только по агрегированной номенклатуре товаров, иначе можно «упустить» начало структурных сдвигов. Резюмируя вышеназванное, можно отметить, что необходимо очень осторожно переносить тенденции, которые сформировались в прошлом, на будущее по следующим причинам: а) в будущем может измениться эффективность многих факторов, в том числе темпы использования достижений НТП; б) прошлое определялось не только «естественным» развитием экономических процессов, а в достаточно большой мере государственной политикой в управлении экономикой, методами государственного регулирования; в) экстраполяция из-за высокой агрегированное™ макроэкономических показателей не выявляет изменений структуры производства, структурных сдвигов в развитии отраслей, регионов. Многие авторы предостерегают от излишнего увлечения экстраполяцией тренда социально-экономических показателей, так как даже на микроуровне тренд считается лишь отправной базой для прогнозирования, инструментом получения «прогностического сырья». Экстраполяция тренда используется в основном в оперативном прогнозировании, а в стабильных СЭС — ив краткосрочном. Метод эконометрического моделирования Одним из важнейших инструментов анализа и прогноза социально-экономических систем является метод эконометрического моделирования, который наиболее эффективен в случае систем с устойчивыми, стабильными тенденциями развития. Рассмотрим различные модификации эконометрической модели (ЭКМ). ЭКМ может состоять из одного уравнения регрессии (стохастического уравнения) с одним фактором. Например: у = а0 + а1x1— линейное уравнение, где а0— свободный член, а1— коэффициент регрессии. Классический пример — кейнсианская модель: Сn = f (D0), или Сn= а0 +axD0 , где Сn— потребительский спрос, D0 — личный располагаемый доход прогнозируемого года. ЭКМ может состоять из одного регрессионного уравнения с несколькими факторами, т. е. многофакторного уравнения. Например: у = а0 + a1xl+a2x2+...+anxn, где п — число факторов. ЭКМ может состоять из нескольких регрессионных уравнений. Эти уравнения называются одновременными, так как решаются как бы в одно и то же время последовательно друг за другом. При этом они могут быть взаимоувязаны, т.е. результирующие переменные первого уравнения используются как факторы для нахождения результирующей переменной второго уравнения. Уравнения регрессии могут быть и независимы друг от друга. При этом каждое уравнение решается самостоятельно, независимо от других уравнений. Система линейных взаимоувязанных уравнений выглядит так: 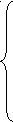 x1 = a0 + a2x2 x3 = b0 + b1x1 x4 = y0 + y1x1 + y2x2. В этой эконометрической модели х1, x2и х4 — эндогенные переменные, моделируемые в рамках данной ЭКМ, а x2— экзогенный показатель, прогнозируемый вне данной ЭКМ (в рамках другой модели или экспертным путем). Классическим примером ЭКМ, состоящей из независимых уравнений, является модель равновесия совокупного спроса и совокупного предложения. В ЭКМ могут использоваться и трендовые модели, например, один или несколько экзогенных показателей, изменения которых во времени носит «плавный» характер, могут быть спрогнозированы по трендовой модели y = f(t). Хотя можно считать, что это — внемодельное прогнозирование, так как прогнозируется экзогенный фактор. В рамках расчетов по ЭКМ для прогнозирования экзогенных переменных используются также методы экспертных оценок. В ЭКМ могут быть использованы и авторегрессионные уравнения типа у, = f (yt-1, yt-2, …, yt-m),в которых значение результирующего показателя (у) в любое время (t) является функцией значений этого же показателя за ряд предыдущих лет. Наряду с регрессионными уравнениями, описывающими вероятностные (стохастические) процессы, в ЭКМ включаются и так называемые дефинщионные уравнения, или тождества. Например, в модели прогнозируются государственные (Jg) и частные (Jp) инвестиции двумя независимыми регрессионными уравнениями, а третье уравнение позволяет рассчитать прогнозное значение общих инвестиций: J = Jg+Jp— это тождество. В ЭКМ используются и так называемые «уравнения равновесия», по форме похожие на тождества. Например, уравнение, выражающее условие равновесия на товарном рынке: AD = AS— совокупный спрос равен совокупному предложению. В общем случае ЭКМ называют системой регрессионных уравнений и тождеств. Некоторые авторы называют регрессионные уравнения «объясняющими» уравнениями, так как изменение значений совокупности факторов-аргументов объясняют изменение результирующей переменной, вернее, часть общего реального изменения. Чем больше объясняемая часть, тем лучше (адекватнее) регрессионное уравнение объясняет реальность. Тогда напрашивается вопрос, какая разница между методом экстраполяции тренда и эконометрическим методом? Дело в том, что если выявленные зависимости между функцией (У) и факторами-аргументами (X) используются без изменения, т. е. экстраполируются, разница только в том, что эконометрический метод позволяет провести содержательный анализ зависимости исследуемого (прогнозируемого) показателя от того или иного показателя, а экстраполяция тренда отражает только изменение изучаемого показателя во времени. Но основное отличие заключается в том, что эконометрические модели позволяют разрабатывать варианты развития социально-экономического объекта путем изменений условий его функционирования (активное прогнозирование), приводящих к различным значениям эндогенных факторов, изменению трендов их соотношений путем варьирования значений экзогенных факторов, также отличных от тенденций их изменения во времени. Как правило, варианты развития отличаются различными значениями экзогенных факторов, так как они не моделируются в рамках ЭКМ, они неуправляемы, и интервал их возможных значений в будущем определяется методом экспертных оценок. Варианты могут отличаться и различными значениями инструментов государственного регулирования, количеством и уровнем налогов, учетной ставкой, нормой обязательных резервов. Рассмотрев сущность и содержание ЭКМ, перейдем к конкретному описанию порядка (алгоритма) разработки ЭКМ, используя опыт моделирования Японии1. 1. Прежде чем приступить к процессу разработки ЭКМ, ставится цель (цели), ради достижения которой разрабатывается ЭКМ. Например, при разработке долгосрочной модели Японии на 20-летний период прогнозирования ставилась такая общая для всех моделей этого типа цель, как выявление перспектив роста производства СЭС в физическом выражении (в неизменных ценах) на основе данных, содержащихся в счетах национального дохода. В то же время ставилась и конкретная цель — исследовать тенденцию таких компонентов основных фондов, как государственные и частные инвестиции в жилищное строительство и установить их связь с общим ростом экономики. Акцент на эти компоненты основных фондов продиктован тем, что для Японии они являются наиболее существенными факторами, определяющими долговременное развитие СЭС, и тем обстоятельством, что вторая цель может быть достигнута только в долгосрочном периоде из-за длительности формирования и сроков службы этих компонентов. Цели модели Японии на 10-летний период прогнозирования в основном совпадают с целями модели 20-летнего периода, но первая преследует и другие специфические цели, а именно:
Если долгосрочные модели позволяют представить пути развития СЭС на уровне высокоагрегированных макропоказателей, то среднесрочные модели (4—7 лет) обычно преследуют цель отразить результаты влияния социально-экономической политики государства на наиболее важные показатели развития СЭС. Это поможет правительству количественно оценить разные направления в социально-экономической политике и определить лучший вариант с точки зрения общественного благосостояния. Могут быть представлены и более конкретные цели. Например, в среднесрочной модели Японии ставятся такие цели: — объяснение движения цен;
2. После определения целей прогнозирования разрабатывается схема причинно-следственных связей в моделях. Это позволяет определить необходимый набор регрессионных уравнений и тождеств, комплекс экзогенных и эндогенных факторов, в том числе управляющих и управляемых, определить алгоритм прогнозных расчетов, взаимосвязи между показателями развития СЭС страны. Эту схему можно назвать и логико-информационной, потому что она отражает логику прогнозирования и информационные взаимосвязи между блоками модели и отдельными ее уравнениями. При этом структурные (функциональные) уравнения и тождества должны сопрягаться со структурой системы национальных счетов. Например, в модели Японии 20-летнего периода упреждения для прогнозирования ВНП применяется производственная функция, а для прогнозирования общего объема капитала используется функция сбережений. Предложение рабочей силы определяется, вернее, задается экзогенно. Вводится параметр, характеризующий уровень технического прогресса в широком смысле как функция времени (/). Другая специфика модели заключается в том, что весь капитал распределяется также экспертным методом (экзогенно) между частными и государственными секторами, при этом в производственной функции используется только частный основной капитал, а также в том, что чистый экспорт определяется также экзогенно. Каждая модель имеет свою специфику, которая определяется особенностями страны, подходом той или иной группы прогнозистов к решению задач прогнозирования, их опытом и искусством (см. подробнее гл. 6). 3. Далее, получив систему функциональных уравнений и тождеств, отражающих взаимосвязи между показателями развития СЭС, с помощью аппарата корреляционно-регрессионного анализа определяются коэффициенты регрессии (а1) при факторах-аргументах уравнений, т.е. данная ЭКМ решается путем использования метода наименьших квадратов или других более сложных и точных методов. С этой целью вначале определяется прогнозное значение экзогенной переменной (в случае однофакторного уравнения) или экзогенных переменных (в случае многофакторного уравнения), которые являются факторами для определения первого эндогенного (вычисляемого посредством моделирования) переменного. Далее значение этого эндогенного переменного используется как фактор для второго уравнения регрессии. Если кроме этого фактора во втором уравнении имеются и экзогенные факторы, то опять прогнозируются их значения и используются для расчета второго уравнения. Таким образом решается вся система уравнений ЭКМ. Первый фактор (фактор первого уравнения) обычно выбирается из тех существенных факторов развития, которые изменяются достаточно «плавно» и его можно определить методом экстраполяции тренда. Другим подходом к выбору первого фактора является его значимость для развития СЭС, когда его значение в прогнозируемом периоде является определяющим, и поэтому оно может быть интерпретировано как цель развития. Другими словами, значение первого экзогенного показателя как цели (норматива) прогнозист устанавливает на основании гипотезы развития СЭС. Например, решение ЭКМ может начинаться с гипотезы, что ВНП страны будет расти в течение прогнозного периода на 3% в год. В долгосрочной модели Японии на 20-летний период в качестве такого фактора был определен ВНП страны. Но в качестве первой переменной может быть использована и так называемая предопределенная переменная (показатель развития предыдущего года по отношению к прогнозному году). Например, в долгосрочной модели Японии на 10-летний период упреждения ВНП определяется эндогенно, а экзогенными показателями послужили площадь обрабатываемой земли, а также такие показатели, как частный капитал в сельском хозяйстве и частный капитал в перерабатывающих отраслях за предыдущий год по отношению к прогнозируемому. 4. На следующей стадии определяется так называемый доверительный интервал использования полученных результатов. 5. Далее проверяется степень адекватности модели изучаемому процессу (объекту) по годам предпрогнозного периода. Проверка проводится в два этапа. Вначале в уравнения модели вставляются значения факторов (эндогенных и экзогенных) определенного года предпрогнозного периода, данные стат. отчетности по которому были использованы в ретроспективной матрице (расчетного периода), затем решается система уравнений модели. Обычно проверку проводят по данным нескольких лет (желательно относительно спокойных, когда СЭС не испытывала особых потрясений). Допустим, в формировании ретроспективной матрицы в 2000 г. для прогнозирования периода 2001—2005 гг. были использованы данные до 1998 г. включительно. Ввиду того, что разработанная ЭКМ отражает тенденции развития СЭС именно в этом ретроспективном периоде, адекватность модели реальности проверяется по годам базового периода и обязательно по конечному, 1998 году. Это — проверка «ex-post базовая». Далее проводится проверка «ex-post внебазовая». С этой целью в модели используются данные статотчетности, полученные в январе—феврале 2000 г. за 1999 г., т.е. не участвующие в разработке ЭКМ. Возможна и проверка «ex-post внебазовая» по данным 2000 г., года предпрогнозного периода, когда формируются окончательные варианты прогноза. Для этого используются данные отчетности за I квартал 2000 г. и проводится оперативный прогноз на 9 месяцев 2000 г. Данные прогноза 2000 г. вводятся в прогнозную модель. По результатам проверок с участием экспертов проводится корректировка как самой модели, так и ее элементов, в особенности экзогенных факторов. В дальнейшем по истечении каждого года прогнозного периода с целью верификации используются отчетные данные этих лет. Такая проверка моделей называется «ex-ante». Схематически это представлено на рис. 3.3.   1   990 ex-post базовая 1999-2000 ex-ante 2005 990 ex-post базовая 1999-2000 ex-ante 2005            ретроспективный переходex-post   внебазовая внебазоваяпрогнозный период     допрогнозный период допрогнозный период Рис. 3.3. Различные периоды верификации прогнозов Важно помнить, что статистические модели хоть и позволяют получить качественную интерпретацию теоретических положений, но в силу вероятностного (стохастического) характера эти интерпретации не могут восприниматься как строгие доказательства или опровержения теоретических положений. Если имеется расхождение между теорией и результатами математических расчетов, то это скорее свидетельствует о некорректности математических расчетов. Обычно регрессионные уравнения, которые вступают в явное противоречие с экономической теорией, исключаются из ЭКМ. Кроме того, объектом пересмотра должны явиться и переменные экономической политики (инструментальные переменные). Такая процедура наиболее целесообразна в тех случаях, когда предполагается периодически пересматривать первоначальный план, т.е. сделать среднесрочный государственный план «скользящим», как можно ближе к действительности. Необходимость системы проверок основана на постулате: если модель не может удовлетворительно воспроизвести прошлое развитие (движение) системы, нет никаких оснований полагать, что она сможет воспроизвести будущее и ее можно использовать для прогнозирования. Но не надо забывать, что ЭКМ отражает тенденцию развития СЭС, т.е. она как бы «усредняет», «сглаживает» кривую развития СЭС в многомерном пространстве. Если расчетный (ретроспективный) период равен 10—15 годам и в последние годы тенденции развития существенно изменились, то ЭКМ этого не покажет. Проверка ЭКМ по последним годам предпрогнозного периода позволит выявить эти изменения. Если они носят стабильный, долговременный характер, связанный, например, с началом кризисной ситуации в стране, на мировом рынке или, наоборот, подъемом экономики (переходом СЭС из одной фазы развития в другую), то с использованием метода экспертных оценок необходимо изменение уравнений регрессии модели, вплоть до введения новых факторов развития со своими коэффициентами регрессии. Но в этом случае уже теряется грань между эконометрическими и имитационными моделями, которые будут рассмотрены ниже. Таким образом, при разработке эконометрических прогнозов, несмотря на то что в их основе лежит математическая модель, большую роль играет эффективное использование других методов прогнозирования, умение исследователя поставить достижения экономической теории на службу прогноза. Эконометрические прогнозы представляют собой синтез различных методов прогнозирования. Ввиду того что основу ЭКМ составляет система регрессионных уравнений, рассмотрим основные требования к ним. 1. Адекватность формы связи уравнения изучаемому объекту. Форма связи обычно задается самим прогнозистом в соответствии с его представлением об объекте прогнозирования, но также она может быть выбрана с использованием различных оценочных коэффициентов уравнения. Однако не всегда возможно использование линейной (аддитивной) формы связи, поэтому в ЭКМ различных стран часто используется и степенная (мультипликативная) форма связи. Например, широко известна производственная функция Кобба—Дугласа и его модификации. Желательно свести модель к линейной форме, так как весь аппарат корреляционно-регрессионного анализа ориентирован на линейность связей: Y = a0 + a1X1 + a2X2 + … + anXn Но если выбирается степенная связь типа: Y = a0X1a1+ X2a2 + … + Xnan то можно свести ее к линейной форме, логарифмируя: InY = In a0 + a1 In X1 + a2 In X2 + … + an In Xn 2. Существенность факторов-аргументов. Установление комплекса наиболее существенных факторов, влияющих на значение результирующего показателя (функции), в основном зависит от знаний прогнозиста или целой их группы и привлекаемых экспертов. Экономическая теория в силу своих возможностей дает представление о факторах, влияющих на значение различных макроэкономических показателей. Аппарат корреляционно-регрессионного анализа позволяет количественно оценить существенность каждого фактора как в абсолютном, так и относительном выражении (в процентах от общего влияния факторов).
Сначала для установления отсутствия мультиколлинеарности рассчитываются парные коэффициенты корреляции между всеми факторами попарно. Если линейная связь между двумя факторами достаточно тесная, то прогнозист по своему усмотрению оставляет один из факторов для дальнейшего исследования. Одни авторы считают, что если парный коэффициент корреляции ххixk< 0,6, то связь достаточно слабая и можно оставить для дальнейшего рассмотрения оба фактора, а другие — если ххjxk>0,3, то связь достаточно тесная и необходимо выбрать из двух факторов один. Ввиду того что определение «порогового» значения тесноты связи для установления мультиколлинеарности довольно субъективно, в качестве ее критерия может быть принято следующее соображение.
6. Соответствие уравнения регрессии стандартным требованиям.В этом случае оценка также проводится по соответствующим критериям корреляционно-регрессионного аппарата. Если уравнение не соответствует стандартным требованиям, оно должно быть скорректировано или исключено из ЭКМ. Рассмотрение особенностей эконометрических моделей позволяет сформулировать преимущества моделирования по сравнению с другими методами разработки прогнозов. В числе основных преимуществ выделим:
Благодаря использованию ЭВМ можно, во-первых, увеличивать размерность моделей, рассматривая одновременно все более тонкие экономические взаимосвязи. Важно отметить при этом, что модельные расчеты позволяют получать прогнозы не просто по большому количеству показателей (последнее возможно и на основе моделей временных рядов), а сбалансированные, взаимоувязанные в непротиворечивую систему. Это является одним из самых ярких преимуществ моделей. Если эксперты способны разработать непротиворечивые прогнозы, как правило, для нескольких показателей (опросы и обследования охватывают десятки переменных), то эконометрические модели в настоящее время позволяют без особого напряжения регулярно прогнозировать развитие огромного числа показателей (1—3 тыс. в рамках одной модели). Во-вторых, автоматизация расчетов открывает возможность разработки не только базового, наиболее вероятного прогноза, но также и альтернативных вариантов развития экономики с учетом изменений каких-либо внешних или внутренних условий. Многовариантность прогнозов повышает научный уровень социально-экономического прогнозирования в целом, так как позволяет оценивать не одну, а несколько наиболее вероятных траекторий развития. Такой подход не может быть реализован на основе использования временных рядов и экономических обследований, где для получения вариантов прогнозов необходимо вводить существенные изменения и корректировки. Многовариантные экспертные прогнозы встречаются чаще, но они не могут конкурировать с ЭКМ ни по количеству уравнений, ни по номенклатуре используемых переменных. Рассмотрим подробнее такое важное преимущество ЭКМ, как учет влияния внешнеэкономических факторов. Реальное развитие СЭС подвержено сильнейшему взаимодействию большого числа факторов, которые часто не могут быть описаны в рамках изучаемой модели. Так, например, при разработке макромоделей любой конкретной страны необходимо учитывать внешнеэкономические условия, которые, естественно, не определяются переменными, входящими в номенклатуру этой модели. В силу этого ряд переменных не может быть адекватно определен внутри моделей и, следовательно* должен вводиться в нее извне. От внешнеэкономической ситуации зависят прежде всего такие показатели, как экспорт товаров и капитала, миграция рабочей силы. Поэтому эти показатели обычно вводятся в модель экзогенно. Важной группой внешних переменных являются и те, которые зависят от неэкономических (политических, социальных и др.) факторов. В частности, динамика государственных расходов определяется не только требованиями эффективного развития, но в большей степени политическими устремлениями администрации. Учет этих устремлений в модели может быть осуществлен лишь посредством экзогенного использования факторов через внутреннее взаимовлияние модельных переменных. Необходимо отметить, что, обладая определенными преимуществами по сравнению с другими методами прогнозирования, эконометрические модели отнюдь не лишены недостатков. Являясь более удобным инструментом прогнозирования, они не разрешают и не могут разрешить его принципиальные проблемы. Прежде всего, модели не способствуют повышению точности прогнозирования поворотных точек развития. Они более пригодны для экстраполяции сложившихся тенденций развития, чем для распознавания изменений в них. По этой причине прогнозирование экономического роста на базе моделей возможно лишь посредством введения внешних переменных и различных корректировок параметров. Кроме того, сложность и неодназначность интерпритации результатов, требование соблюдения необходимой точности прогнозов усложняют их применение в реальных расчетах. Другим важным недостатком прогнозирования на базе эконометрических моделей является высокая стоимость таких исследований, требующих использования банков данных, ЭВМ, квалифицированных специалистов по разработке и эксплуатации этих моделей. Имитационная модель В социально-экономических исследованиях довольно широко распространен метод прогнозирования слабо структурированных проблем, причинно-следственные связи которых недостаточно изучены для построения удовлетворительной теории. В таком случае используется метод имитационного моделировании Социально-экономическая система любой страны из-за большого количества факторов, участвующих в описании ее функционирования, тем более в условиях постиндустриальной фазы, усложняющей связи между факторами, вызывающими нестабильность и неопределенность ее развития, является объектом со слабо структурируемыми связями. Поэтому для исследования и прогнозирования таких объектов строится система математических зависимостей, необязательно вытекающих из строгих теоретических предпосылок. С помощью определенных формальных приемов эта система математических зависимостей идентифицируется с реальным объектом. Убедившись в том, что построенная система воспроизводит хотя бы часть свойств реального объекта, на вход системы подают воздействия, характеризующие внешние условия (например, экзогенные факторы и управляющие, в том числе инструментальные переменные), и получают (снимают) последствия этих воздействий на выходе системы. Таким образом получают варианты поведения модели объекта. Если объектом изучения является некоторая переменная Y, то строится модель, в основе построения которой лежит предположение, что на Yвоздействует Xвектор, составленный из определенного количества переменных kв соответствии с функциональным соотношением: Y=f(X). Частным случаем функционального соотношения между Yи Xявляется простая линейная модель: k Y   = Qi Xi , = Qi Xi ,  i=1 где Qi— некоторые параметры. Модель можно сделать еще более реалистичной (и тем самым более сложной), если включить в нее нелинейные зависимости между Yи X, а также случайные величины, каждую со своим весом и своей функцией распределения в зависимости от времени. Дальнейшее усложнение модели связано с введением логических переменных, разного рода ограничений, запаздываний, описывающих механизм обратной связи. Ясно, что такую модель нельзя исследовать аналитическими методами. Поскольку имитационные модели могут учитывать и неформализованные связи и характеристики прогнозируемой системы, они способны наиболее адекватно отобразить ее развитие. Однако именно описание таких неформализованных характеристик и представляет основную трудность при построении имитационных моделей. Особенно важно, что динамические имитационные модели позволяют делать выводы об основных чертах развития системы, которые не зависят существенно от начальных условий. Эти выводы затем детализируются с помощью других методов прогнозирования. Имитационные модели предназначены для получения информации о моделируемой системе и выработки в последующем соответствующих оценок, пригодных для формирования решений. В качестве примера рассмотрим имитационную модель согласования производства и потребления в многоотраслевой экономике, представленную на рис. 3.4. Система имеет два формализованных блока: блок имитации материального производства и блок имитации сферы потребления. В системе предусмотрен экспериментатор, который может распоряжаться несколькими параметрами управления: распределением между отраслями капитальных вложений, темпами накопления, оплатой труда — зарплатоемкостью единицы продукции, оптовыми и розничными ценами. Экспериментатор         Распределение капиталовложений Темпы накопления Индексы оптовых цен Зарплатоемкость Индексы розничных цен      Блок имитации сферы материального производства Блок имитации сферы потребления      Данные анализа  Рис. 3.4. Структура имитационной модели Экспериментатор осуществляет активный диалог с ЭВМ. Используется информация о корректировочных показателях расчетного спроса на вид продукции и его конечного производства отраслью. Если показатель превышает единицу, значит, спрос на продукт выше предложения, если меньше единицы — то, наоборот. Корректировочные показатели и темпы роста валовой продукции по отраслям анализируются экспериментатором с позиции их допустимости. Если они нуждаются в изменении, экспериментатор может менять тот или иной параметр управления. Например, меняется распределение капиталовложений или совокупный доход населения (через отраслевые коэффициенты зарплатоемкости), или масштаб цен. Блоками определяются новые корректировочные показатели. Как только экспериментатор приходит к выводу о достижении удовлетворительного соотношения производства и потребления, он переводит систему к расчетам на следующий год. Таким образом, работа человеко-машинной имитационной системы позволяет находить варианты прогноза, обеспечивающие наилучшее соответствие между денежными доходами населения и объемами предлагаемых товаров и услуг. Варьирование управляющих параметров, оценка промежуточных и выбор окончательного решения возлагаются на экспериментатора, множество возможных вариантов решения рассчитывается на ЭВМ. Имитационная деловая игра представляет собой дальнейшее развитие имитационной системы и включает наряду с основными ее элементами (имитационной моделью и средствами анализа и обработки результатов имитации) специальные инструктивные и другие средства, которые регламентируют воздействия экспертов-экспериментаторов, являющихся в игре лицами, принимающими решения и заинтересованными в достижении наилучших результатов функционирования моделируемой системы в будущем. Игрокам должна предоставляться возможность осуществлять в произвольные моменты времени запрос информации из широкого класса данных. При создании игровой имитационной модели следует прежде всего разработать систему мотивации игроков и сценарий игры: описание ролей при этом содержится в должностных инструкциях. Часть моделей такого рода рассчитана на использование компьютеров, часть — на безмашинную имитацию. Игровые имитационные модели могут строиться для объектов любого уровня: от участка цеха до СЭС. Создание хорошей модели требует больших затрат времени (до нескольких лет) и обходится недешево, прогнозирование с ее помощью, т.е. проведение игры, также требует серьезных усилий, так как число участников игры может доходить до нескольких сотен. Однако эти затраты оправданы, ибо такие модели дают возможность получить прогноз там, где никакой другой метод не работает. Имитационное моделирование имеет ряд преимуществ:
сравнительно легкое отражение динамики процессов, временных параметров, сроков, запаздываний. Процесс прогнозирования на основе имитационного моделирования состоит из нескольких основных этапов: 1. Постановка задачи исследования, изучение прогнозируемой системы, сбор эмпирической информации, выделение основных проблем моделирования.
В имитационном эксперименте основной задачей каждого участника является конструирование из возможных вариантов некоторой стратегии, обеспечивающей достижение наилучших результатов. Вопросы для самоконтроля
3.4. Факторы, определяющие выбор метода прогнозирования Выбор метода прогнозирования, с одной стороны, должен обеспечить функциональную полноту, достоверность и точность прогноза, а с другой — уменьшить затраты времени и средств на прогнозирование. Актуальность разработки формальных, в том числе логических, процедур выбора типа или непосредственно метода прогнозирования возрастает под воздействием трех групп причин. Первая группа причин связана с большим числом методов прогнозирования, порождаемым разнообразием практических задач прогнозирования. В настоящее время количество методов прогнозирования насчитывается свыше двух сотен. Поэтому даже краткое ознакомление с известными методами прогнозирования путем простого перебора потребует немало времени и сил. Вторая группа причин состоит в том, что постоянно возрастает сложность как самих решаемых задач, так и объектов прогнозирования. В особенности это относится к современным СЭС. Третья группа связана с возрастанием динамичности (подвижности) СЭС. Прогнозист должен в результате предпрогнозных исследований структурировать информацию об объекте прогнозирования, проанализировать ее и принять решение о том, какой из методов в большей степени соответствует конкретным условиям прогноза. При этом важно на этапе подготовки решения о выборе метода прогнозирования выделить как методы, применение которых возможно в условиях решаемой задачи, так и те, которые применять нельзя. Последние исключаются из числа рассматриваемых альтернатив. Выбор метода прогнозирования не может быть предметом субъективных склонностей прогнозиста или группы прогнозистов и должен определяться в соответствии с объективными критериями выбора. Критериями выбора метода являются:
Проблемы различаются по степени развитости и четкости связей между исследуемыми проблемами и их следствиями; выделенными факторами и результативным показателем. Выделяют четыре класса проблем, имеющих место при решении прогнозных задач.  1. Стандартные проблемы. Связи между фактором и результатом строго детерминированы, они могут быть выражены функциональными уравнениями, простым расчетом (например, производительность труда равна отношению объема производства в неизменных ценах на численность работающих). 1. Стандартные проблемы. Связи между фактором и результатом строго детерминированы, они могут быть выражены функциональными уравнениями, простым расчетом (например, производительность труда равна отношению объема производства в неизменных ценах на численность работающих).2. Структурированные проблемы. Связи носят вероятностный (стохастический) характер, но отличаются высокой степенью тесноты. При изменении факторов результат может определяться с некоторым интервалом «от» и «до», но может определяться и однозначно (например, определение темпов роста производительности труда в зависимости от темпов его фондовооруженности).
Важно иметь в виду, что класс проблем зависит от объекта прогнозирования. Так, например, ясно, что прогнозирование развития науки и техники по своей сути относятся к слабо структурированным проблемам, в отличие, например, от прогнозирования развития производства. Но это в общем случае. В то же время интервал упреждения, т.е. период прогнозирования, может изменить класс проблем для одного и того же объекта. Так, прогнозирование изменения объема основных производственных фондов в зависимости от объема инвестиций в краткосрочном периоде (1 год) относится к структурированным проблемам (2 класс), а та же проблема, решаемая в долгосрочном периоде (до 10 лет), переходит в класс слабо структурированных проблем (3 класс), а в долгосрочном периоде на 20 лет и тем более в дальнесрочном периоде (свыше 20 лет) — в класс неструктурированных проблем. В случае, если проблема решается на уровне организации (фирмы) в краткосрочном периоде, она может быть отнесена к стандартным проблемам (например, расчет производственной мощности при наличии информации о вводе и выводе мощностей в прогнозируемом году). Также ее можно отнести к слабо структурированным и даже не структурированным проблемам по мере удлинения периода прогнозирования (интервала упреждения) и повышения уровня управления (например, региональный, отраслевой или федеральный). Таким образом, при переходе на более высокий уровень управления и увеличении периода упреждения степень структурированности проблемы уменьшается. Для прогнозирования стандартных проблем используются тождества (равенства) и экономико-математической модели. Для структурированных проблем применяются эконометрические и экономико-математические модели. Для слабо структурированных проблем — методы экспертных оценок, метод сценария, возможно использование и эконометрических моделей. Для неструктурированных проблем — в основном логические методы, методы экспертных оценок с высокой степенью агрегирования переменных, а также имитационные модели. Вопросы для самоконтроля
|
