Прогнозирование Парсаданов. Программа Культура России
 Скачать 2.29 Mb. Скачать 2.29 Mb.
|
|
6.3. Опыт разработки эконометрических моделей в системе прогнозирования Японии Долгосрочная макромодель I Японии с двадцатилетним периодом упреждения Цели прогнозирования модели I: 1) выявление перспективы роста социально-экономической системы Японии на столь долгий срок, на какой только это возможно; 2) исследование тенденций таких компонентов, как общественный капитал и частные инвестиции в жилищное строительство. Установление их связи с общим ростом экономики, так как эти связи нельзя достаточно точно изучать при помощи среднесрочной модели из-за длительных периодов формирования и действия этих компонентов. Информация формировалась на основе данных по годам системы национальных счетов по блоку национальный доход, выраженный в неизменных ценах (т.е. физическом выражении). Метод оценки модели I — метод наименьших квадратов. Общая упрощенная схема дана на рис. 6.1. Используя ВНП (V) как экзогенный фактор, были рассчитаны валовые сбережения (S), т.е. средняя доля сбережений в ВНП как сумма частных и государственных сбережений. Функция сбережений: S = a0 + a1 V. Затем была определена функция частных инвестиций в жилищное строительство (Ih) в зависимости от ВНП: In Ih= - In a0+ a1 In V. Быстрый рост инвестиций в жилищное строительство дало значение а1= 1,21 ВНП (V)    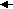 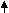 Частный основной капитал без учета износа, исключая жилища (Kp) 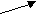 Kp-1 Частные инвестиции в возмещение выбытия основных фондов (Rp) 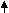  Отдельно lp Отношение lp lg B (экзогенно) Отдельно lg      Частные инвестиции в ОФ на частных предприятиях + валовые гос. инвестиции в ОФ (lp + lg) (зная lh , через тождество валовых сбережений получаем lp+ lg)   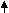 Чистый экспорт товаров и услуг, включая доходы, поступающие из-за границы – экогенно (B) Валовые сбережения ( S* ) Валовые затраты на индивидуальное жилищное строительство ( lh ) ВНП (V) 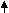 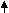  Рис. 6.1. Причинно-следственные связи в долгосрочной модели Методом экспертных оценок был определен чистый экспорт товаров и услуг, включая доходы, поступающие из-за границы (В). Было использовано тождество: S = Ip + Ig + Ih + B, где S— валовые сбережения; 1Р— валовые инвестиции в ОФ на частных предприятиях; 1g— валовые государственные инвестиции в ОФ; Ih — валовые частные инвестиции в жилищное строительство; В — чистый экспорт товаров и услуг. Используя значения Ihи В, рассчитана сумма IP + Ig, т.е. общий объем государственных и частных инвестиций в ОФ. Для расчета отдельно 1Ри Igметодом экспертных оценок была определена переменная B как отношение 1Р к Ig Ip B  = . = .Ig Используя значения валовых инвестиций в ОФ на частных предприятиях (Ip) как фактор, определили функцию частных инвестиций в возмещение выбытия ОФ (реновацию): Rp = a0 + a1Ip . Использую тождество Kp = Kp-1 + Ip + Rp , где Кр— частный основной капитал без учета износа, исключая затраты на жилищное строительство Ih; Кp-1— то же, за прошлый год; зная 1Ри Rpи объем частного основного капитала за прошлый год (Кр-1), определили Кр. В результате ВНП прогнозируется как функция от частного основного капитала. Точнее, в долгосрочном периоде производственная функция определяется как функция потребности в основных фондах: In V = - а0+ а1In Kp + a2t, где t— фактор времени. Долгосрочная макромодель II Японии с десятилетним периодом упреждения Цели те же, что и у модели I. Однако есть некоторые отличия: — во-первых, данная модель является двухсекторной (сектор 1 — отрасли первичного производства, включая сельское хозяйство, лесное хозяйство и рыболовство; сектор 2 — перерабатывающие отрасли) и предназначается для исследований тенденций изменения макроэкономических показателей по секторам и изменения их роли в экономике;
Эта модель роста состоит из 2-х блоков: а) I блок основывается на производственной функции и определяет ВНП; б) II блок основан на функции сбережений и позволяет установить чистые инвестиции. Рассмотрим структурные уравнения модели. Определяется производственная функция для I сектора как функция площади обрабатываемой земли, приходящейся на одного занятого в сельском, лесном хозяйстве и   AKp1 AKp1Рыболовстве — и капиталовооруженности одного занятого —— предыдущего года. L1L1 Производственнаяфункция представлена производительностью труда одного занятого: V1 A (K p1)-1 In _____ = a0 + a1In _____ + a2 In ________ + a3 t. L1 L1 L1 Производственная функция определяется в форме производительности труда по перерабатывающим отраслям (II сектор) как функция от капиталовооруженности одного занятого предыдущего года: V2 (K p2)-1 In _____ = __ a0 + a1In ________ + a2 t. L2 L2 Определяется функция распределения трудовых ресурсов между I и II секторами экономики: L1 V2 In _____ = __ a0__ a1In _____. L2 L2 Специфика Японии в период ретроспективного анализа заключалась в том, что наблюдался излишек трудовых ресурсов в первичном секторе. Поэтому вначале определялась занятость во II секторе — перерабатывающей промышленности, а затем по разнице между общей численностью работающих и занятостью в перерабатывающих отраслях определялась занятость в первичном секторе. Далее, как и в I модели, определяются инвестиции в частное жилищное строительство и объем валовых сбережений (S) как функция от ВНП (V): In Ih = __ a0In V , S = __ a0 + a1V . Определяется потребление продовольственных продуктов (Q) как сумма валовой добавленной стоимости в I секторе (V\) и импорта продовольственных продуктов (Mj) как функция от валовых расходов (V-S). In Cf = a0 + a1In (V __ S) Импорт производственных товаров (Mj) равен разности между общим потреблением продовольствия и производством первичного сектора. Определяется индекс объема производства в перерабатывающих отраслях: O = __ a0 + a2V2 . Определяется функция импорта (Мо) как функция от индекса объема производства во II секторе (О). Так как импорт продовольственных продуктов (Mf) определен в составе потребления продовольственных продуктов (Сf), то здесь определяется прочий импорт товаров народного пользования и услуг: M0 = a0 __ a1O . Уменьшение (-а1О) предельной склонности к импорту по отношению к индексу объема производства в перерабатывающих отраслях указывает на тенденцию к замене импорта товарами отечественного производства. Определяется функция экспорта товаров и услуг (Е) как функция от мирового экспорта Тwв млрд. долл. и производительности труда в перерабатывающих отраслях: V2 In E = __ a0 + a1 In Tw + a2In ___ . L2 Далее, как и в модели I, определяются частные инвестиции в возмещение выбытия ОФ (Rp) как функция от валовых частных инвестиций в ОФ (1п), значение которой берется из модели I (через экзогенный коэффициент B): Rp = a0 + a1 Ip. Далее определяется функция распределения капитала в перерабатывающих отраслях (Кр1) как объем частного капитала без учета амортизационных отчислений (т.е. чистых инвестиций), исключая частные инвестиции в жилищное строительство: Kp2 = __ a0 + a1 Kp . Объем частного капитала в I секторе (Кп1) определяется как разница между Кр, т.е. общим объемом частного капитала без учета амортизационных отчислений и частных затрат на жилищное строительство, полученным по тождеству в модели I: Kp1 = Kp __ Kp2 . Поэтому коэффициент регрессии а1можно трактовать как параметр, в определенной степени выражающий экономическую политику государства (структурную, инвестиционную), и изменять его величину при совершенствовании модели. Тождества, используемые в модели II, следующие: L = L1 + L2(Lзадается экзогенно); V = V1 + V2; Cf = V1 + Mf ; M = M0 + Mf; B = E__M; S = Jp + Jg + Jh + B; Kp= (Kp)-1 + Jp__Rp; Kp = Kp1 + Kp2. Среднесрочная модель Японии Ее цели:
Разработка проводилась как в неизменных, так и текущих ценах. Для того чтобы связать текущие затраты с уровнем реальных затрат (расходов), или реальным эффективным спросом, а также уровнем производства и занятости, были введены шесть коэффициентов пересчета текущих цен в неизменные: индексы потребительских цен, цен на инвестиционные товары, стоимости жилищного строительства, оптовых цен, цен экспортных товаров и цен импортных товаров. Все пять коэффициентов пересчета определяются эндогенно, а цены импорта — экзогенно. Эффективный спрос в неизменных ценах подразделяется по различным секторам экономики при помощи межотраслевой модели и таким образом он непосредственно связывается с объемами производства и импорта по 60 отраслям, а также с занятостью и объемом капитала по 25 секторам национальной экономики. Среднесрочная модель содержит 24 структурных уровня и 19 тождеств. Период ретроспективного анализа охватывает 20 полугодовых интервалов между финансовыми годами (с 1 апреля). Важной чертой модели является присутствие в ней нелинейных структурных уравнений, которые затем решаются без какого-либо приведения их к линейной форме. Нелинейность является неизбежным следствием попытки ввести в макромодель механизм связи между заработной платой и ценами. Модель, как мы знаем, можно решить аппроксимизацией (заменой) нелинейных соотношений линейными (через логарифмирование), но наивысшую точность дает метод, при котором нелинейность сохраняется и для решения модели используется метод итерации. В связи с использованием итерационного процесса пришлось все уровни модели разбить на 3 блока: I блок — содержит систему линейных уравнений; II блок — содержит только нелинейные уравнения, которые решаются итерационным способом; III блок — содержит нелинейные уравнения, которые решаются методом аппроксимации. В I блоке определяется сумма валовых национальных расходов в неизменных ценах и ее компоненты как функции от распределения дохода в предшествующем периоде, объема внешней торговли и расходов правительства в прогнозируемом (текущем) периоде. Во II блоке находятся цены, заработная плата, занятость. В III — уровень распределенных доходов в текущих ценах. Расчеты проводятся для каждого года прогнозируемого периода (скользящее прогнозирование), что позволяет получить ряд эндогенных переменных, используемых для последующего расчета. Межотраслевая модель Японии С ее помощью в среднесрочном государственном плане были определены плановые показатели по секторам. Модель преследует две основные цели. Первая цель — дать каждому сектору оценку спроса на продукцию, импорта, занятости и капиталу на конец пятилетки, согласованную с реальными совокупными оценками расходов, полученными на основе среднесрочной макромодели. Вторая цель — контроль в разбивке по секторам прогнозируемых величин индексов промышленного производства, импорта, занятости и валовых частных инвестиций, исчисленные с помощью межотраслевой модели. Первая цель обусловлена тем, что среднесрочная макромодель служит лишь целям анализа изменений в общих расходах или в отдельных статьях спроса на конечную продукцию, но не устанавливает связи с изменениями в спросе на промежуточную продукцию (промежуточном спросе) или межотраслевых потоках. Таким образом, среднесрочная макромодель не отражает проблемы деятельности секторов и изменения в отраслевой структуре национальной экономики. Поэтому межотраслевая модель дополняет среднесрочную макромодель в том смысле, что благодаря ей становится возможным довольно подробно анализировать все взаимосвязи, характерные для данной отраслевой структуры. Необходимая занятость и капитал по секторам получаются на основе функций спроса на рабочую силу и производственных функций, основывающихся на уровне заработной платы, полученном при помощи среднесрочной макромодели, и объемах продукции по секторам. При определении оценок — от структуры совокупного конечного спроса и до спроса по секторам и видам ресурсов, а также оценок потребностей в рабочей силе и капитале по секторам — проверяется их согласованность с помощью примерно семи тысяч структурных параметров. Рассматриваемая нами межотраслевая модель является статической открытой моделью В.В. Леонтьева, но имеющая некоторые характерные особенности, касающиеся разбивки конечного спроса, корректировки коэффициентов прямых затрат (щ) при прогнозах, оценки потребности в импорте по секторам, занятости, капитала. Система уравнений, упрощенная для иллюстративных целей, выглядит следующим образом. Конечный спрос по продуктам имеет вид: Fd i = Ci + Gi + Ii + Ji + Ei , (1) где С, — потребительские расходы, по видам продуктов; G/ — расходы (закупки) государства, по видам продуктов; // — валовые частные инвестиции (в основные фонды и индивидуальное строительство), по видам продуктов; J, — изменение запасов, по видам продуктов; Е, — чистый экспорт товаров и услуг, по видам продуктов Уравнение показывает, что реальные расходы по статьям конечного спроса делятся в макромодели по 60 секторам и при этом используются различные виды подмоделей (функция потребления, функция экспорта)    Xi + Mi = aij Xj + Fdi , (2) Xi + Mi = aij Xj + Fdi , (2) j jгде Xi— валовой выпуск, по отраслям; Мi — импорт товаров и услуг, по видам продуктов; аи— коэффициент прямых затрат; Fdi— конечный спрос на виды продукции. Уравнение (2) является уравнением баланса спроса и предложения и представляет собой центральное звено межотраслевой модели: левая сторона уравнения отражает предложение по некоторой группе продуктов, а правая — промежуточный и конечный спрос. В уравнении (3) используется функция, которая разделяет общее предложение продуктов на отечественное производство и импорт: M1 = f (Xi + Mi) , (3) Vi = viXi , (4) где Vi- валовая добавленная стоимость, по отраслям; vt— доля добавленной стоимости в объеме валовой продукции отрасли. Уравнение (5) дает возможность исчислить спрос на рабочую силу, исходя из добавленной стоимости и реальной ставки заработной платы: w Li = f(Vi , ____), (5) Pc где L, — занятость, по отраслям; реальная заработная плата одного занятого работника. Уравнение (6) позволяет сделать оценку спроса на капитал как функцию труда и добавленной стоимости: Vi = f (Ki, Li, t); (6) где К, —валовой капитал, по отраслям; t— время в календарных днях. Важным в межотраслевой модели В.В. Леонтьева является то, что в систему входят эконометрические подмодели, все экзогенные переменные исчисляются очень быстро при помощи ЭВМ большой мощности, и, наконец, то, что в модели учитываются мнения специалистов (экспертов) соответствующих отраслей. Интегрированная модель Японии Необходимость разработки этой модели объясняется следующими причинами. Первая группа причин:
Интегрированная модель комбинирует оба подхода моделей роста. Вторая группа причин:
Интегрированная модель учитывает систему «обратных связей» между среднесрочной макромоделью и межотраслевой моделью. Поскольку модель довольно сложна, охарактеризуем ее общую структуру и основные причинно-следственные связи. Модель состоит из трех блоков:
Рассмотрим содержание этих блоков. |
