диплом. Программа курса по выбору Математическая логика для школьников
 Скачать 0.8 Mb. Скачать 0.8 Mb.
|
|
Конспект занятия 7 по теме: «Логические задачи и методы их решений» Основная цель: познакомить обучающихся с различными методамирешения логических задач; формировать навыки и опыт решения логических задач. Планируемые результаты: Предметные: знание различных методов решения логическихзадач (метод рассуждений, метод таблиц, метод графов, метод решения с помощью языка математической логики); умение решать логические задачи различными методами. Метапредметные: умение самостоятельно планировать путидостижения учебных целей; способность осознанно выбирать наиболее эффективные способы решения учебных задач; владение языком математической логики; умение строить логические рассуждения и делать обоснованные выводы и умозаключения; навыки самоконтроля; коммуникативные навыки в ходе комментирования решений и ответов учащихся. Личностные: ценностное отношение к математическим знаниям;целеустремленность и увлеченность при решении математических задач; способность к логическим умозаключениям; готовность к самообразованию. 67 Этапы занятия: Постановка цели занятия Теоретическая часть. Дидактическая игра. Подведение итогов. Решали ли вы логические задачи? А чем они отличаются от обычных задач? Логические задачи от обычных отличаются тем, что не требуют вычислений, а решаются с помощью рассуждений. Эти задачи носят занимательный характер, поэтому они привлекают даже тех учащихся, которые не очень любят математику. В то же время дух математики в них чувствуется ярче всего - половина решения любой математической задачи (а иногда и гораздо больше половины) состоит в том, чтобы как следует разобраться в условии, распутать все связи между участвующими объектами. На сегодняшнем занятии, вы узнаете некоторые способы решения логических задач и научитесь применять их на практике. Можно выделить несколько различных способов решения логических задач: o o o Метод рассуждений; Метод таблиц; Метод графов; Остановимся отдельно на каждом из выделенных методов, иллюстрируя их примерами решения конкретных задач. Метод первый: Метод рассуждений 68 Идея метода состоит в том, что мы проводим рассуждения, используя последовательно все условия задачи, и приходим к выводу, который и будет являться ответом задачи. Этим способом обычно решают несложные логические задачи. Например. Возраст мамы и дочки в сумме составляет 98 лет. Дочь родилась, когда маме было 22 года. Сколько лет маме и дочке? Решение: так как разница в их возрасте 22 года (именно в этом возрасте у мамы родилась дочь), то 98 – 22 =76 (лет). Это удвоенный возраст дочери, тогда 76 : 2 = 38(лет). Значит, матери 98 – 38 = 60 (лет). Метод второй: Метод таблиц Основной прием, который используется при решении текстовых логических задач, заключается в построении таблиц. Таблицы не только позволяют наглядно представить условие задачи или еѐ ответ, но и в значительной степени помогают делать правильные логические выводы в ходе решения задачи. Идея метода: оформлять результаты логических рассуждений в видетаблицы. Преимущества метода: 1)наглядность; 2)возможность контролировать процесс рассуждений; 3)возможность формализовать некоторые логические рассуждения. Данным способом можно решить, известную многим загадку Эйнштейна: 5 разных человек в 5 разных домах разного цвета, курят 5 разных марок сигарет, выращивают 5 разных видов животных, пьют 5 разных видов напитков. Вопрос:1) Кто выращивает рыбок? 2)Норвежец живет в первом доме. 3)Англичанин живет в красном доме. 4)Зеленый дом находится непосредственно слева от белого. 5)Датчанин пьет чай. 69 6)Тот, кто курит Rothmans, живет рядом с тем, кто выращивает кошек. 7)Тот, кто живет в желтом доме, курит Dunhill. 8)Немец курит Marlboro. 9)Тот, кто живет в центре, пьет молоко. 10)Сосед того, кто курит Rothmans, пьет воду. 11)Тот, кто курит Pall Mall, выращивает птиц. 12)Швед выращивает собак. 13)Норвежец живет рядом с синим домом. 14)Тот, кто выращивает лошадей, живет в синем доме. 15)Тот, кто курит Philip Morris, пьет пиво. 16)В зеленом доме пьют кофе. Ответ:
Метод четвертый: метод графов. Граф -множество точек,изображенных на плоскости(листе бумаги,доске), некоторые пары из которых соединены отрезками. Точки называют вершинами графов, а отрезки - ребрами графов. Выделяя из словесных рассуждений главное - объекты и отношения между ними, графы представляют изучаемые факты в наглядной форме. Примеры решения логических задач с использованием графов подкупают своей наглядностью и простотой, избавляют от лишних рассуждений, во многих случаях сокращают нагрузку на память. С одной стороны, графы позволяют проследить все логические возможности изучаемой ситуации, с другой, благодаря своей обозримости, помогают в ходе решения задачи классифицировать логические возможности, 70 отбрасывать неподходящие случаи, не доводя до полного перебора всех случаев. Идея метода: выявление и последовательное исключение логическихвозможностей, задаваемых условиями задачи. Решим следующую задачу: Четыре футбольных команды: итальянская команда «Милан», испанская – «Реал», российская – «Зенит», английская – «Челси» встретились в групповом этапе лиги чемпионов по футболу. Их тренировали тренеры из этих же четырех стран: итальянец Антонио, испанец Родриго, русский Николай, англичанин Марк. Известно, что национальность всех четырех тренеров не совпадала с национальностью команд. Требуется определить тренера каждой команды, если известно: а) Зенит не тренируется у Марка и Антонио. б) Милан обещал никогда не брать Марка главным тренером. Решение: Исходя из условий задачи,получаем следующий граф. 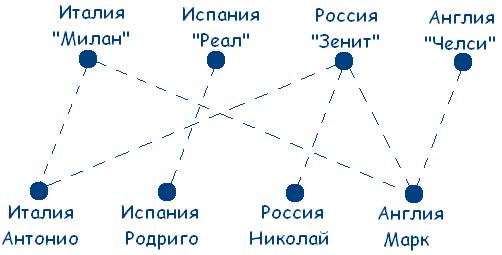 Сразу можем сделать вывод, что российская команда «Зенит» тренируется у испанца Родриго. Чертеж примет вид: 71 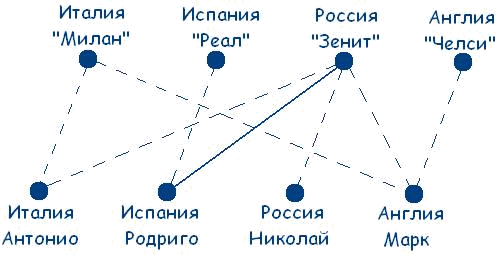 Теперь получили, что итальянская команда «Милан» тренируется у русского Николая. Внесем и эти изменения в чертеж, получим: 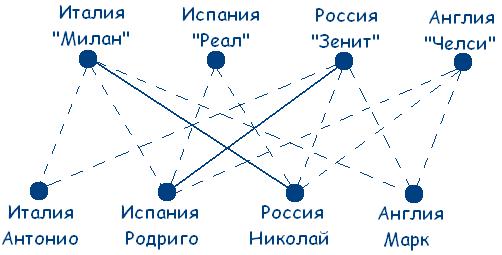 Приходим к выводу, что английская команда «Челси» тренируется у итальянца Антонио и испанская команда «Реал» тренируется у англичанина Марка. Ответ: Российская команда«Зенит»тренируется у испанца Родриго;итальянская команда «Милан» тренируется у русского Николая; английская команда «Челси» тренируется у итальянца Антонио; испанская команда «Реал» тренируется у англичанина Марка. Метод пятый: С помощью языка математической логики. Алгоритм применения метода: требуется выделить элементарныевысказывания, осуществить перевод на язык математической логики, составить формулы в соответствии с условием задачи, составить таблицу истинности и сделать вывод. Для примера решим следующую задачу: 72 По обвинению в ограблении перед судом предстали Иванов, Петров, Сидоров. Следствием установлено: если Иванов не виновен или Петров виновен, то Сидоров виновен; если Иванов не виновен, то Сидоров не виновен. Вопрос - виновен ли Иванов? Решение: Рассмотрим простые высказывания: А = «Иванов виновен», В = «Петров виновен», С = «Сидоров виновен».
Решить данную задачу — значит указать, при каких значениях А полученное сложное высказывание F истинно. Для этого необходимо проанализировать все строки таблицы истинности, где F = 1. И если хотя бы в одном из таких случаев А = 0 (Иванов не виновен), то у следствия недостаточно фактов для того, чтобы обвинить Иванова в преступлении. 73 Анализ таблицы показывает, что высказывание F истинно только в тех случаях, когда А истинно, т. е. Иванов в ограблении виновен. Ответ: Иванов–виновен. Решим эту задачу с помощью рассуждений. Предположим, что Иванов не виновен в преступлении, тогда выполняется условия 1 и 2. По условию 2 получается, что Сидоров не виновен. Получается противоречие. Следовательно, Иванов виновен, а про остальных нельзя сказать ничего определенного. Для дальнейшей работы, вам нужно будет разбиться на 2 команды. Каждой команде выдаются тексты с задачами. Задачи вы можете решать в произвольном порядке, любым из способов которые мы сегодня рассмотрели. За каждую правильно решенную и доступно изложенную задачу, команде засчитывается 5 баллов. В конце занятия подведем итоги. Задачи для игры: Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: "Вадим изучает китайский, Сергей не изучает китайский, Михаил не изучает арабский". Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей? Решение: Имеется три утверждения: Вадим изучает китайский; Сергей не изучает китайский; Михаил не изучает арабский. Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение ложно. Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно. 74 Остается считать верным третье утверждение, а первое и второе — ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей. Ответ: Сергей изучает китайский язык,Михаил—японский,Вадим — арабский. В симфонический оркестр приняли на работу трѐх музыкантов: Брауна, Смита и Вессона, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе. Известно, что: Смит – самый высокий Играющий на скрипке меньше ростом играющего на флейте Играющие на скрипке и флейте и Браун любят пиццу Когда между альтистом и трубачом возникает ссора, Смит мирит их Браун не умеет играть ни на трубе, ни на гобое На каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами? Решение: Составим таблицу и отразим в ней условия задачи,заполнивсоответствующие клетки цифрами 0 и 1 в зависимости от того, ложно или истинно соответствующее высказывание. Так как музыкантов трое, инструментов шесть и каждый владеет только двумя инструментами, получается, что каждый музыкант играет на инструментах, которыми остальные не владеют. Из условия 4 следует, что Смит не играет ни на альте, ни на трубе, а из условий 3 и 5, что Браун не умеет играть на скрипке, флейте, трубе и гобое. Следовательно, инструменты Брауна - альт и кларнет. Занесем это в таблицу 1, а оставшиеся клетки столбцов "Альт" и "Кларнет" заполним нулями. Таблица 1
75
Из таблицы 1 видно, что на трубе может играть только Вессон. Из условий 1 и 2 следует, что Смит не скрипач. Так как на скрипке не играет ни Браун, ни Смит, то скрипачом является Вессон. Оба инструмента, на которых играет Вессон, теперь определены, поэтому остальные клетки строки "Вессон" можно заполнить нулями. Таблица 2
Из таблицы 2 видно, что играть на флейте и на гобое может только Смит. В результате получим таблицу 3. Таблица 3
Ответ: Браун играет на альте и кларнете,Смит-на флейте и гобое,Вессон-на скрипке и трубе. Трое мальчиков имеют по некоторому количеству яблок. Первый мальчик дает другим столько яблок, сколько каждый из них имеет. Затем второй мальчик дает двум другим столько яблок, сколько каждый из них теперь имеет; в свою очередь и третий дает каждому из двух других столько, сколько есть у каждого в этот момент. После этого у каждого из мальчиков оказывается по 8 яблок. Сколько яблок было у каждого мальчика в начале? Решение: Решаем задачу с конца с помощью таблицы
Таким образом, первоначально яблок у первого, второго и третьего мальчиков было соответственно 13, 7 и 4. Ответ: 13яблок, 7яблок, 4яблока Однажды черт предложил бездельнику заработать. ―Как только ты перейдешь через этот мост, – сказал он, – твои деньги удвоятся. Можешь переходить по нему сколько хочешь раз, но после каждого перехода отдавай мне за это 24 рубля‖. Бездельник согласился и после третьего перехода остался без денег. Сколько денег у него было сначала? Решение: Так как после третьего перехода у бездельника денег неосталось, то после перехода моста в третий раз у него было 24 рубля, а до перехода третьего моста – 12 рублей. Тогда после перехода второго моста у бездельника было 12 + 24 = 36 (рублей), а до перехода второго моста – 36 : 2 18 (рублей). Рассуждая аналогично, получим, что после перехода первого моста у бездельника стало 18 + 24 = 42 (рубля), а перед переходом первого моста – 42 : 2 = 21 (рубль). Таким образом, у бездельника сначала был 21 рубль. Ответ: 21рубль. 5)Из поврежденной книги выпала часть сшитых вместе листов. Номер первой выпавшей страницы - 143. Номер последней страницы записан теми же цифрами, но в ином порядке. Сколько страниц выпало из книги? Решение: Первая выпавшая страница имеет нечетный номер. Следовательно, номер последней выпавшей страницы четный и равен 314 (единственное четное число, большее 143 и составленное из тех же цифр). В книге осталось 142 страницы, предшествующие выпавшим. Поэтому число выпавших страниц равно 314 - 142 = 172. Ответ: 172. 77 качестве итогового контроля в конце курса можно предложить учащимся пройти тест в компьютерной среде Geogebra. Примеры заданий:  78  79 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
