диплом. Программа курса по выбору Математическая логика для школьников

• Название: Программа курса по выбору Математическая логика для школьников
• Анкор: диплом
• Дата: 15.02.2021
• Размер: 0.8 Mb.
• Имя файла: диплом.docx
• Тип: Программа курса; #176550
• страница: 7 из 10

Конспект занятия 4 по теме:
«Логическое следствие»
Основная цель: познакомить учащихся с понятием«логическоеследствие» и методами его установления; формирование умений определять логическое следствие.
Планируемые результаты:
Предметные: знание определения понятия«логическоеследствие»; умение приводить примеры логического следствия; знание
54
основных свойств отношения «логическое следствие» (метод дедукции); знание основных логических правил вывода: закон контрапозиции и метод доказательства «от противного».
Метапредметные: владение языком математической логики;умение анализировать и обобщать изучаемые факты; умение строить логические рассуждения и делать обоснованные выводы и умозаключения; навыки планирования и организации учебно-познавательной деятельности; навыки самоконтроля; коммуникативные навыки в ходе комментирования решений и ответов учащихся.
Личностные: ценностное отношение к математическим знаниям;целеустремленность и увлеченность при решении математических задач; способность к логическим умозаключениям; готовность к самообразованию.
Этапы занятия:

1. 
   Постановка цели занятия
   

2. 
   Теоретическая часть
   

1. 
   На сегодняшнем занятии мы рассмотрим такое понятие как
   

«логическое следствие», а так же вы узнаете, каким методом пользуется знаменитый сыщик Шерлок Холмс.

2. 
   Одно из важнейших предназначений логики состоит в том, чтобы устанавливать, что из чего следует, т.е. устанавливать структуры высказываний, связанных отношением логического следования. Логическое следование относится к числу фундаментальных, исходных понятий логики,
   

которую нередко характеризуют как науку о том, «что из чего следует». Для обозначения логического следования формулы G из формул F₁, F₂ ,…, F_k используют следующее обозначение:
F₁, F₂ ,…, F_k ╞ G
Формула G(x₁, x₂, …, x_n) называется логическим следствием формул F₁(x₁, x₂,…, x_n), F₂(x₁, x₂,…, x_n),…, F_k(x₁, x₂,…, x_n), если она обращается в истинное высказывание при всяком наборе значений высказывательных
55

переменных x₁, x₂, …, x_n, при котором в истинное высказывание обращаются все формулы F₁,F₂, …,F_k
F₁, F₂, …, F_k ╞ G , где F₁, F₂, …, F_k - посылки для логического следования G, а G – заключение или логическим следованием формул F₁, F₂, …, F_k.
Если в таблице истинности формул F₁, F₂, …, F_k, G в какой-то строке все формулы F₁, F₂, …, F_k принимают значение «истина» и в этой строке непременно формула G принимает значение «истина», то это означает, что G является логическим следствием формул F₁, F₂, …, F_k. Иначе, не является
логическим следствием. Другими словами, отличительной чертой логического следования является то, что оно ведѐт от истинных высказываний только к истинным.
Из высказывания «Если натрий металл, он пластичен» логически вытекает высказывание «Если натрий не пластичен, он не металл», поскольку импликация, посылкой которой является первое высказывание, а следствием второе, представляет собой частный случай логического закона контрапозиции. (таблицы истинности для этих формул)
Закон контрапозиции –закон классической логики,утверждающий,что

• 
  том случае, если некая посылка А влечет некое следствие В, то отрицание этого следствия (то есть «не В») влечет отрицание этой посылки (то есть «не А»). На истинности закона контрапозиции основывается способ доказательства «от противного». Это такой вид доказательства, при котором доказательство некоторого суждения осуществляется через опровержение этого суждения.
  

Суть этого метода помогает понять загадка. Попробуйте еѐ разгадать.
«Представьте себе страну, в которой приговорѐнному к казни предлагается выбрать одну из двух одинаковых на вид бумаг: на одной написано «смерть», на другой — «жизнь». Враги оклеветали одного жителя этой страны. И, чтобы у него не осталось никаких шансов спастись, сделали так, что на обороте обоих бумажек, из которых он должен выбрать одну,

56

было написано «смерть». Друзья узнали об этом и сообщили осуждѐнному. Он попросил никому об этом не рассказывать. Вытащил одну из бумажек. И остался жить. Как ему это удалось?»
Осуждѐнный проглотил выбранную им бумажку. Чтобы установить, какой жребий ему выпал, судьи заглянули в оставшуюся бумажку. На ней было написано: «смерть». Это доказывало, что ему повезло, он вытащил бумажку, на которой было написано: «жизнь».
Решим следующую задачу, используя способ доказательства «от противного»:
Являются ли следующие рассуждения логически верными: «Если Джонс не встречал ночью Смита, то Смит был убийцей или Джонс лжет. Если Смит не был убийцей, то Джонс не встречал Смита этой ночью, и убийство имело место после полуночи. Если убийство имело место после полуночи, то Смит был убийцей или Джонс не лжет. Следовательно, Смит был убийцей».
Для этого введем логические переменные:
А: «Джонс не встречал ночью Смита»,
В: «Смит убийца»,
С: «Джонс лжет»,

4. 
   «убийство состоялось после полуночи».
   

Имеем посылки A→(B˅C), ¬B→(A˅D), D→(B˅¬C) и заключение В. Предположим, что t(A→(B˅C))=1, t(¬B→(A˅D))=1, t(D→(B˅¬C))=1,

• 
  t(В)=0.
  

t(¬B→(A˅D))=1 и t(¬B)=1 => t(A˅D)=1, t(A)=1, t(D)=1 t(A→(B˅C))=1 и t(A)=1 => t(B˅C)=1, т.к. t(В)=0, то t(C)=1 t(D→(B˅¬C))=1 и t(D)=1=>t(B˅¬C)=1,т.к. t(¬C)=0, то t(В)=1 Пришли к противоречию: t(В)=0, t(В)=1
Следовательно, предположение t(В)=0 неверно, а верно t(В)=1 и рассуждения логически правильны.

57

• 
  знакомы ли вы с таким персонажем как Шерлок Холмсом? Видели ли вы как гениальный сыщик, ведет расследование и разгадывает тайны? Все его догадки и размышления основываются на сугубо фактах, из которых Шерлок строит логическую цепочку, а она приводит его к разгадке. Так вот метод, который использует Шерлок Холмс, называется дедуктивным.
  

Понятие дедукция (лат. deductio – выведение) означает метод мышления, при котором частное положение логическим путѐм выводится из общего; цепь умозаключений (рассуждений), звенья которой связаны отношением логического следования.
Например: «Все металлы проводят ток. Золото — это металл. Значит, золото проводит ток».
Конспект занятия 5 по теме:
«Необходимые и достаточные условия»
Основная цель: познакомить учащихся с понятиями«необходимое идостаточное условие»; формировать умение определять необходимое и достаточное условие; развивать навыки составления теорем на основе различных логических структур.
Планируемые результаты:
Предметные: знание определений понятий«необходимое идостаточное условие»; умение определять необходимое и достаточное условие; умение формулировать математическое предложение (теорему) на основе различных логических структур.
Метапредметные: владение языком математической логики;навыки поиска и выделения необходимой информации; умение выстраивать аргументацию, приводить примеры и контрпримеры; умение строить логические рассуждения и делать обоснованные выводы и умозаключения; навыки планирования и организации учебно-познавательной деятельности; навыки самоконтроля; коммуникативные навыки в ходе комментирования решений и ответов учащихся.

58

Личностные: ценностное отношение к математическим знаниям;целеустремленность и увлеченность при решении математических задач; способность к логическим умозаключениям; готовность к самообразованию.
Этапы занятия:

1. 
   Теоретическая часть.
   

2. 
   Решение практических заданий.
   

3. 
   Подведение итогов.
   

1. 
   Представьте жизненную ситуацию: «Что бы Ваня поехал в Москву достаточно иметь деньги на поезд». Верно ли это утверждение? (Нет,
   

вместо «достаточно», надо «необходимо»)
«Достаточно ли, чтобы асфальт был мокрым, пошел дождь? (Да)
Если некоторое событие или факт не может иметь места без определенного условия, то это условие необходимо для осуществления указанного события или факта.
Если некоторое событие или факт обязательно имеет место при определенном условии, то наличие этого условия достаточно для осуществления этого события или факта.

• 
  необходимыми и достаточными условиями вы постоянно встречаетесь в геометрии, но возможно вы просто не знаете, что они так называются. А именно, необходимое условие есть свойство, а достаточное условие есть признак.
  

Многие теоремы в математике формулируются по следующей схеме: «Для любого элемента х ∈ Х из предложения p(x) следует предложение q(x)» или коротко: (∀х) p(x)→ q(x) (1), где знак следования (→) заменяет слова «откуда следует», «тогда», «если…, то…».
Часто запись (1) заменяют более короткой: p(x)→ q(x). Предложение p(x) называется условием теоремы,а предложение q(x) –заключениетеоремы.

59

Рассмотрим пример. В теореме Пифагора условие p(x) можно сформулировать так: «х – прямоугольный треугольник»; заключение q(x): «В треугольнике х сумма квадратов двух сторон равна квадрату третьей
стороны». Используя терминологию логики, теоремы можно сформулировать, так: «Если некоторый треугольник прямоугольный, то сумма квадратов двух его сторон равна квадрату третьей стороны».
Если теорема p(x)→ q(х) верна, то еѐ условие p(x) называют достаточным условием для заключения q(x),а заключение q(x) называют необходимым условием для p(x).
Например, теорема «Диагонали ромба взаимно перпендикулярны» верна, значит, еѐ условие p(x) «Четырѐхугольник х – ромб» является достаточным условием для заключения q(x) «Диагонали четырехугольника х взаимно перпендикулярны».
Таким образом, для того что бы диагонали четырехугольника были перпендикулярны, достаточно, чтобы этот четырехугольник был ромбом. Заключение этой теоремы q(x), является необходимым для условия этой теоремы p(x). Можно сказать, что, для того что бы четырехугольник был ромбом, необходимо, чтобы его диагонали были перпендикулярны.
Если верна не только теорема p(x)→ q(х), но и обратная ей q(х)→ p(x), то p(x) является необходимым и достаточным условием для q(х), а q(х) является необходимым и достаточным условием для p(x).
Например, верным являются как теорема Пифагора, так и ей обратная, поэтому сформулировать еѐ можно так: «Для того чтобы треугольник был прямоугольным, необходимо и достаточно, чтобы сумма квадратов двух его сторон была квадрату третьей».
Так же слова «необходимо и достаточно», заменяют на «тогда и только тогда», «в том и только в том случае», «те и только те».

2. 
   Выполним следующие задания:
   

1. 
   Выделить условие и заключение теоремы; сформулировать теорему, обратную данной:
   

60

1. 
   Если сумма цифр числа делится на 3, то и само число делится на 3;
   

2. 
   Каждый член арифметической прогрессии (начиная со второго) равен полусумме соседних с ним членов.
   

2. 
   Заменить многоточие словам «необходимо», «достаточно»
   

или «необходимо и достаточно» таким образом, чтобы получено утверждение было истинным:

1. 
   Для того чтобы сумма двух натуральных чисел делилась на
   

2,…, чтобы числа были четными.

2. 
   Для того чтобы число делилось на 9, …, что бы сумма его цифр делилась на 9.
   

2. 
   Для того чтобы числа х₁ и х₂ были корнями уравнения х²
   

+рх+q=0, …,что бы х₁ х₂ =q.
Ответы:

1. 
   1) «Сумма цифр числа делится на 3» – условие, «Число делится на 3» - заключение. Обратная теорема: «Если число делится на 3, то сумма цифр числа делится на 3.
   

2)«Последовательность является арифметической прогрессией» - условие, «каждый член (начиная со второго) равен полусумме соседних с ним членов» - заключение. Обратная теорема: «Если каждый член последовательности (начиная со второго) равен полусумме соседних с ним членов, то это последовательность является арифметической прогрессией.

2. 
   1) Для того чтобы сумма двух натуральных чисел делилась на
   

2, достаточно, чтобы числа были четными.

2. 
   Для того чтобы число делилось на 9,необходимо и достаточно,
   

что бы сумма его цифр делилась на 9.

3. 
   Для того чтобы числа х₁ и х₂ были корнями уравнения х²
   

+рх+q=0,необходимо,что бы х₁ х₂ =q.
Конспект занятия 6 по теме:
61

«Логическая структура математических теорем»
Основная цель: познакомить обучающихся с основными типамилогических структур математических теорем; развивать навыки составления теорем на основе различных логических структур.
Планируемые результаты:
Предметные: знание основных типов логических структурматематических теорем; умение составлять и формулировать прямую теорему, обратную, противоположную, противоположную обратной.
Метапредметные: владение языком математической логики;навыки поиска и выделения необходимой информации; умение выстраивать аргументацию, приводить примеры и контрпримеры; умение строить логические рассуждения и делать обоснованные выводы и умозаключения; навыки планирования и организации учебно-познавательной деятельности; навыки самоконтроля; коммуникативные навыки в ходе комментирования решений и ответов учащихся.
Личностные: ценностное отношение к математическим знаниям;целеустремленность и увлеченность при решении математических задач; способность к логическим умозаключениям; готовность к самообразованию.
Этапы занятия:

1. 
   Постановка цели занятия.
   

2. 
   Теоретическая часть.
   

3. 
   Решение практических заданий.
   

4. 
   Подведение итогов.
   

1. 
   На прошлом занятии, вы узнали, что такое «необходимое и достаточное условие», а так же что такое «условие» и «заключение»
   

теоремы. Сегодня мы рассмотрим различные виды теорем, а так же вы сами попробуете их составить.

2. 
   Теоремы p(x)→ q(х) и q(х)→ p(x) называются взаимно обратными
   

62

теоремами. Иногда одну их них называют прямой,а другую–обратной.
Из определения взаимно обратных теорем следует, что если в формулировке прямой теоремы поменять местами условие и заключение, то получится формулировка обратной теоремы. Например, теорему обратной теореме Пифагора, можно сформулировать так: « Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то этот треугольник прямоугольный».
Как вы думаете, какая теорема называется противоположной? Теоремы
p(x)→ q(х) и p(x q(х) называются взаимно противоположными. Например, для теоремы «Сумма (внутренних) углов треугольника равна
180» противоположной будет теорема, в которой вместо условия и заключения будут сформулированы их отрицания: «У многоугольника, не являющегося треугольников, сумма (внутренних) углов отлична от 180». Обе теоремы верны.
Бывают случаи, когда одна из взаимно противоположных теорем верна,

• 
  другая нет. Например, для теоремы о перпендикулярности диагоналей ромба противоположная ей теорема не верна.
  

Если теорема q(x)→ p(х) обратная для теоремы p(x)→ q(x), q(x p(х) называется противоположной обратной.
Можно показать, что пары теорем: 1) прямая и противоположная обратной; 2) обратная и противоположная – всегда одновременно истинны или ложны.
Убедимся в этом, составив таблицу истинности.
Например, А-условие теоремы, В-заключение теоремы: А→В – прямая
те – – А

– противоположная обратной.

А	В	А	В	А→В	В→А		В
									А
0	0	1	1	1	1	1			1
0	1	1	0	1	0	0			1
							63

1	0	0	1	0	1	1	0
1	1	0	0	1	1	1	1

Например:
Прямая теорема«Биссектрисы внутренних углов треугольникапересекаются в одной точке» истина.
Обратная ей теорема«Если биссектрисы внутренних угловмногоугольника пересекаются в одной точке, то этот многоугольник является треугольником» ложна (например, у ромба, являющегося четырехугольником, биссектрисы внутренних углов пересекаются в одной точке).
Противоположная теорема«Если многоугольник не являетсятреугольником, то биссектрисы его внутренних углов не пересекаются в одной точке» (контрпример – ромб).
Теорема противоположная обратной «Если биссектрисы внутренних углов многоугольника не пересекаются в одной точке, то этот многоугольник не является треугольником», истинна.
Вспомним теорему Виета: Если уравнение x²+px+q=0 имеет корни x₁ и x₂ , то для них выполняются равенства x₁+x₂=-p, x₂· x₂=q.
Как будет звучать обратная теорема Виета?
Если числа x₁ и x₂ таковы, x₁+x₂=-p, x₂· x₂=q, то x₁ и x₂ являются корнями квадратного уравнения x²+px+q=0.

Заметим, что при решении задач на уроках математики используется обратная теорема Виета.
Например, решим следующее уравнение х²-5х+6=0.
Допустим, это уравнение имеет корни, а именно, x₁ и x₂ . Тогда по
обратной теореме Виета одновременно должны выполняться
равенства 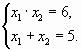. Обратим внимание, что произведение корней – положительное число. А значит, корни уравнения одного знака. А так как сумма корней также является положительным числом, делаем вывод, что оба корня уравнения – положительные. Вернемся снова к произведению корней.
64
Допустим, что корни уравнения – целые положительные числа. Тогда получить верное первое равенство можно только двумя способами (с точностью до порядка множителей): 1·6=6 или 2·3=6. Проверим для предложенных пар чисел выполнимость второго утверждения теоремы Виета: 1+6 ≠ 5, 2+3 =5. Таким образом, числа 2 и 3 удовлетворяют обоим равенствам, а значит, и являются корнями заданного уравнения.
Ответ: 2; 3.

2. 
   Выполним следующие задания:
   

1. 
   Привести контрпример опровергающий утверждение:
   

1. 
   В любой четырехугольник можно вписать окружность;
   

2. 
   Для любого треугольника сумма квадратов двух его сторон равна квадрату третьей стороны;
   

3. 
   Сумма чисел с разными знаками есть число отрицательное;
   

4. 
   В равнобедренном треугольнике один угол тупой.
   

2.Сформулируйте обратную теорему, противоположную теорему и теорему противоположную обратной для данных теорем. Установите истинность каждой.

1. 
   Угол называется развернутым, если обе его стороны лежат на одной прямой.
   

2. 
   Если суммы противолежащих углов четырехугольника равны по 180°, то около четырехугольника можно описать окружность.
   

3. 
   Если две параллельные прямые пересечены секущей, то образовавшиеся накрест лежащие углы равны.
   

Ответы:

1. 
   1) В прямоугольную трапецию или в ромб нельзя вписать окружность;
   

2) Например, треугольник со сторонами 2,3 и 4 (2²+3² ≠ 4²) или равносторонний треугольник;
3) Например, -2+3+4= 5, 5 – число положительное;
65

4. 
   Равнобедренный треугольник с углами при основании 45
   

градусов (два угла острых, один прямой);

2. 
   1) А – угол развернутый, В – обе стороны лежат на одной прямой.
   

Прямая: «Угол называется развернутым,если обе его стороны лежатна одной прямой» - истинна.
Обратная: «Если обе стороны угла лежат на одной прямой,то уголназывается развернутым» - истинна.
Противоположная: «Угол не является развернутым,если обе егостороны не лежат на одной прямой» - истинна.
Противоположная обратной: «Если обе стороны угла не лежат наодной, то угол не является развернутым» - истинна.

2. 
   А – сумма противолежащих углов равна 180°, В – описать окружность.
   

Прямая: «Если суммы противолежащих углов четырехугольника равныпо 180°, то около четырехугольника можно описать окружность» – истинна.
Обратная: «Сумма противолежащих углов четырехугольника,вписанного в окружность, равна 180°» - истинна.
Противоположная: «Если суммы противолежащих угловчетырехугольника не равны 180°, то около четырехугольника нельзя описать окружность» - истина .
Противоположная обратной: «Если около четырехугольника нельзяописать окружность, то сумма его противолежащих углов не равна 180°» - истина.

3. 
   А – две параллельные прямые пересечены секущей, В – накрест лежащие углы равны.
   

Прямая: «Если две параллельные прямые пересечены секущей,тообразовавшиеся накрест лежащие углы равны» - истинна.
Обратная: «Если при пересечении двух прямых секущей,образовавшиеся накрест лежащие углы равны, то эти прямые параллельны» - истинна.

66

Противоположная: «Если две не параллельные прямые пересеченысекущей, то образовавшиеся накрест лежащие углы не равны» - истина.
Противоположная обратной: «Если при пересечении двух прямыхсекущей, образовавшиеся накрест лежащие углы не равны, то эти прямые не параллельны» - истина.