диплом. Программа курса по выбору Математическая логика для школьников
 Скачать 0.8 Mb. Скачать 0.8 Mb.
|
|
2.3. Педагогический эксперимент: основные этапы и результаты Для установления уровня сформированности основ математической компетентности в области «Математическая логика» у обучающихся 9 классов на базе МБОУ СОШ №150 г. Красноярска был проведен констатирующий этап эксперимента. эксперименте приняли участие учащиеся 9 класса в количестве 20 человек. Для выявления уровня сформированности основ математической компетентности в области «Математическая логика» мы выделили следующие компоненты: - когнитивный (система знаний, которая необходима для решений актуальных задач учебной деятельности, а так же определяет уровень интеллектуального развития); - праксиологический (совокупность умений, навыков и способов деятельности обучающихся, и их применении в собственной учебной деятельности); - аксиологический (осознание обучающимися ценности и значимости математики как науки) На основе выделенных компонентов, а также для аналитической обработки результатов исследования и получения количественных показателей условно были выделены три уровня сформированности математической компетентности в области «Математическая логика»: низкий, средний и высокий. Низкий уровень (пороговый) – знание базовых понятий, методов и правил, которые необходимы для решения задач. Умение применять знания при решении элементарных задач в одно действие. Понимание необходимости изучения математической логики, но при этом отсутствие проявление интереса к логическим задачам. Средний уровень (базовый) – знание базовых понятий, методов и правил, которые необходимы для решений задач. Решение типовых задач. 80 Умения применять методы решения логических задач. Понимание важности изучения математической логики, освоения способов и методов решения, проявление интереса к логическим задачам. Высокий уровень (продвинутый) – знание понятий, методов и правил, которые необходимы для решения задач. Умение размышлять, строить самостоятельно алгоритм действий, уметь объяснять решение задачи. Понимание важности математической логики, освоение разнообразных способов действий. Для выявления уровня сформированности математической компетентности в области «Математическая логика» учащимся было предложено три среза. Срез 1 Если условие А: х>1; условие В: x>10; условие С: x>13; условие D: x>20, то а) С необходимо для А; б) С необходимо для В; в) D необходимо для А; г) В необходимо для С; д) D необходимо для В Если условие А: x<0; условие В: x<2; условие С: x<20; условие D: x<30, то а) С достаточно для А; б) В достаточно для D; в) В достаточно для А; г) D достаточно для С; д) D достаточно для А. Утверждение «Если на небе тучи, то идет дождь» имеет логическую структуру: C→D. Определите структуру и установите соответствие для следующих утверждений: 81
На небе есть тучи тогда и только тогда, когда идет дождь. Если х=7, то следующее высказывание истинно: а) х>0 и х=0; б) х>0 или х=0; в) неверно, что х<10; г) x<10 и х>8; д) x>7 и х=7. Определите, какие, из следующих суждений истинны: А) Все Митины одноклассники занимаются спортом. Значит, все спортсмены учатся в Митином классе. Б) Никто из Митиного класса не играет в теннис. Значит, никто из теннисистов не учится в Митином классе. В) Все числа, кратные 8, делятся на 4.Следовательно, все числа, делящиеся на 4, кратны 8. Г) Все параллельные прямые - не пересекаются. Значит, две непересекающиеся прямые - параллельны. Срез 2 Задача 1. Решите следующую задачу и объясните решение. Я отпил 1/6 чашечки черного кофе и долил еѐ молоком. Затем выпил 1/3 чашечки и снова долил еѐ молоком. Потом я выпил пол чашечки и опять долил ее молоком. Наконец, я выпил полную чашечку. Чего я выпил больше – кофе или молока? Задача 2. Решите следующую задачу и объясните решение. На международную конференцию приехали 10 делегатов, не понимающих языка друг друга. Какое минимальное число переводчиков 82 потребуется для обслуживания конференции при условии, что каждый переводчик знает только два языка? Задача 3. Решите следующую задачу и запишите ответ. Ехали два крестьянина, и нашли три бочонка: один восьмиведѐрный с квасом и два пустых – пятиведѐрный и трехведѐрный. Крестьяне решили поделить квас поровну тут же на месте с помощью этих трех бочонков. Как они разделили квас? Срез 3 Согласны ли вы с утверждением: «Математику уже за тем учить следует, что она ум в порядок приводит»? А) нет; Б) скорее нет, чем да; В) скорее да, чем нет; Г) да. Имеете ли вы опыт решения логических задач? А) нет; Б) скорее нет, чем да; В) скорее да, чем нет; Г) да. Хотели бы вы познакомиться с различными методами решения логических задач? А) нет; Б) скорее нет, чем да; В) скорее да, чем нет; Г) да. Как вы считаете, необходимо ли всем изучать математическую логику в школе? А) нет; Б) скорее нет, чем да; В) скорее да, чем нет; Г) да. Используете ли вы законы логических умозаключений в повседневной жизни? А) нет; Б) скорее нет, чем да; В) скорее да, чем нет; Г) да. Первый срез предполагает проверку когнитивного компонента, он включает в себя тестирование. Каждый правильный ответ оценивался в 5 баллов. Второй срез – праксиологический компонент, включает в себя 3 логические задачи разного уровня. Каждая решенная задача оценивалась в 5 баллов. Третий срез – аксиологический компонент. В этом срезе учащимся нужно было ответить на вопросы анкеты. Ответ «нет» оценивался в 2 балла, «скорее нет, чем да» - 3 балла, «скорее да, чем нет» - 4 балла, «да» - 5 баллов. 83 Результаты констатирующего этапа педагогического эксперимента приведены в следующей таблице 1: Таблица 1 Результаты констатирующего этапа педагогического эксперимента
Обработка полученных данных Если сумма баллов 50-65(max) , можно считать, что уровень сформированности основ математической компетентности в области «Математическая логика» высокий, если 35-49 баллов, то средний уровень, если менее 35,то низкий уровень. На рис.1 представлена диаграмма уровня сформированности основ математической компетентности у обучающихся в области «Математическая логика» на констатирующем этапе педагогического эксперимента. 84     класс класс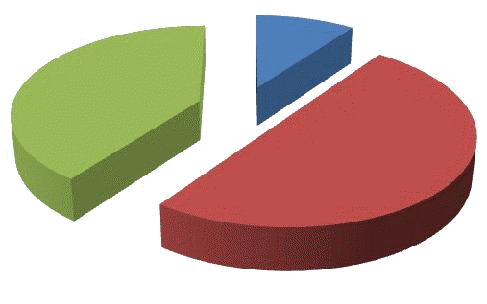  10% 40% 50% Высокий Средний Низкий Рис 1. Диаграмма уровня сформированности основ математической компетентности у учащихся 9 класса в области «Математическая логика» на констатирующем этапе эксперимента. Результаты констатирующего этапа педагогического эксперимента показали, что у 40% учащихся 9 класса (ученики, которые набрали менее 35 баллов) низкий уровень сформированности основ математической компетентности в области «Математическая логика». У 10% принявших участие в эксперименте учащихся высокий уровень сформированности основ математической компетентности. У 50% учащихся – средний уровень сформированности математической компетентности. Основываясь на результатах диагностики, можно сделать вывод о необходимости формирования у большинства учащихся 9 класса основ математической компетентности в области «Математическая логика». рамках формирующего этапа эксперимента на базе школы №150 города Красноярска, нами было организовано обучение учащихся 9 классов курсу по выбору «Математическая логика для школьников». В ходе педагогической практики было проведено 7 занятий по 2 часа в неделю. По наблюдениям, отметим следующее, что обучающиеся были активны на занятиях, ученикам очень понравились разные способы решения логических задач, а именно метод графов и метод таблиц, с помощью них они с легкостью решали задачи. Во время изучения курса ученики проявляли 85 интерес к изучаемому материалу, задавали вопросы, проводили между собой дискуссии. После целенаправленной работы по повышению уровня сформированности основ математической компетентности в области «Математическая логика», был проведен завершающий этап педагогического эксперимента, с целью выявления динамики уровня сформированности основ математической компетентности в области «Математическая логика» у учащихся 9 класса. Учащимся было предложено три среза. Срез 1 Если условие А: х>3; условие В: x>16; условие С: x>22; условие D: x>19, то а) С необходимо для А; б) С необходимо для В; в) D необходимо для А; г) В необходимо для С; д) D необходимо для В Если условие А: x<2; условие В: x<6; условие С: x<24; условие D: x<30, то а) С достаточно для А; б) В достаточно для D; в) В достаточно для А; г) D достаточно для С; д) D достаточно для А. Утверждение «Если на небе солнце, то на улице день» имеет логическую структуру: А→В. Определите структуру и установите соответствие для следующих утверждений:
86 3) Если на улице не день, то на небе нет Г) ¬А→¬В солнца; На небе есть солнце тогда и только тогда, когда на улице день. 4.Если х=9, то следующее высказывание истинно: а) х>0 и х=0; б) х>0 или х=0; в) неверно, что х<10; г) x<10 и х>8; д) x>9 и х=9. Определите, какие, из следующих суждений истинны: А) Каждая планета Солнечной системы вращается вокруг своей оси. Б) Если 12 делится на 6, то оно делится на 3. В) Для того, чтобы четырѐхугольник был квадратом, достаточно, чтобы его диагонали были равны и перпендикулярны. Г) Найдется целое число х удовлетворяющее соотношению х2=0. Срез 2 Задача 1. Решите следующую задачу и объясните решение. Две стрелки насажены на одну ось и в некоторый момент времени совмещены. Одна из стрелок описывает круг за 12 часов, а друга за 16 часов. Через какое время стрелки совместятся опять? Задача 2. Решите следующую задачу и объясните решение. Из ведра, содержащего 5 литров воды, отливают 1 литр, а затем в ведро вливают 1 литр сока. Перемешав все это, из ведра отливают 1 литр смеси, затем в ведро опять вливают 1 литр сока. Опять перемешивают, отливают 1 литр смеси и вливают 1 литр сока. Сколько в ведре после этого останется воды? Задача 3. Решите следующую задачу и запишите ответ. Двое, Андрей и Федор, обмениваются деньгами. Сначала Андрей отдал часть своих денег Федору, потом Федор Андрею, затем опять Андрей Федору и наконец, Федор отдал Андрею деньги в последний раз, и после 87 этой передачи у каждого стало по 160 рублей. Количество передаваемых денег всякий раз было равно количеству у получающего их. Сколько денег было у Андрея и Федора первоначально? Срез 3 Согласны ли вы с утверждением: «Математику уже за тем учить следует, что она ум в порядок приводит»? А) нет; Б) скорее нет, чем да; В) скорее да, чем нет; Г) да. Имеете ли вы опыт решения логических задач? А) нет; Б) скорее нет, чем да; В) скорее да, чем нет; Г) да. Хотели бы вы познакомиться с различными методами решения логических задач? А) нет; Б) скорее нет, чем да; В) скорее да, чем нет; Г) да. Как вы считаете, необходимо ли всем изучать математическую логику в школе? А) нет; Б) скорее нет, чем да; В) скорее да, чем нет; Г) да. Используете ли вы законы логических умозаключений в повседневной жизни? А) нет; Б) скорее нет, чем да; В) скорее да, чем нет; Г) да. Результаты завершающего эксперимента приведем в следующей таблице 2: Таблица 2 Результаты завершающего этапа педагогического эксперимента
88
Анализ срезов показал некоторое повышение у учащихся уровня сформированности основ математической компетентности в области «Математическая логика». Улучшилось качество выполнения заданий, для решения которых, обучающиеся использовали знания, полученные в ходе изучения курса по выбору «Математическая логика для школьников». На рис.2 представлена диаграмма уровня сформированности основ математической компетентности у обучающихся 9 классов в области «Математическая логика» на завершающем этапе педагогического эксперимента.     | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
