диплом. Программа курса по выбору Математическая логика для школьников

• Название: Программа курса по выбору Математическая логика для школьников
• Анкор: диплом
• Дата: 15.02.2021
• Размер: 0.8 Mb.
• Имя файла: диплом.docx
• Тип: Программа курса; #176550
• страница: 10 из 10

класс


5%
50%

Высокий

45%

Средний
Низкий


Рис 2. Диаграмма уровня сформированности основ математической
компетентности в области «Математическая логика» на завершающем этапе
эксперимента.
На рис. 3 представлена динамика сформированности основ
математической компетентности в области «Математическая логика» у
учащихся 9 класса.
89

60%		50%				50%
50%							45%
											40%
40%
30%
20%
		10%
10%											5%
0%
			Высокий				Средний					Низкий
				в начале эксперимента					в конце эксперимента

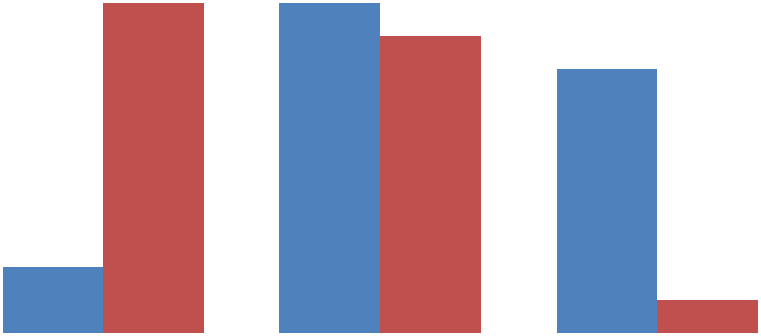Рис 3. Динамика сформированности основ математической компетентности в области «Математическая логика» у учащихся 9 класса.
Сравнивая результаты проведенных экспериментов –
констатирующего и завершающего – можно сделать вывод, что разработанный нами курс по выбору «Математическая логика для школьников» позволяет повысить уровень сформированности основ математической компетентности в области «Математическая логика».
Результаты эксперимента и наблюдений позволяют сказать, что после изучения курса по выбору «Математическая логика для школьников», учащиеся не только научились использовать элементы математической логики и различные методы решения логических задач, но и стали более уверенными при аргументировании своих мыслей, значительно повысился познавательный интерес к вопросам математической логики.


90
Заключение

• 
  ходе проведенного исследования, проанализировав литературу, опыт учителей и результаты диагностики мы пришли к выводу: что необходимо формировать у учащихся основы математической компетентности в области «Математическая логика».
  

Под математической компетенцией мы понимаем способность структурировать данные (ситуацию), выделять математические отношения,
создавать математическую модель ситуации, анализировать и преобразовывать ее, интерпретировать полученные результаты.
Для удобства диагностики уровня сформированности основ математической компетентности у учащихся в области «Математическая логика» условно выделили три уровня сформированности математической компетентности: низкий, средний, высокий.
Нами был разработан курс по выбору для обучающихся 9 классов «Математическая логика для школьников», рассчитанный на 16 часов (2 часа

• 
  неделю).
  

На базе школы №150 города Красноярска, были проведены диагностирующий, формирующий и констатирующий этапы эксперимента. Результаты констатирующего этапа эксперимента свидетельствую о повышении уровня математической компетентности в области «Математическая логика» после изучения курса по выбору «Математическая логика для школьников».
Можно сделать вывод, что разработанный нами курс по выбору «Математическая логика для школьников» способствует повышению уровня сформированности основ математической компетентности в области «Математическая логика» у обучающихся 9 классов в процессе предпрофильного обучения математике.


91

Список используемой литературы

1. 
   Алимов Ш.А. Алгебра. 9 класс. 17-е изд. - М.: 2012. - 287 с.
   

2. 
   Богомолова О.Б. Логические задачи. 4-е изд., испр. и доп. – М. : БИНОМ. Лаборатория знаний, 2013. – 277с. :ил.
   

3. 
   Болотов В.А., Сериков В.В. Компетентностная модель: от идеи к образовательной программе // Педагогика. 2003. №10. С. 8–14.
   

4. 
   Виленкин Н.Я., Жохов В.И. и др. Математика.5 класс. 31-е изд.,стер. - М: 2013. - 280с.
   

5. 
   Виленкин Н.Я., Сурвилло Г.С. и др. Алгебра. 9 класс. С углубленным изучением математики. 7-е изд. - М.: 2006. - 368 с.
   

6. 
   Голунова А.А. Обучение математике в профильных классах: учеб. -метод. пособие / А.А. Голунова. – 2-е изд., стер. – М .: ФЛИНТА,
   

2014. – 204 С.

7. 
   Гончарова О. С. Развитие логического мышления на уроках математики в начальных классах // Молодой ученый. — 2012. — №10. — С.
   

329-331.

8. 
   Делор Ж. Образование: сокрытое сокровище // Основные положения Доклада Международной комиссии по образованию XXI века. М.:
   

9. 
   Дорофеев Г.В., Петерсон Л.Г. Математика. 5 класс. 2-е изд., перераб. - М.: 2011; Ч.1 - 176с, Ч.2 - 240с.
   

9. 
   Дорофеев Г.В., Петерсон Л.Г. Математика. 5 класс. 2-е изд.,
   

перераб. - М.: 2010; Ч.1 - 1112с, Ч.2 - 128с., Ч.3 - 176с.
11. Елифантьева С.С. Технология изучения элементов математической логики в основной школе: Дис… канд. пед. наук. ЯГПУ им. К.Д. Ушинского, Ярославль, 2006.
12. Жуковская Е.П. Дидактические аспекты организации
факультативов [Электронный ресурс].- Режим доступа:
http://festival.1september.ru. – (Дата обращения: 4.02.17).
92

13. 
    Зарипова Р.М. Формирование ключевых компетенций у школьников на уроках математики.//Практика и тенденции социального партнерства в системе школа – СПО - ВУЗ: материалы VI Республиканской научно-методической конференции: в 2 ч. Ч. II; М-во образ. и науки России, Казан. нац. исслед. технол. ун-т. – Казань, 2013 г. - С.175-178.
    

13. 
    Зарукина Е. В. Активные методы обучения: рекомендации по разработке и применению: учеб.-метод. пособие / Е. В. Зарукина, Н. А. Ло-
    

гинова, М. М. Новик. СПб.: СПбГИЭУ, 2010. – 59 с.

15. 
    Зимняя И.А. Ключевые компетенции – новая парадигма результата образования // Высшее образование сегодня. 2003. № 5. С. 34–42.
    

15. 
    Кейв М.А., Власова Н.В. Инновационные процессы в профильном образовании: учебное пособие; Краснояр. гос. пед. ун-т им В.П. Астафьева. – Красноярск, 2015. – 168с.
    

15. 
    Коджаспирова Г.М., Коджаспиров А.Ю. Педагогический словарь: Для студ. высш. и сред. пед. учеб. заведений. — М.: Издательский центр «Академия», 2003. — 176 с.
    

15. 
    Козлова С.А.. Математика. 5 кл.: учеб. для организации, осуществляющих образовательную деятельность. В 2 ч./ Козлова С.А., Рубин А.Г. –Изд. 2-е. – М.: Баласс, 2015. – 208 с.: ил. ( Образовательная система «Школа 2100»).
    

15. 
    Козлова С.А.. Математика. 6 кл.: учеб. для общеобразоват. учреждений.: в 2-х частях./ Козлова С.А., Рубин А.Г. –Изд. 2-е. – М.: Баласс,
    

2013. – 208 с.: ил. ( Образовательная система «Школа 2100»).
20. Лысогорова Л.В. Педагогически условия развития математических способностей младших школьников [Текст]./ Лысогорова Л.В. // Сибирский педагогический журнал. -2007.-№9.- С.228-233.

21. 
    Муравин Г.К, Муравина О.В. Математика. 5 класс. 3-е изд., стер.
    

• 
  М.: 2014. - 320с.
  

22. 
    Муравин Г.К, Муравина О.В. Математика. 6 класс. 2-е изд., стер.
    

• 
  М.: 2014. - 320 с.
  

93

23. 
    Ожегов, С.И. Словарь русского языка: ок. 53000 слов / С.И. Ожегов; под общ. ред проф. Л.И. Скворцова. – 24-е изд., испр. – М.: ООО
    

«Издательство Оникс»: ООО «Издательство Мир и образование», 2007. – 640
с.
24. Основные результаты международного исследования образовательных достижений учащихся PISA-2006 [Электронный ресурс]: Центр оценки качества образования ИСМО РАО. Руководитель работы -
Ковалева Г.С.- URL:
http://window.edu.ru/catalog/pdf2txt/351/60351/30272?p_page=10 (Дата обращения: 27.02.16)

25. 
    Платонова Е.Н., Буслова Н.С. Организация факультативного курса «путешествие в историю информатики» для учащихся школы: материалы VI Международной студенческой электронной научной конференции "Студенческий научный форум 2014": Тобольская гос. соц.-
    

пед. ак. им. Д.И.Менделеева.- Тобольск, 2014.

26. 
    Предпрофильная подготовка учащихся: Разработка и экспертиза курсов по выбору. Структура и содержание портфолио (методические рекомендации). – Вологда: Издательский центр ВИРО, 2006. – 84 с.
    

26. 
    Примерная основная образовательная программа основного общего образования: одобрена решением федерального учебно-
    

методического объединения по общему образованию (протокол от 8 апреля 2015 г. №1/15)

28. 
    Тойбекова Б.А., Торыбаева Ж.З. Особенности организации факультативных занятий в контексте приобщения учащихся к полиязычию:
    

материалы международной научно-практической конференции «Гуманитарные и естественные науки в стратегическом развитии современного образовательного учреждения»: Институт мировой экономики

• 
  финансов.- Астрахань, 2016.
  

29. 
    Тумашева О.В., Берсенева О.В. Комплексное методическое
    

портфолио как средство мониторинга формирования методических
94

компетенций будущих учителей математики // Интернет-журнал
«НАУКОВЕДЕНИЕ» Том 7, №5 (2015) http://naukovedenie.ru/PDF/06PVN515.pdf (доступ свободный). Загл. с экрана. Яз. рус., англ. DOI: 10.15862/06PVN515
30. Федеральный государственный образовательный стандарт основного общего образования (утвержден приказом Минобрнауки России от 17 декабря 2010 г. № 1897)

31. 
    Хуторской А.B. Ключевые компетенции как компонент личностно-ориентированного образования // Народное образование. – 2003. -
    

№2. – С.58-64.

32. 
    Хуторской А.В. Ключевые компетенции как компонент личностно-ориентированной парадигмы образования // Ученик в обновляющейся школе. Сборник научных трудов.— М.: ИОСО РАО, 2002. –
    

• 
  135-157.
  

33. 
    Шкерина JI.B., Багачук А.В., Кейв М.А., Шашкина М.Б. Теоретические основы и технологии измерения и оценивания профессиональных компетенций студентов – будущих учителей математики: монография. Краснояр. гос. пед. ун-т им. В.П. Астафьева. Красноярск, 2013.-
    

280с.
34. Штеймарк О.В. Педагогические условия эффективного использования компьютерных технологий в педагогическом процессе. // Научный потенциал: работы молодых ученых. – 2008.-№1.- С.211-215.


95