матан. заочники матем 1 семестр по вариантам. Программа, методические указания и контрольные задания 1 семестра для студентов заочной формы обучения всех специальностей

• Название: Программа, методические указания и контрольные задания 1 семестра для студентов заочной формы обучения всех специальностей
• Анкор: матан
• Дата: 22.01.2021
• Размер: 374.69 Kb.
• Имя файла: заочники матем 1 семестр по вариантам.docx
• Тип: Программа; #170540
• страница: 21 из 23

Вариант 8

Задание 1.1. Решить матричное уравнение:

_ 2 1 1 _{ } 1 1 2 _

X  ^ 1 1 1 ^  ^ 6 2 3 ^.

   

^ 2 1 2 ^{ } 1 0 0 ^

   

Задание 1.2. Решить системы линейных уравнений:

_x  2 y  z  2;


а) ^2x  3y  2z  2;



^3x  y  z  8

_x  3y  2z  6;



б) ^x  2 y  z  3;



^2x 5 y 3z 9

методом Крамера;


методом Гаусса (если система имеет бесконечное

множество решений, то найти общее решение через свободную переменную z и частное решение при z = 1).

Задание 2.1. Даны координаты трех точек: А (11, 2), В (4, 5), С (–2, 9).

а) Найти уравнение прямой АН, перпендикулярной прямой ВС в общем, каноническом и параметрическом виде.

б) Определить взаимное расположение векторов AO и BC , где О – середина ВС.

Задание 2.2. Привести уравнения второго порядка к каноническому виду.

Определить тип кривой, которое оно задает. Построить кривую.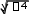

а) x² 12x y² 10 y 60  0; б)  4x 6.
Задание 2.3. Даны координаты четырех точек:

A (2, 3, –1), B (4, 3, 1), C (0, 2, –1), D (3, 5, –3).

а) Написать уравнение плоскости АВС; б) Найти площадь треугольника АВС;

в) Найти двумя способами длину высоты, опущенной из вершины D тетраэдра АВСD на грань АВС (используя формулы векторной алгебры и формулу расстояния от точки до прямой).

Задание 3.1. Вычислить пределы:

x²  5

а) ^lim (отношение степенных функций);

x

б) lim

9x⁴  3 1

tg_x²  4x_



2

(использование первого замечательного предела или

x0

x  x

использование эквивалентных функций);

x1

в) lim

_ x  4 _ 2

 



(использование второго замечательного предела).

^x _ x  2 _

Задание 3.2. Найти производные:

а) y  ² x 



_ cos(1  2x) _{ e3;}


б) y  x^{1 x}.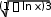

3 1  cos(2x)

Задание 3.3. Вычислить предел, используя правило Лопиталя:

lim tg x ln x.

x00

Задание 3.4. Провести полное исследование функции с помощью производных первого и второго порядков. По результатам исследования построить графики:

а) y  ^{3x  2} ;

_x2

б) y  (x 1)  e^x.

Задание 4.1. Найти экстремум функции двух переменных

z  6xy  4x³  2 y² 1 или доказать, что его не существует.

Задание 4.2. Найти наибольшее и наименьшее значения функции

z x²  y²  xy 6y 3x

в области

D : 0  x 1, 0  y  3.