матан. заочники матем 1 семестр по вариантам. Программа, методические указания и контрольные задания 1 семестра для студентов заочной формы обучения всех специальностей

• Название: Программа, методические указания и контрольные задания 1 семестра для студентов заочной формы обучения всех специальностей
• Анкор: матан
• Дата: 22.01.2021
• Размер: 374.69 Kb.
• Имя файла: заочники матем 1 семестр по вариантам.docx
• Тип: Программа; #170540
• страница: 23 из 23

Вариант 10

Задание 1.1. Решить матричное уравнение:

_ 1 0 1 _{ } 1 2 1_

X  ^ 2 1 0 ^  ^ 2 1 3^.

   

^ 1 1

_2  

2 4 3^

   

Задание 1.2. Решить системы линейных уравнений:



_2x  4 y  z  4;

а) _3x  6 y  2z 4;



^4x  y  3z  1

_x  y  3z  1;

методом Крамера;


б) ^x  3y  z  7; методом Гаусса (если система имеет бесконечное



^3x  y  5z 5
множество решений, то найти общее решение через свободную переменную z и частное решение при z = 1).

Задание 2.1. Даны координаты трех точек: А (5, –3), В (7, 2), С (9, 8).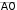

а) Найти уравнение прямой АН, перпендикулярной прямой ВС в общем, каноническом и параметрическом виде.

б) Определить взаимное расположение векторов середина ВС.

и BC , где О–

Задание 2.2. Привести уравнения второго порядка к каноническому виду.

Определить тип кривой, которое оно задает. Построить кривую.

а) 3y² 12 y 2x²  8x 3  0;

б) x  2 

1 3y.

Задание 2.3. Даны координаты четырех точек:

A (5, 3, 2), B (–1, 3, 4), C (0, 2, –1), D (3, 5, –2).

а) Написать уравнение плоскости АВС; б) Найти площадь треугольника АВС;

в) Найти двумя способами длину высоты, опущенной из вершины D тетраэдра АВСD на грань АВС (используя формулы векторной алгебры и формулу расстояния от точки до прямой).

Задание 3.1. Вычислить пределы:

а) lim

x0

(отношение степенных функций);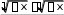

4x

б) lim

x0

tg(3x   3)  sin(2x) arcsin x²
(использование первого замечательного

предела или использование эквивалентных функций);

_{ x 1 }12x

в) lim _{ } (использование второго замечательного предела).

^x _ x _

Задание 3.2. Найти производные:

а) y 

cos x

• 
  x ln^ tg ^x  2^e;
  

б) y ^ex

_{2  2 } x .

sin x  

Задание 3.3. Вычислить предел, используя правило Лопиталя:

lim ^x .



x _ln² _x

Задание 3.4. Провести полное исследование функции с помощью производных первого и второго порядков. По результатам исследования построить графики: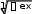

_x2

а) y 

3  x^;

б) y .

Задание 4.1. Найти экстремум функции двух переменных

z 4x²  y²  24x 2 y17

или доказать, что его не существует.

Задание 4.2. Найти наибольшее и наименьшее значения функции

z  5x²  y²  3xy  2 в области

D : x  1, y  1, x  y 1.

Литература

1. 
   Берман Г.Н. Сборник задач по курсу математического анализа / Г.Н. Берман. М.: Наука, 2002. - 443 с.
   
2. 
   Бронштейн И.Н. Справочник по математике для инженеров и учащихся втузов / И.Н. Бронштейн, К.А. Семендяев. М.: Наука, 1980. - 946 с.
   
3. 
   Данко П.Е.Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова.М.: Высшая школа, 1997. Ч. 1, 2. - 304 с.
   
4. 
   Демидович Б.П. Краткий курс высшей математики / Б.П. Демидович. М.: Изд-во «Астрель», 2003. - 654 с.
   
5. 
   Краснов М.Л. Вся высшая математика / М.Л. Краснов, А.И. Киселев, Г.И. Макаренко. М.: Эдиториал УРСС, 2001. Ч. 1. - 352 с.
   
6. 
   Линейная алгебра и основы математического анализа: сб. задач по математике для втузов / под ред. А.В. Ефимова и Б.П. Демидовича. М.: Наука, 1996. - 464 с.
   
7. 
   Минькова Р.М. Векторная алгебра и аналитическая геометрия / Р.М. Минькова. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2005. - 41 с.
   
8. 
   Минькова Р.М. Дифференциальное исчисление функции одной переменной / Р.М. Минькова. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2005. - 57 с.
   
9. 
   Минькова Р.М. Дифференциальное и интегральное исчисление функции нескольких переменных / Р.М. Минькова. Екатеринбург: ГОУ ВПО УГТУ- УПИ, 2005. - 70 с.
   
10. 
    Минькова Р.М. Элементы линейной алгебры / Р.М. Минькова. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2005. - 46 с.
    
11. 
    Натансон И.П. Краткий курс высшей математики / И.П. Натансон. СПб.: Изд-во «Лань», 2003. - 736 с.
    
12. 
    Письменный Д.Т. Конспект лекций по высшей математике / Д.Т. Письменный. М.: Айрис-пресс, 2003. Ч.1, 2. - 288 с.
    

Приложение

Образец титульного листа

ФГАОУ ВО «Уральский Федеральный Университет имени первого Президента России Б.Н. Ельцина»

Институт радиоэлектроники и информационных технологий – РТФ Департамент информационных технологий и автоматики


Контрольная работа № 1 по математике
Вариант № 0
студент Иванов И.И.

институт ИРИТ-РтФ

группа РИЗ-170000

зачетная книжка № 00000000

1.1	1.2.		2.1.		2.2.			2.3.
	а	б	а	б		а	б		а	б	в

3.1.			3.2.		3.3.		3.4.			4.1.		4.2.
а	б	в	а	б			а	б

Екатеринбург 2017