матан. заочники матем 1 семестр по вариантам. Программа, методические указания и контрольные задания 1 семестра для студентов заочной формы обучения всех специальностей
 Скачать 374.69 Kb. Скачать 374.69 Kb.
|
Задание 2.3.Даны координаты четырех точек: (x 3)2 6( y 2), где x 3. А(4,1,3), B(0,2,1), C(1,3,2), D(2,2, 5). а) Написать уравнение плоскости АВС; б) Найти площадь треугольника АВС; в) Найти двумя способами длину высоты, опущенной из вершины D тетраэдра АВСD на грань АВС (используя формулы векторной алгебры и формулу расстояния от точки до прямой). Решение. а) Для того чтобы написать уравнение плоскости нужна произвольная точка на этой плоскости и два вектора, параллельные плоскости.  4 Каноническое уравнение параболы имеет вид (x x0 )2 2 p( y y0 ) или ( y y0 )2 2 p(x x0 ) 5 Для более точного построения можно найти дополнительную точку. В частности, при х = 6 получаем, что у = 0,5; т. е. ветвь параболы проходит через точку (6; 0,5). АВС : A(4,1,3), AB {4,1, 2}, AC {5,2, 1}. x 4 4 y 1 1 z 3 2 x 4 1 2 y1 4 2 z 3 4 1 5 2 1 2 1 5 1 5 2 3 x 4 6 y 1 3 z 3 3x 6 y 3z 9 0. АВС : x 2y z 3 0. Ответ. АВС: x 2y z 3 0. векторного произведения: SABC [ AB, AC] . 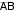 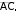 Площадь ΔABC, построенного на векторах и длины их векторного произведения Площадь ΔABC, построенного на векторах и длины их векторного произведения Вычисляем векторное произведение: равна половине 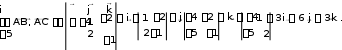 Найдем длину полученного вектора:   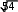  3 6. 3 6.Тогда SABC 1 AB, AC 3 6 . 2  2 Ответ. 3 6 S . 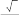 ABC 2 ABC 2 в) Двумя способами найти длину высоты, опущенной из вершины D тетраэдра АВСD на грань АВС. способ: через приложение смешанного произведения векторов к вычислению объема тетраэдра. 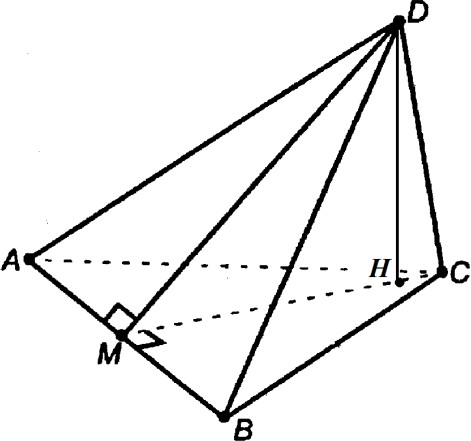 Рисунок 4. Высота тетраэдра  6  Объем тетраэдра, с одной стороны, равен одной шестой модуля смешанного произведения трех векторов, на которых он построен: Объем тетраэдра, с одной стороны, равен одной шестой модуля смешанного произведения трех векторов, на которых он построен: VABCD 1 AB, AC, AD . С другой стороны, V ABCD 1 S 3 ABC DH, отсюда DH 3VABCD . 
 SABC SABC Получим, что DH AB, AC, AD 4 1 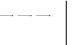 5 2 5 22 1 2  1 24. 1 24.8 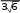 DH DH 24 8 4 6 . 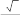 3 3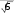 способ: применить формулу расстояния от точки до плоскости. способ: применить формулу расстояния от точки до плоскости.Длина высоты тетраэдра равна расстоянию от точки плоскости ABC Расстояние от точки до плоскости можно найти по формуле: D(2,2, 5) 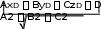 d (D, ABC) . d (D, ABC) .Числитель получается, если в левую часть уравнения плоскости ABC подставить координаты точки D В знаменателе находится длина нормального вектора плоскости ABC (координаты нормального вектора плоскости – коэффициенты перед неизвестными в ее уравнении). Получим: DH d (D, ABC) 8 4 6 . 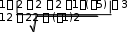 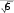  3 3Ответ. DH 4 6 .  3 3 | ||||||