матан. заочники матем 1 семестр по вариантам. Программа, методические указания и контрольные задания 1 семестра для студентов заочной формы обучения всех специальностей
 Скачать 374.69 Kb. Скачать 374.69 Kb.
|
Задание 3.2.Найти производные функций:  x3 4 x3 4sin x 4 e x ln x  а) y x2 1 3 ln(1 x ) ; б) y x 1 . Решение. а) Для нахождения производной первой функции используем правила дифференцирования и таблицу производных элементарных функций. Данную функцию представим в виде суммы трех функций и вычислим производную каждого слагаемого: y y1 y2 y3.  x3 4 x3 4 y 1 x2 1 [используем правила дифференцирования частного u uv uv , суммы и разности функций u v u vи правило v v2 дифференцирования сложной функции: если y y(u), u u(x), то yx yu ux] =   x3 4 x2 1 x3 4 x2 1  x2 1 x2 1x3 4 x2 1 2  2 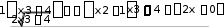 x2 1 x2 1 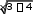 2  x2 1 x2 1 3x2 x2 1 4x x3 4 3x4 3x2 4x4 16x x4 3x2 16x   2 ; 2 ; 2 x3 4 x2 1 2 x3 4 x2 12 y 3sin x ln1 x4 [используем правила дифференцирования произведения u v u v u v , разности функций и правило дифференцирования сложной функции] = = 3sin x ln1 x4 3sin x ln1 x4 3sin x ln 3sin x ln 1 x4 3sin x1 1 x4 1 x4 3sin x ln 3 cos x ln1 x 4 3sin x 4x3  4 4 3sin x ln 3 cos x ln 1 x4 4x3  4 ; 4 ; 1 x x1 y3 e 0 нулю]. [функция является константой, поэтому ее производная равна y y1 y2 y3 x4 3x2 16x 3sin x ln 3 cos x ln1 x4 4x3 .  x4 1  Ответ.  y y x4 3x2 16x 3sin x ln 3 cos x ln1 x4 4x3 .  x4 1 б) Для нахождения производной второй функции используем правило логарифмического дифференцирования. Логарифмируя обе части равенства, x ln x  получим ln y ln x 1 или, по свойству логарифмов, ln y ln xln x ln x1. Продифференцируем обе части последнего равенства по x: ln y ln xln x ln x 1;  ln y 1 y; ln y 1 y;y ln xln x ln x 1 ln x ln x ln x 1 ln x ln x ln x 1 1 ln x ln x 1 ln x 1 1 2ln x lnx 1 ln x. x x x 1 x x x 1 Таким образом, 1 y 2ln x lnx 1 ln x, y x x x1 откуда получаем 2lnx lnx1 ln x xln x 2lnx lnx1 ln x y y x x x 1 x1 x x x 1 . xln x 2lnx lnx1 ln x Ответ. y x1 x x x 1 . |
