матан. заочники матем 1 семестр по вариантам. Программа, методические указания и контрольные задания 1 семестра для студентов заочной формы обучения всех специальностей
 Скачать 374.69 Kb.
|
Задание 2.2.Привести уравнения второго порядка к каноническому виду. Определить тип кривой, которое оно задает. Построить кривую. а) 9 х2 – 16 у2 +36 х +32 у + 164 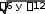= 0;  б) x 3 0.Решение. а) Выделим полные квадраты относительно каждой переменной в левой части уравнения, а свободные члены перенесем в правую часть: 9х2 – 16у2+ 36х+ 32у + 164 = 0; 9 (х2 + 4 х) − 16 (у2 − 2 у) = − 164; 9 ((х2 + 4 х + 4) − 4) − 16 ((у2 − 2 у + 1) − 1) = − 164; 9 (х + 2)2– 36−16 (у − 1)2 +16 = − 164; 9 (х + 2)2 − 16 (у − 1)2 = − 144; 1; 9(x 2)2 16 y 12   144 144 (x 2)2 y 12  1.16 9 Получаем каноническое уравнение гиперболы3 с центром в точке С (−2; 1), мнимой полуосью a = 4, действительной полуосью b = 3 (рис. 2). Для построения гиперболы строим основной прямоугольник с центром С,  3 Каноническое уравнение гиперболы имеет вид (x x0 )2 a2 ( y y0 )2 b2 1 или (x x0 )2 a2 ( y y0 )2 b2 1. сторонами 2a и 2b, параллельными соответственно осям координат Ох и Оу, проводим пунктиром прямые, содержащие диагонали прямоугольника (асимптоты гиперболы). Отмечаем вершины гиперболы (x ; y ± b) = (2; 4) и 0 0 (2; 2) проводим через них две ее ветви, приближающиеся к асимптотам. 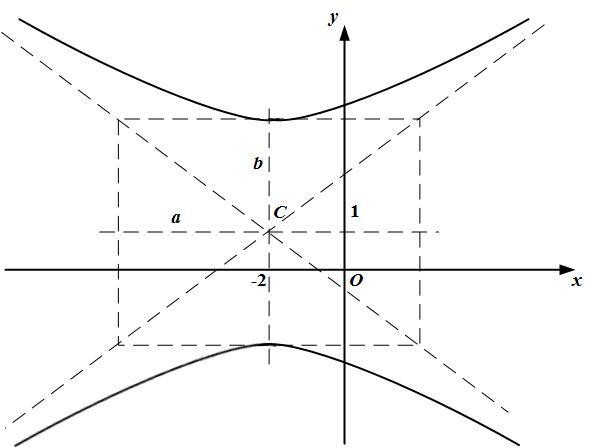 Рисунок 2. Гипербола (x 2)2 y 12 Ответ. Каноническое уравнение: 1.16 9 б) Перенесем выражение, содержащее корень, в правую часть:  x 3 6 y 12.При решении необходимо учесть неотрицательность выражения в левой части равенства (т.к. корень в правой части равенства дает только неотрицательные значения), то есть x − 3 ≥ 0; возведем обе части исходного уравнения в квадрат и вынесем коэффициент при переменной в правой части уравнения: (x − 3)2 = − 6 y + 12; (x − 3)2 = − 6 (y − 2). Учитывая ограничения, получим систему: (x 3)2 6( y 2); x 3. Уравнение (x − 3)2 = − 6 (y − 2) является каноническим уравнением параболы4 с вершиной в точке C(3; 2), осью симметрии x = 3; ветви параболы направлены вниз. С учетом условия x ≥ 3 получаем правую ветвь этой параболы (рис. 3). Параметр 2p = 6 определяет сжатие параболы x2 = y вдоль оси симметрии в 6 раз5. 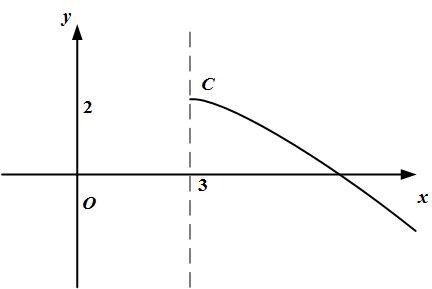 Рисунок 3 Ветвь параболы |