матан. заочники матем 1 семестр по вариантам. Программа, методические указания и контрольные задания 1 семестра для студентов заочной формы обучения всех специальностей
 Скачать 374.69 Kb. Скачать 374.69 Kb.
|
Задание 2.1.Даны координаты трех точек А (9, 4), В (3, 8), С (5, 6).  а) Найти уравнение прямой АН, перпендикулярной прямой ВС в общем, каноническом и параметрическом виде. а) Найти уравнение прямой АН, перпендикулярной прямой ВС в общем, каноническом и параметрическом виде.б) Определить взаимное расположение векторов середина ВС. Решение. а) Дано: А (9, 4), В (3, 8), С (5, 6). Найти: АН, где AH BC. и BC , где О– Для того чтобы написать уравнение прямой АН, нужно сначала ее описать, т.е. определить, что нам о ней известно и записать всю информацию аналитически (с помощью математических выражений). Во-первых, по названию прямой известно, что она проходит через точку А (9, 4). Во-вторых, имеется условие AH BC. 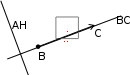 Поскольку на прямой ВС известны координаты точек В и С, то мы можем найти вектор BC , который для прямой ВС называется направляющим1. Рисунок 1. Направляющий вектор прямой ВС  Для того чтобы найти координаты вектора нужно из координат конца Для того чтобы найти координаты вектора нужно из координат концавектора – точки С (5, 6) вычесть соответствующие координаты начала  вектора - точки В(3, 8): 2}. вектора - точки В(3, 8): 2}. 1 Вектор, который параллелен прямой, называется направляющим вектором этой прямой. Можно представить, что направляющий вектор задает «направление» прямой в пространстве. Понятно, что параллельные друг другу прямые будут иметь один и тот же направляющий вектор. Поэтому для описания конкретной прямой указания только направляющего вектора недостаточно. Достаточно указать еще одну точку, через которую проходит эта прямая. Из рис. 1 видно, что BC AH. Вектор, перпендикулярный прямой, называется для нее нормальным. Значит, BC – нормальный вектор прямой АН.  Получили, что искомая прямая АН задана точкой А (9, 4) и нормальным Получили, что искомая прямая АН задана точкой А (9, 4) и нормальнымвектором nAH BC {2; 2}. Известно, что координаты нормального вектора есть коэффициенты перед х и у в общем уравнении прямой2. Пусть общее уравнение прямой АН имеет вид: Ax By C 0. Тогда вместо А и В подставляем координаты нормального вектора nAH {2; 2}. AH : 2x 2y C 0. Чтобы найти значение неизвестного параметра С, используем известную на АН точку А. Точка А лежит на прямой АН тогда и только тогда, когда координаты точки удовлетворяют уравнению прямой. Это значит, что при подстановке координат точки в уравнение прямой мы получим верное равенство. 2 9 2 4 C 0. Откуда следует, что C = − 10. Итак, получили общее уравнение прямой AH : 2x 2y 10 0. Каноническое уравнение прямой на плоскости имеет вид:  x x0 x x0 l1 y y0 ,  l2 l2координаты произвольной точки на этой прямой. Точка на прямой АН у нас известна: А (9, 4).  2На плоскости прямая задается линейным уравнением Такое уравнение называется общим уравнением прямой на плоскости. Для того чтобы найти направляющий вектор, нам нужна еще одна точка прямой АН. Известно, что точка лежит на прямой, если при подстановке координат точки в уравнение прямой мы получаем верное равенство (говорят: «координаты точки удовлетворяют уравнению прямой»). Поскольку мы ищем любую точку прямой, то одну из координат можно выбрать произвольно. Пусть x 2. Подставим его в уравнение прямой АН: 2 2 2y 10 0. Получим y 3. Вторая точка прямой АН найдена: H (2, 3). AH {2 9, 3 4} {7, 7} − направляющий вектор прямой АН.  Поскольку направляющим вектором будут также все векторы, коллинеарные вектору АН , то в качестве направляющего вектора можно взять вектор Поскольку направляющим вектором будут также все векторы, коллинеарные вектору АН , то в качестве направляющего вектора можно взять векторИтак, прямая АН задана точкой А (9, 4) и направляющим вектором  Запишем каноническое уравнение прямой  AH : x 9 AH : x 9 y 4 . 1 1 Распишем два равенства в системе:  x 9 t, 1 или x t 9, y 4 t; y t 4. 1 Получили параметрические уравнения прямой. Ответ. Общее уравнение прямой AH: 2x 2y10 0; каноническое   уравнение прямой AH : x 9 уравнение прямой AH : x 9 y 4 ; параметрические уравнения прямой y t 4, AH : x t 9, где 1 1 t R. б) Дано: В (3, 8), С (5, 6), О – середина ВС.  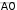 Найти: угол между векторами и BC. Найти: угол между векторами и BC.Определить взаимное расположение векторов угол между ними. и BC, значит – найти Найдем координаты векторов. BC {5 3,6 8} {2, 2}. Так как О – середина ВС, то ее координаты удовлетворяют условию: x х1 х2 , у  у1 у2 ,  где (х , у ), (х , у ) − координаты середина 2 середина 2 1 1 2 2 конечных точек отрезка. Тогда О 3 5 , 8 6 , т. е. О4,7. 2 2 Получим АО {4 9,7 4} {5,3}. 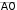 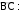 Найдем угол между векторами и Найдем угол между векторами и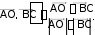 cos cosПо формуле скалярного произведения векторов (через координаты): Находим длины векторов: 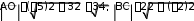 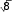 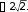 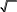 Тогда cos AO, BC 16 417 . Тогда cos AO, BC 16 417 .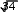 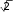 2 17 2 17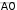 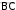 Так как знак косинуса положительный, то векторы и Так как знак косинуса положительный, то векторы и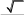 располагаются под острым углом, величина которого равнаarccos 4 17 . располагаются под острым углом, величина которого равнаarccos 4 17 .17 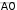 Ответ. Векторы и BC располагаются под острым углом, величина Ответ. Векторы и BC располагаются под острым углом, величинакоторого равна arccos 4 17 . 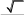 17 17 |

