матан. заочники матем 1 семестр по вариантам. Программа, методические указания и контрольные задания 1 семестра для студентов заочной формы обучения всех специальностей

• Название: Программа, методические указания и контрольные задания 1 семестра для студентов заочной формы обучения всех специальностей
• Анкор: матан
• Дата: 22.01.2021
• Размер: 374.69 Kb.
• Имя файла: заочники матем 1 семестр по вариантам.docx
• Тип: Программа; #170540
• страница: 8 из 23

Задание 3.1.

Вычислить пределы

x²  x  2

_ 2x  3 _^4x

а) lim

x1

; б)

lim

x ^

2

<sup>tg x (x 

2)</sup>^;

в) lim .

^x_ 2x 1 _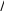

 
Решение.

а) Числитель и знаменатель дроби при x → −1 обращаются в ноль. Значит,

имеем неопределенность вида

 ⁰ _.

_{ 0} _
Для раскрытия неопределенности умножим

числитель и знаменатель на выражение, сопряженное знаменателю, разложив

перед этим числитель на множители:

x²  x  2  (x 1)(x  2) ⁶. Получим

x²  x  2

(x 1)(x 2)_ x 5  2_

(x 1)(x 2)_  2_

lim

 lim

 lim 

x1

x1 _

(x 1)(x  2)_

x 5  2_

 2_

x 5  2_

x1

x  5  4

 lim

x1
x 1

 lim (x  2)



x1

 2_  3 4  12.

Ответ. 12.



⁶ Первый корень получаем из предельного значения x, второй корень определяем по теореме Виета: если приведенное квадратное уравнение x² + px + q = 0 имеет действительные корни, то их сумма равна p, а произведение равно q.

б) При подстановке предельного значения получаем неопределенность

вида _ 0_.

Для раскрытия неопределенности сделаем замену и используем

эквивалентную функцию:

lim

^{tg x (x }

_{2)  } y x  2

^{  lim} <sup>tg( y 

2)  y</sup>  ^

x 2


^ y 0 при x  2^{ y0}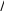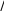

^{  lim} ^tg(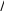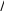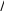

 


 
^{2  y)  y}  ^{  lim} ^{ctg y  y}  ^{  lim y }

y0
 _tg y
Ответ. 1.

y0


^{y0 } y ^
 0 _   lim ^y  1.

 

^{y0 } tg y ^

в) Делением числителя на знаменатель выделим целую часть:

_ 2x 3 2x1


2x1 1

4

Таким образом,

2x 3 _{ 1 } 4

_ 2x  3 _^4x

, lim _{ } 

lim ^1 

_{4 }4x

_ .

2x1 2x1

^x_ 2x 1 _

x_

2x 1 _


При x  основание функции стремится к единице, а показатель к

бесконечности, получили неопределенность вида

^1^{ } . Для раскрытия

 
неопределенности преобразуем функцию так, чтобы использовать второй

замечательный предел:



lim _1 

y_

1 ^{ y}


y



 e. Получим:

4 x 4 x ^2x1 ⁴

lim ^1  ^{4 }  lim ^1  ^{4 }


4 2 x1 _

   

x _



2x 1 _

x _

16 x


2 x1 _{ 2 x1}


2x 1 _


2 x1 _

 lim ^1 

4 _ 4 _


 ^1  ^{4  4}  e при x   ^ 

^{x } 2x1 ^{  } 2x1 ^{ }

_  _{ }  _

16 x

 lim e 2 x1

x

16 x: x



(2 x1): x

lim e

x

16



21 x

lim e

x

16

 e²
 e⁸.

Ответ.

е⁸.