матан. заочники матем 1 семестр по вариантам. Программа, методические указания и контрольные задания 1 семестра для студентов заочной формы обучения всех специальностей

• Название: Программа, методические указания и контрольные задания 1 семестра для студентов заочной формы обучения всех специальностей
• Анкор: матан
• Дата: 22.01.2021
• Размер: 374.69 Kb.
• Имя файла: заочники матем 1 семестр по вариантам.docx
• Тип: Программа; #170540
• страница: 10 из 23

Задание 3.3.

Вычислить предел, используя правило Лопиталя:

lim ^ctg x  ^{1 } .

 
Решение.

^x0 _ x_

Правило Лопиталя используется для раскрытия неопределенностей вида

 ⁰ 

_{ 0} _
или

^{ } . При x 0


 
^ 

получаем неопределенность вида _  _ , поэтому

преобразуем предельную функцию:


lim ^ctg x  ^{1 }  lim ^{ 1}

• 
  1 ^ _{ lim} x tg x_.
  

Получили неопределенность

 ⁰  _и

x0

x^{ x0 } tg x x^

x0

tg x x

_{ 0} _

  _{ }

можем применить правило Лопиталя:

• 
  
  xtgx 
  ^{x  tg x}
  

lim  lim
 lim

_{1 }1


lim 
cos² x
_ cos² x1

x0

tg x x

^x0 ^{tg x  x}^

x0

1


cos² x

 x tg x

^x0 x  sin x  cos x

 lim
sin² x

1

 ^{ 0 }  /применяемправило Лопиталя/   lim

_sin² x_^


x0 _{x }

sin 2x

 ⁰ 




 
^{x0 } x  ¹ sin 2x ^

2 ^ ₂ ^

  lim
2sin xcos x

 

 ^{ 0 }  0.

^x01  ¹  2cos 2x 2

Ответ. 0.

_{ 2} _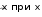

Замечание. Можно упростить вычисления, если использовать эквивалентные функции:

 ¹ 

^1 1 ^

x  tgx

_tg x

 0 _

lim _ctg x 

_  lim _  _  lim

 ^заменить можем только ^ 

x0 _

x_ ^x0 _ tg x x_

x0

tg x x

 

^_множитель взнаменателе^_


1 

 lim ^{x tg x}  /используемправило Лопиталя/  lim



1


cos² x
 lim
cos²

x 1 _

x0 _х<sup>2

x0</sup> 2x

^x0 2x  cos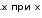² x

_ sin² x x² x

lim

^x0 2x cos² x

 _sin x

 0_   lim

^x0 2x cos² x

  lim

^x0 2cos² x

 0.