матан. заочники матем 1 семестр по вариантам. Программа, методические указания и контрольные задания 1 семестра для студентов заочной формы обучения всех специальностей

• Название: Программа, методические указания и контрольные задания 1 семестра для студентов заочной формы обучения всех специальностей
• Анкор: матан
• Дата: 22.01.2021
• Размер: 374.69 Kb.
• Имя файла: заочники матем 1 семестр по вариантам.docx
• Тип: Программа; #170540
• страница: 13 из 23

Задание 4.2.

M_{2 }1, 2_ и

M_{4 }1,  2_

Найти наибольшее и наименьшее значения функции

z  x²  2xy  4 y 1 в

замкнутой области D, ограниченной прямой

Решение.

Построим область (рис. 7).

y  4

и параболой

(x  2)² 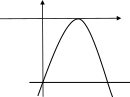  y.

y

x

O

_D 𝑦 𝑥 2 ²

𝑦 4
Рисунок 7. Область

Функция принимает свои наибольшее и наименьшее значения либо во внутренних стационарных точках, либо на границе области.

Найдем все внутренние стационарные точки. Для этого решим систему:

_{ z}'

 0,

_2x  2 y  0,

 x ^ 

y
_z'

 0,

_ 2x  4  0.

Решение этой системы дает координаты первой стационарной точки:

M_{1 }2, 2_ D.

Найдем все стационарные точки на границе области . Граница

составлена из отрезка прямой

y  4

и части параболы

(x 2)²   y

при

0  x  4. Исследуем поведение функции на каждом участке.

Отрезок AB:

y  4, x [0, 4]. Значение функции на отрезке:

 
z  x²  2xy  4 y1  x²  8x17.

y4 _y4

Исследуем на экстремум:

_x²  8x17_'  2x 8  0 

x  4.

Получим вторую стационарную точку границами области.

M_{2 }4, 4_Γ_D.

Она совпала с

Кривая AB:

y (x 2)²,

x [0, 4]. Значение функции на отрезке:

^{z y} ^x2²

 x²  2xy  4 y 1 


 
^y ^x2²

 x²  2x_ x  2_²  4_ x  2_²  1  3x²  8x 15.

Исследуем на экстремум:

_3x²  8x15_'  6x 8  0 

x   ⁴ .

3

Получили точку M^  ⁴ , ^{100 },

не принадлежащую области (она не

3  _{3 9} 

 

удовлетворяет условию 0  x  4).

Вычислим значения функции во всех найденных точках:

• 
  стационарной точке внутри области M_{1 }2, 2_;
  

• 
  стационарной точке на границе области
  

^M₂ ^{4, 4} ^{(в M3 не вычисляем),}

• 
  ^{граничных точках области A}^{0, 4}^{, B}^{4, 4}^.
  

z _M1

 5,

z _{M B}  1 ,

z _А  17 .

2
Выберем наибольшее и наименьшее значения:

absmax z 17, absmin z 1.

D D

Ответ. absmax z 17, absmin z 1.

D D